铝合金弧面节点板冲压成形回弹特性研究

2020-12-04郭小农保文通

同济大学学报（自然科学版） 2020年10期

郭小农，保文通，曾强，徐航

（同济大学土木工程学院，上海200092）

铝合金单层网壳结构具有质量轻、受力合理、造型美观等优点，在国内外得到广泛应用［1］。板式节点是铝合金单层网壳中应用最为广泛的节点形式，其力学性能研究相对完善。郭小农等对铝合金板式节点进行了大量的试验研究和数值模拟［2-3］，并基于理论分析得到了节点承载力计算式和抗弯刚度的四折线模型［4-5］。

但是，上述研究主要针对平面板式节点进行。为满足网壳曲面造型的需求，板式节点上下盖板通常需采用弧面板。弧面节点板是在切割、钻孔而成的平面圆盘的基础上冲压起拱成形的。在冲压成形过程中，板件内外表层材料进入塑性阶段，而中心区仍保持弹性状态，卸载后存在严重的回弹现象。由于铝合金材料延伸率小、屈服强度与弹性模量之比较大，与低强度钢材相比回弹效应更为明显［6-7］，严重影响了节点板的加工精度。目前仅文献［8］对铝合金弧面板式节点的承载性能进行了初步研究，尚未见文献对弧面节点板在冲压过程中的回弹特性展开研究。

本文首先基于有限元软件ABAQUS 建立了铝合金节点板的数值模型，分别采用动态显式分析算法和静态隐式算法模拟冲压成形过程和卸载回弹过程，得到了节点板的回弹量，并通过与实际节点板的加工数据进行对比，验证了模型的有效性。然后对铝合金材料参数、冲压拱度、节点板厚度和半径及螺栓孔位对节点板回弹量的影响进行了参数分析。最后基于理论推导和回归分析得到了节点板回弹量的计算式，并通过计算结果和数值分析结果的对比验证了计算式的准确性。

1 有限元模型的建立与验证

1.1 算法选取

根据节点板成形过程的受荷情况、边界条件和变形特点，可将数值模拟过程分为冲压成形阶段和卸载回弹阶段。相关研究指出，动态显式算法适用于求解有复杂接触关系的成形问题，但在求解回弹问题时准确度较低，计算成本较高；而静态隐式算法虽然在求解成形问题时收敛性较差，但在以弹性恢复变形为主的回弹阶段更容易收敛［9-10］。因此，本文在冲压成形阶段选取ABAQUS/Explicit 进行求解，而在卸载回弹阶段选取ABAQUS/Standard 进行求解［11］。

1.2 模型几何尺寸和材料本构关系

以南昌市某铝网壳工程为背景，建立了铝合金节点板的有限元模型。模型几何尺寸与实际节点板完全相同，见图1。节点板设计拱度为9 mm，所有螺栓孔直径均为10. 5 mm，并在中心开直径为16. 0 mm的应力释放孔。节点板材料为6061‐T6铝合金，采用Ramberg‐Osgood模型描述其本构关系，弹性模量为E=70 GPa，名义屈服强度f0.2=240 MPa，根据Steinhard 建议［12］硬化指数取n=f0.2/10=24。冲压成形设备见图2，节点板放置在上、下模具之间，并通过液压千斤顶加载成形。由于上、下模具均为钢材，其刚度明显大于节点板刚度，建模时可按离散刚体考虑。考虑到节点板几何尺寸和荷载情况的对称性，为提高计算效率，建立了1/2模型，见图3a。

1.3 网格划分与接触关系设置

图1 弧面节点板几何尺寸（单位：mm）Fig. 1 Dimensions of arched gusset plate（unit：mm）

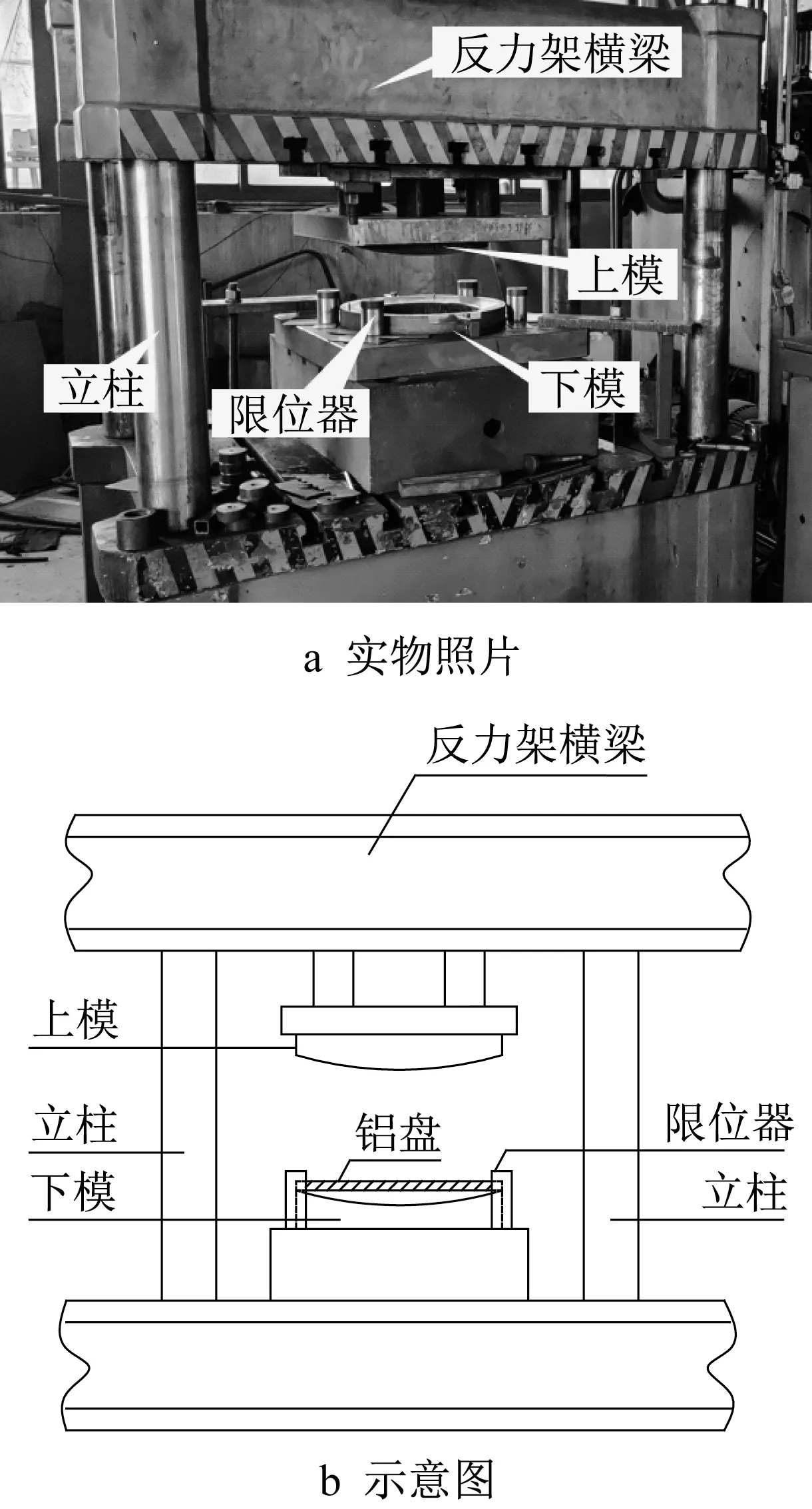
图2 节点板冲压设备Fig. 2 Stamping forming device of gusset plate

采用减缩积分单元C3D8R［13］对节点板进行网格划分，并在板厚方向上划分6 层网格以提高计算精度；对上、下模具采用刚体单元R3D4 进行网格划分，网格尺寸略大于节点板网格尺寸，见图3b。冲压成形过程中，分别在上、下模具与节点板上之间设置表面与表面接触，由于接触面之间的相对滑动较大，故设置为有限滑移；两个接触面法向设置为硬接触，切向设置为罚摩擦，上模具与节点板间摩擦系数取0，下模具与节点板间摩擦系数取0. 1，见图3c、3d。

1.4 约束关系设置与荷载施加

在冲压成形阶段，在Oxz平面内施加对称约束，并设置两个参考点（RP 点）分别与上、下模具耦合，以限制模具的运动，见图4。实际节点板加工过程中多次试压发现，为达到设计拱度9 mm，冲压拱度应取21 mm，故在数值模型中对上模具施加沿z轴负方向相同大小的位移荷载。为确保冲压过程不受惯性效应影响，经多次试算取加载速度为1 m·s−1。

图3 节点板及模具有限元模型Fig. 3 Finite element model of gusset plate and model

在卸载回弹阶段，采用无模法求解回弹问题，即不考虑模具与板材间的脱离过程，而将冲压阶段结束时节点板的几何形状和应力状态作为回弹阶段的初始条件。为防止节点板在回弹过程中出现刚体位移，并最大程度地保证节点板自由变形，在应力释放孔中性面上选取三点设置固定约束，见图5。

图4 成形阶段的约束设置Fig. 4 Constraints in stamping forming stage

图5 回弹阶段的约束设置Fig. 5 Constraints in springback stage

1.5 数值模拟结果与模型验证

节点板冲压成形后及回弹变形后的应力分布及变形情况见图6和图7。冲压成形后，节点板上下表面材料大面积进入了塑性阶段，最大应力达到260 MPa，但中心区仍保持弹性，见图6a；节点板拱度为21. 408 mm，与冲压拱度的误差仅为2. 490%。回弹变形后，在螺栓孔附近存在较大的残余应力，其余区域残余应力均小于80 MPa，见图7a；节点板残余拱度为10. 993 mm，回弹量达到10. 415 mm。节点板回弹前后的竖向变形情况见图8，节点板形状整体基本保持为球面。

图6 冲压成型后节点板的应力分布与变形情况Fig. 6 Stress distribution and deformation of gusset plate after stamping forming

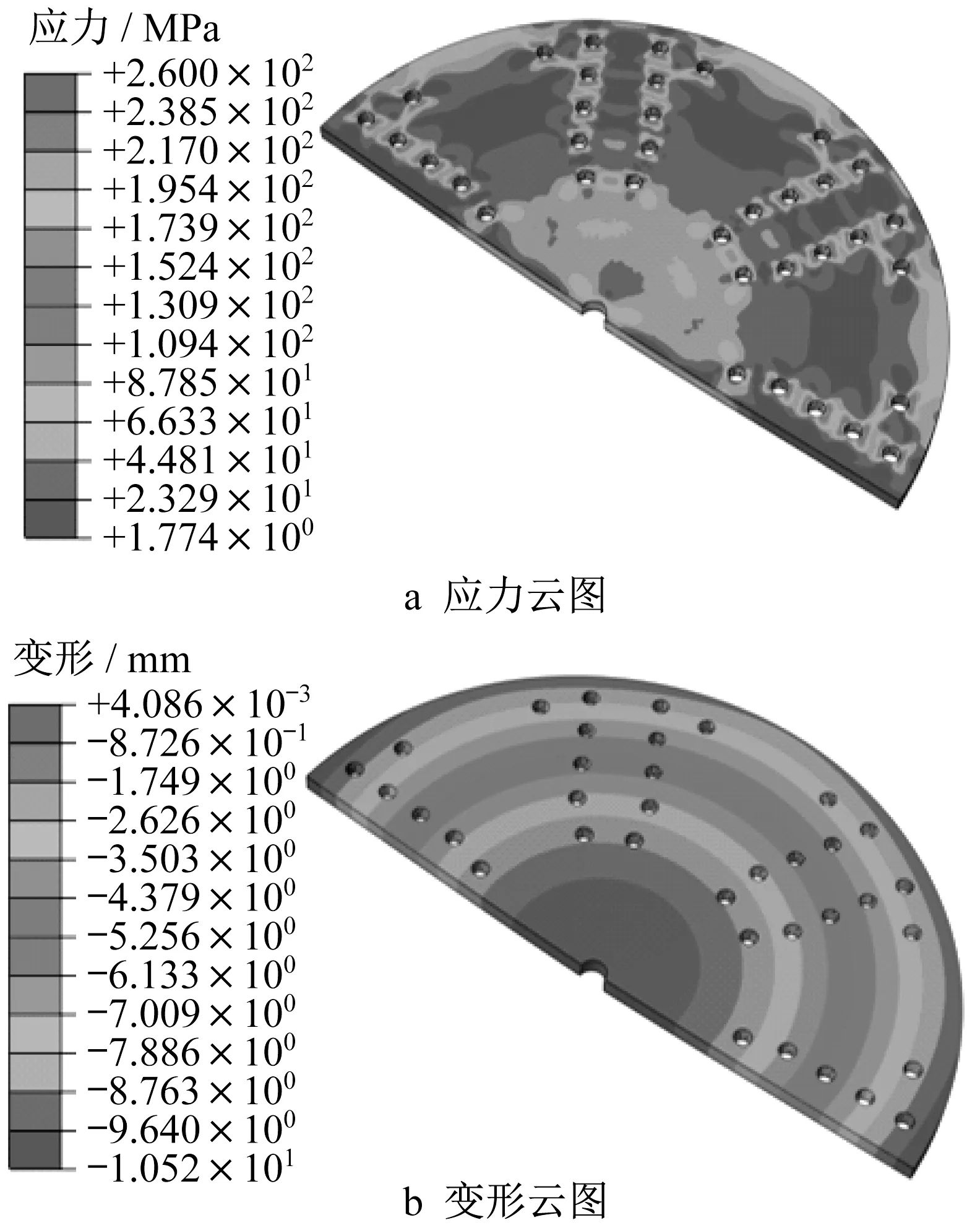
图7 回弹变形后节点板的应力分布与变形情况Fig. 7 Stress distribution and deformation of gusset plate after springback

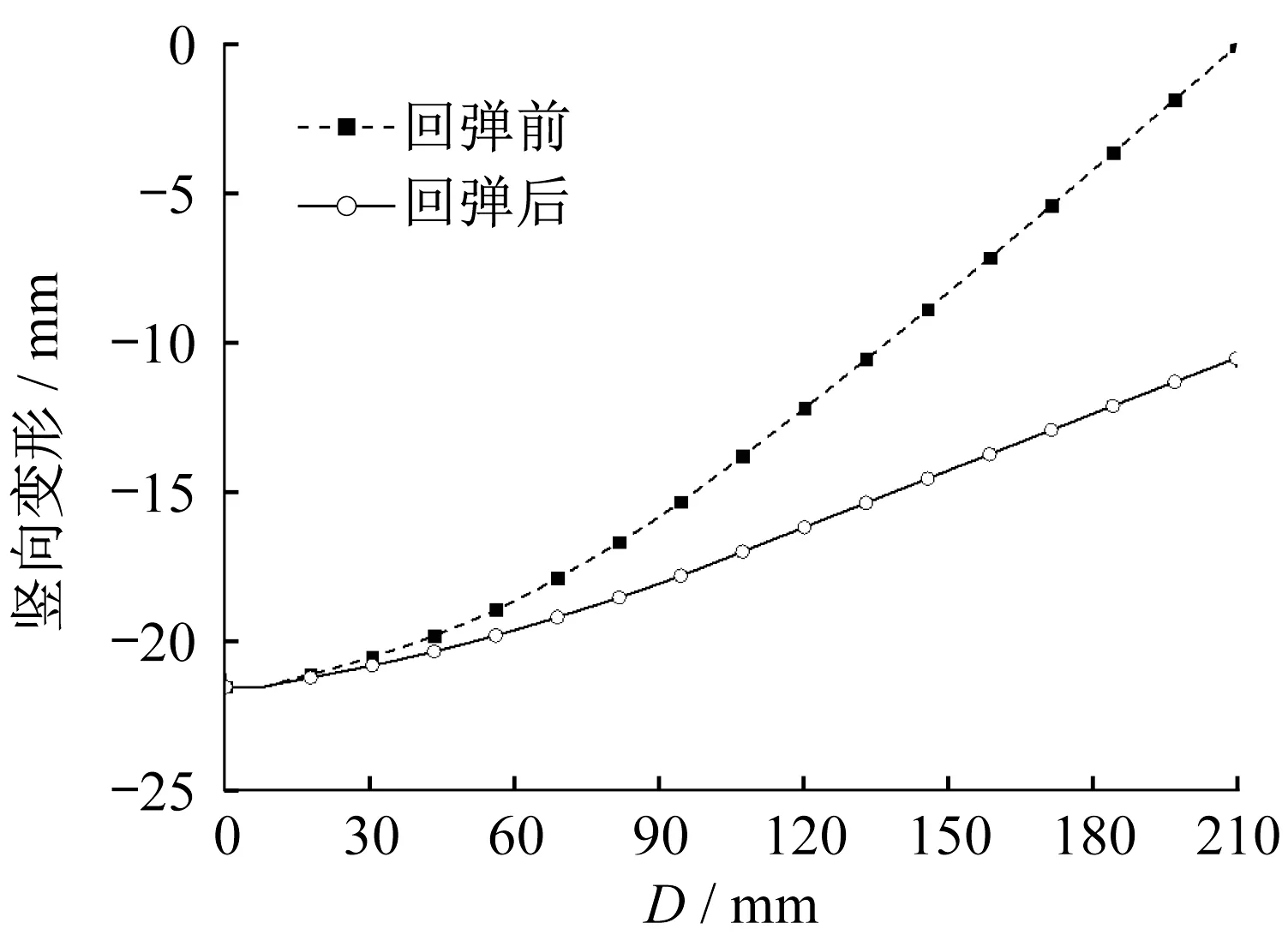
图8 节点板回弹前后的竖向变形情况对比Fig. 8 Shape comparison of gusset plate before and after springback

为验证数值模型的正确性，采用游标卡尺测量实际节点板中心（见图9）的残余拱度，同时采用三维扫描仪测量得到节点板回弹后的最终形状。实测结果表明，节点板中心最终残余拱度平均值为9. 50 mm，回弹量为11. 50 mm，数值模拟结果与实测结果的误差仅为−9. 345%，说明所建立的有限元模型能准确预测节点板的回弹量。

图9 节点板拱度测量Fig. 9 Measurement of gusset plate arch

2 节点板回弹量的影响参数分析

节点板成形过程中，铝合金材料参数、冲压拱度、节点板厚度和半径及螺栓孔的布置等因素都对回弹量有较大的影响。为确定各项参数对节点板回弹量的影响，建立了5 个系列共计36 个模型进行参数分析，数值模型的详细信息见表1。表中，r、t分别为节点板半径及厚度，h为冲压拱度，db为螺栓孔直径，ab为节点板开孔面积率，SFE为数值分析得到的节点板回弹量，SEq为节点板回弹量，re为拟合结果与数值结果的相对误差。表中，b系列模型选取了工程中常见的4 种构造，每种构造取10. 5 mm 和12. 5 mm两种螺栓孔直径，并增加无螺栓孔圆板和螺栓群中心线夹角不均匀的节点板，见图10。

图10 节点板构造类型Fig. 10 Construction types of gusset plate

2.1 铝合金材料参数对回弹量的影响

表1 中m 系列数值模型研究了铝合金材料参数［14］对节点板回弹量的影响，其中不同牌号铝合金的材料特性如表2所示。节点板回弹前后的竖向变形见图11。图中，D为距节点板中心的距离。数值模拟结果表明，材料参数对冲压成形过程的影响较小，所有模型回弹前的形状基本保持一致；在回弹变形过程中，节点板回弹量随着材料弹性模量E和名义屈服强度f0.2的提高而增大。显然，热处理状态为T4 的合金由于比T6 状态的合金软，因此其回弹也较小。

2.2 冲压拱度对回弹量的影响

表1 中h 系列数值模型研究了冲压拱度对节点板回弹量的影响，节点板回弹前后的竖向变形和回弹量分别见图12和图13。数值模拟结果表明，当冲压拱度较小时，节点板大部分材料基本保持弹性状态，回弹量随冲压拱度的增大而增大；当冲压拱度大于17 mm时，随着冲压拱度的增大，节点板中性面附近弹性区域逐渐减少，导致回弹量逐渐减小。值得注意的是，在冲压拱度增大的过程中，节点板回弹量与冲压拱度的比值始终保持降低趋势，说明节点板塑性变形发展程度逐渐提高。

表1 模型信息汇总表Tab. 1 Summary of model information

表2 材料参数Tab. 2 Material properties

2.3 节点板厚度对回弹量的影响

表1 中t 系列数值模型研究了节点板厚度对回弹量的影响，节点板回弹前后的竖向变形和回弹量分别见图14和图15。当其他参数保持不变时，节点板回弹量随着厚度的增大而减小，且回弹量减小的趋势逐渐趋于平缓。主要原因是在冲压拱度相同的情况下，节点板厚度越大，变形后板件上下表面的应变越大、材料的塑性发展程度越高，卸载回弹阶段弹性恢复变形也越小。

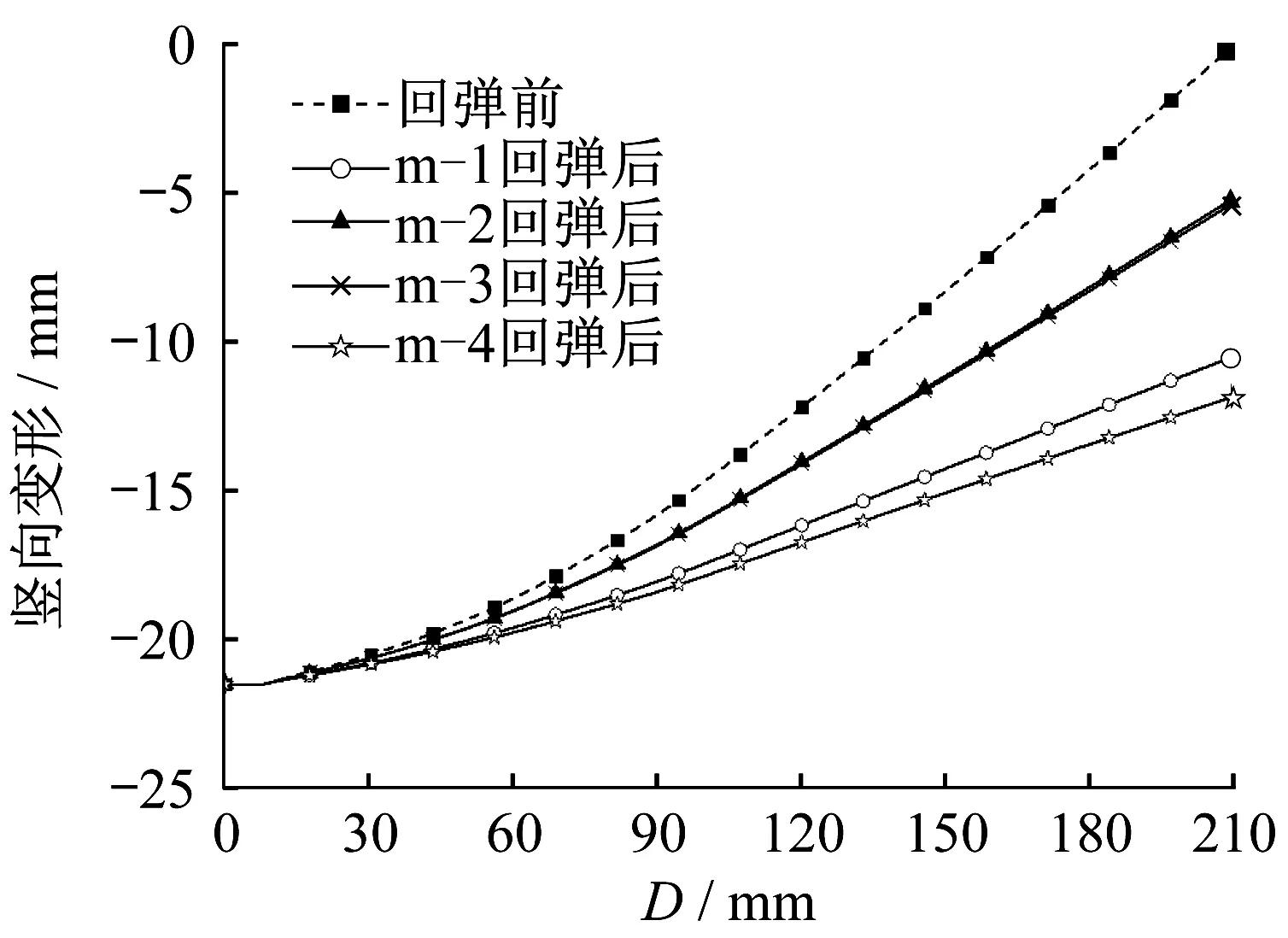
图11 m系模型回弹前后的竖向变形Fig. 11 Vertical deformation of group m before and after springback

图12 h系模型回弹前后的竖向变形Fig. 12 Vertical deformation of group h before and after springback

图13 h系模型的回弹量Fig. 13 Springback value of group h

2.4 节点板半径对回弹量的影响

表1 中的r 系列数值模型研究了节点板半径对回弹量的影响，节点板回弹前后的竖向变形和回弹量分别见图16和图17。当其他参数保持不变时，节点板回弹量随着半径的增大而增大，且回弹量增大的趋势基本保持线性。主要原因是节点板半径越大，其弯曲变形能力越强，在达到相同冲压拱度时弹性变形占总变形的比例越高，卸载后弹性恢复变形也越大。

图14 t系模型回弹前后的竖向变形Fig. 14 Vertical deformation of group t before and after springback

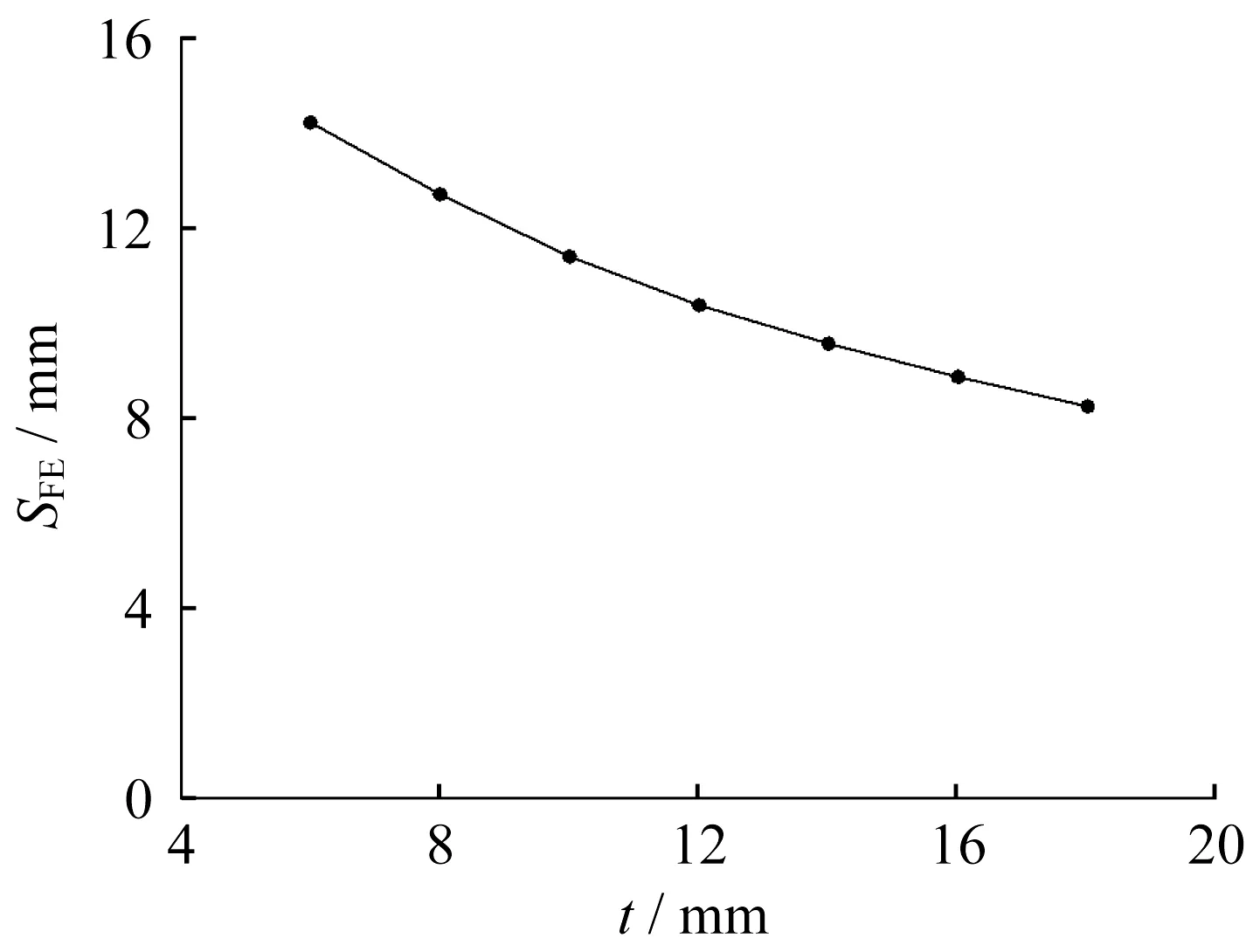
图15 t系模型的回弹量Fig. 15 Springback value of group t

图16 r系模型回弹前后的竖向变形Fig. 16 Vertical deformation of group r before and after springback

2.5 螺栓孔的布置和开孔面积对回弹量的影响

表1 中的b 系列数值模型研究了螺栓孔的布置和开孔面积对回弹量的影响。对比模型b‐1和b‐10，构造相同时，螺栓群中心线夹角是否均匀对节点板回弹量的影响可忽略不计。构造1和构造2模型、构造3 和构造4 模型分别用于6 杆和4 杆两类节点，当开孔面积率相近时，6杆节点板的回弹量稍大于4杆节点板的回弹量，螺栓孔对回弹量有一定影响；但对于同类型节点板，回弹量随着开孔面积率的增加而减少，且基本保持线性关系，见图18。

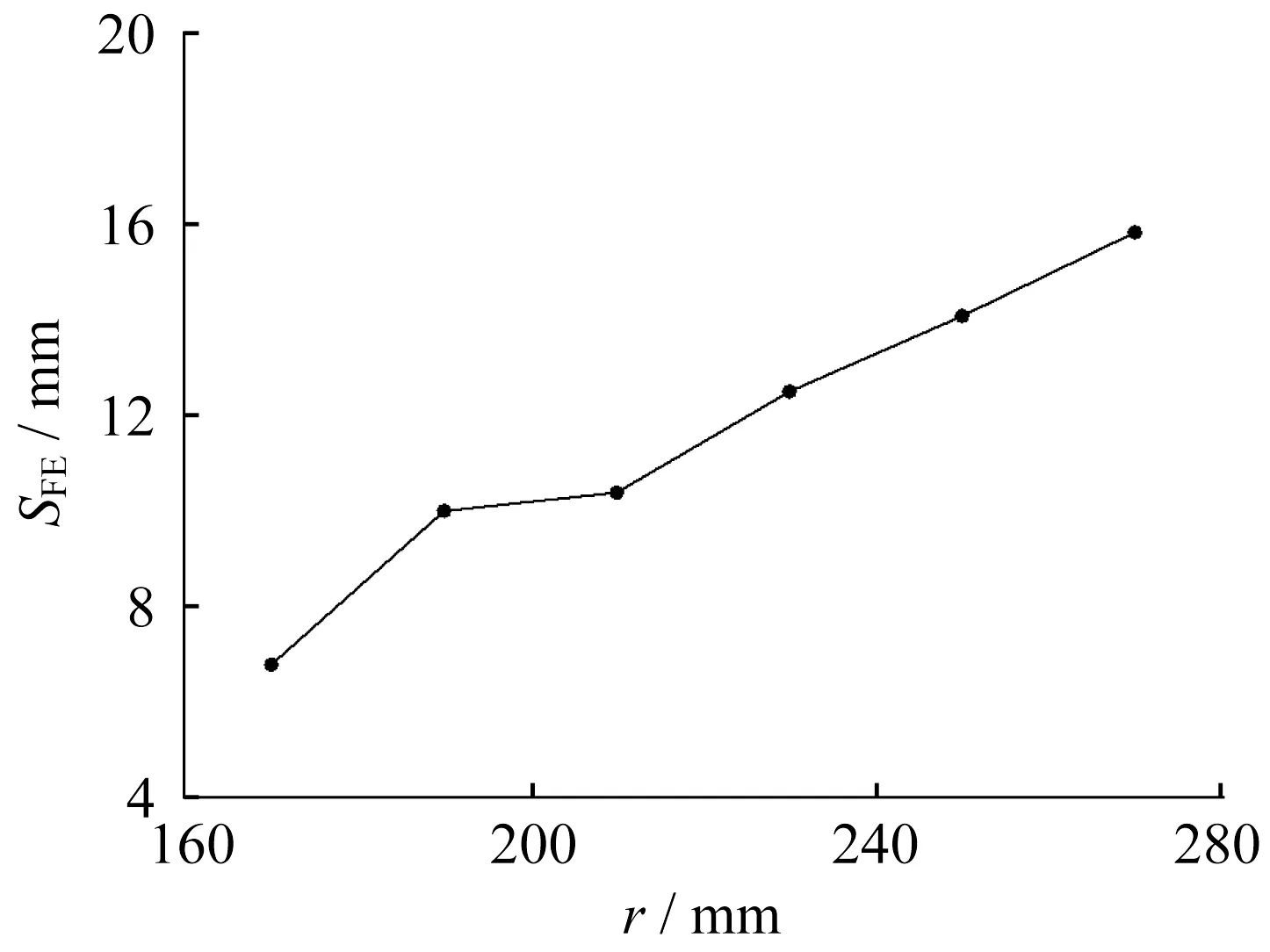
图17 r系模型的回弹量Fig. 17 Springback value of group r

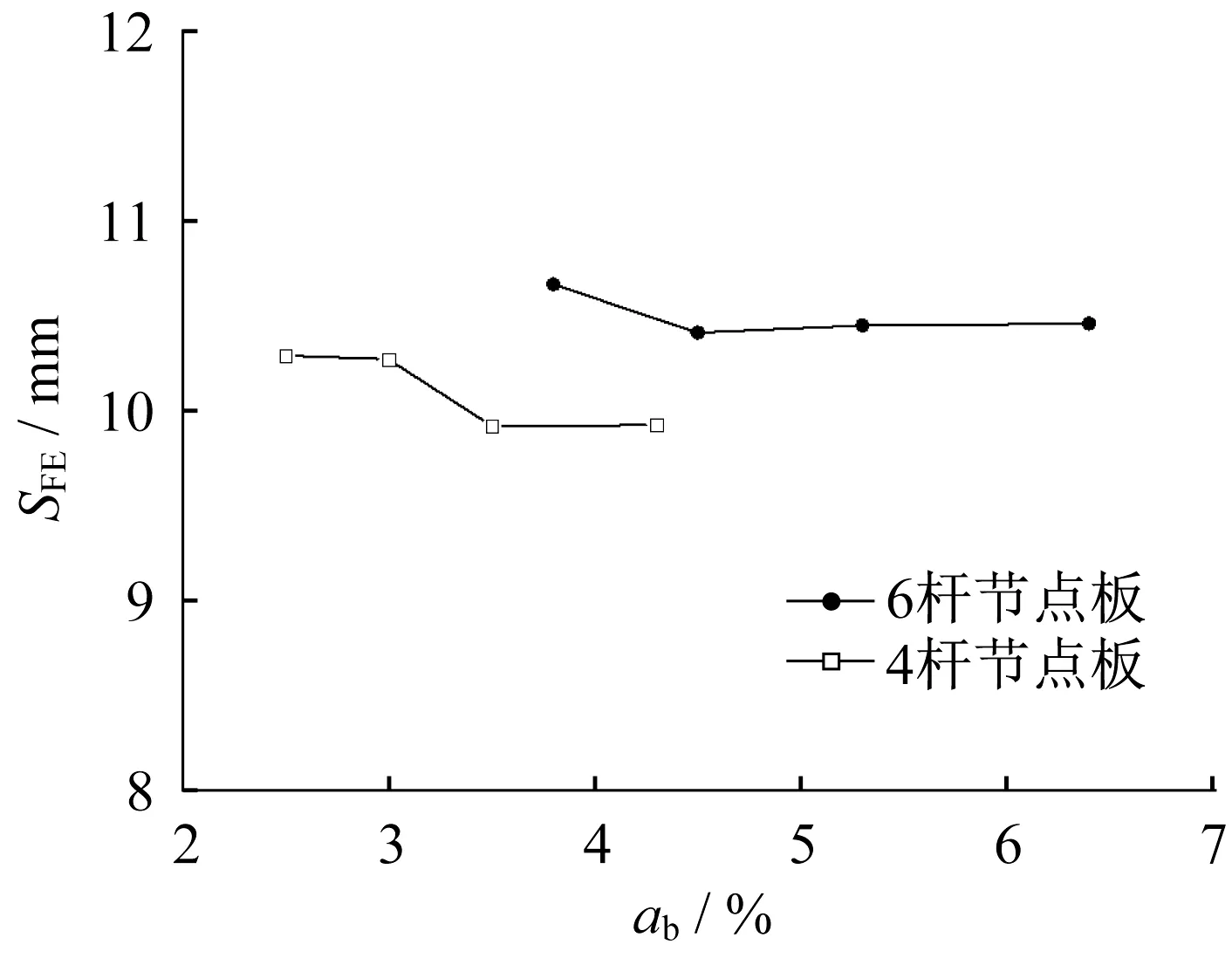
图18 b系模型的回弹量Fig. 18 Springback value of group b

3 弧形节点板回弹量计算式

3.1 回弹量计算式理论推导

由于铝合金节点板的开孔面积率一般在10%以下，可先忽略螺栓孔对节点板回弹量的影响，取无孔圆板进行分析。同时，铝合金材料本构关系按理想弹塑性考虑，并假定节点板在冲压成形后、回弹变形前与模具完全贴合（即节点板为一球面），节点板的形状见图19。

由图19 可得，节点板半径对应的圆心角ψ及表面的径向应变εr为

式中：R0为模具曲率半径。

由于节点板几何尺寸和荷载的对称性，其表面的环向应变εθ应等于径向应变εr，即

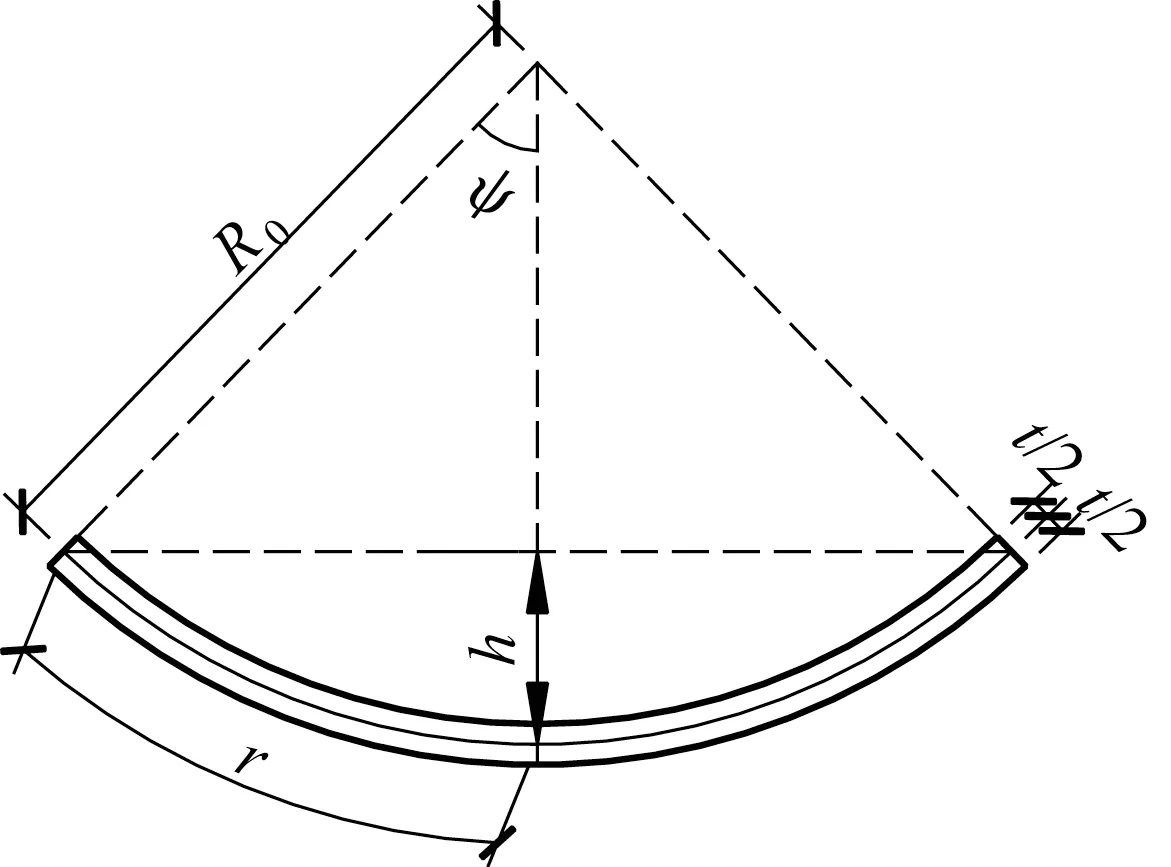
图19 冲压成形后节点板几何形状Fig. 19 Shape of gusset plate after stamping forming

根据弯曲薄板的小挠度理论［15］，可得

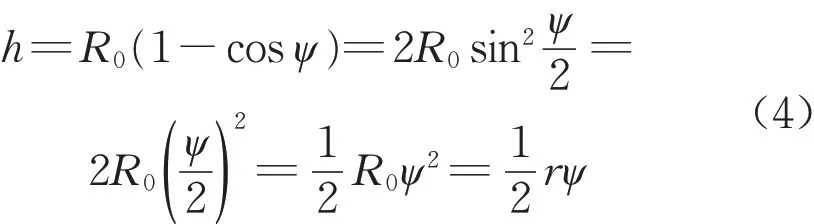
式中：h为冲压拱度。

将式（4）代入式（3）中，可得

冲压成形后节点板沿厚度方向的应变、应力分布见图20a、21a。其中，β为节点板弹性核高度系数，σe为材料保持弹性时对应的应力。假设板内垂直于板面的正应力可忽略不计，即节点板表面上任意一点均处于平面应力状态，则σe可由如下广义虎克定律和第四强度准则求得：

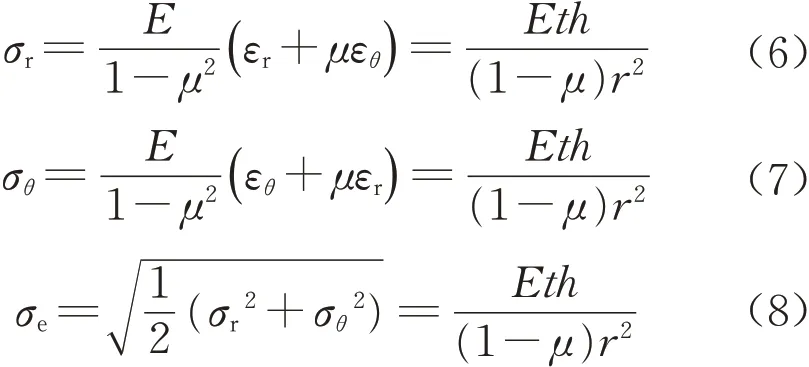
式（6）～（7）中：σr、σθ分别为节点板的径向应力和环向应力；μ为节点板泊松比。

则根据比例关系可得弹性核高度系数β为

回弹过程中，节点板弹性恢复变形对应的应变和应力均沿厚度方向线性变化［16］，见图20b、21b。回弹结束后的应变和应力即为冲压成形后与回弹过程中对应的应变和应力的差值，如图20c、21c所示。其中α为回弹系数，其值等于回弹量与冲压拱度的比值。根据回弹前和回弹阶段板中应力分布的力矩平衡关系，可得

图20 沿厚度方向应变分布Fig. 20 Distribution of strain along the thickness direction

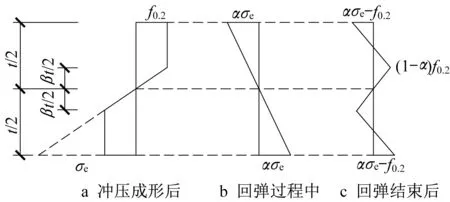
图21 沿厚度方向应力分布Fig. 21 Distribution of stress along the thickness directionn

由于在推导过程中对冲压变形后的节点板形状及材料本构关系进行了简化，且未考虑开孔对回弹量的影响，可保留式（12）的形式，并引入待拟合系数k1、k2，以及开孔面积率修正系数γ对回弹量计算式进行修正，即

3.2 回弹量计算式系数回归分析

根据参数分析结果，选取b 系列模型的计算结果对开孔面积率修正系数γ进行回归，可分别对4杆节点板和6杆节点板采用不同的开孔面积率修正系数，回归结果如下：

在扣除开孔面积率对节点板回弹量的影响后，选取除b系列模型外的其他模型对系数k1、k2进行回归。需要指出的是，由于模型h‐1、h‐2 和h‐3 的冲压拱度较小，回弹后节点板接近平板，故其计算结果不参与回归分析。最终得到的节点板回弹量计算式为

3.3 回弹量计算式验证

采用式（14）、（15）计算表1 中节点板模型的回弹量，并与数值分析结果进行对比，见表1。从表1可以看出，计算结果SEq与数值分析结果SFE吻合良好，绝大多数误差在±10% 以内，最大误差为18. 87%。当板厚t≤8 mm 或t≥18 mm 及冲压拱度h≥25 mm时，计算结果误差较大，其主要原因是当板厚和冲压拱度超过一定范围后，节点板与上下模具在冲压成型过程中并不完全贴合，冲压成形后节点板的整体形状不再保持为球面，此时拟合公式将不再适用。