基于再生骨料方位的模型再生混凝土损伤演化分析

刘 琼，肖建庄，2，郅 晓，王肇嘉

（1. 同济大学土木工程学院，上海200092；2. 同济大学工程结构服役性能演化与控制教育部重点实验室，上海200092；3. 中国建材集团有限公司，北京100036；4.北京金隅集团股份有限公司，北京100031）

近年来，我国城市化进程速度持续加快，每年拆除旧建筑面积达2 亿m2，产生的建筑废弃物超过20亿t［1-2］，其中废旧混凝土占40%以上，但是其资源化利用比例仍然不高。关于再生粗骨料混凝土的基本性能研究已经开展不少，并取得阶段性成果，证明再生骨料的存在会造成再生混凝土力学性能劣化，且随再生骨料掺量增加劣化程度也增加［3-4］。相关的技术规程、技术标准已经颁布并实施，包括国家标准《混凝土用再生粗骨料：GB/T 25177—2011》［5］等。

但是，混凝土受力作用下损伤演化规律难以捕捉，将混凝土模型化即是将混凝土二维化，从而能清晰地看到混凝土内骨料相和硬化水泥砂浆相之间的比例和位置关系，以及在受力破坏过程中的裂缝开展过程［6-8］。基于此，肖建庄等［9-10］提出了模型再生混凝土的方法，首先取天然石材制取圆柱形模型骨料，然后在圆柱表面浇筑圆环形老砂浆，最后将9个模型再生骨料均匀排布，并在周围浇筑新砂浆形成板式试件，制得模型再生混凝土板式试件厚度30 mm。试验结果显示，模型再生混凝土试件受压破坏时，总是在较为薄弱的界面区产生裂缝，然后向老砂浆扩展，最后延伸到新砂浆；另外，对于老砂浆强度低于新砂浆的情况，裂缝总是在天然骨料和老砂浆之间的老界面区开展，而对于老砂浆强度高于新砂浆的情形，裂缝总是在老砂浆和新砂浆之间的新界面区产生。李文贵等［11］利用有限元模拟，进一步研究了不同老砂浆厚度对模型再生混凝土强度、弹性模量和峰值应变的影响，结果显示，随老砂浆厚度增加，模型再生混凝土的初始弹性模量和强度均减小，峰值应变变化不太明显；相对于老砂浆，新砂浆强度增加对整个模型再生混凝土有更大影响。

上述模型再生混凝土的研究将骨料简化为圆形，而真实的骨料则有棱角，为了研究骨料棱角以及这些棱角的方位对再生混凝土力学性能和破坏规律的影响，本研究利用正方形模型天然骨料和模型再生骨料制作了模型普通混凝土和模型再生混凝土，并将模型骨料按照不同方位放置。在对试件进行单轴受压破坏试验过程中，用数字图像相关技术采集其应变集中状态和裂缝开展过程，并配合有限元数值模拟对比分析应变集中情况，开展基于不同再生骨料方位的再生混凝土损伤演化规律研究。

1 试验设计

1.1 模型再生混凝土设计

选取厚度20 mm 的天然石材板，切割取得正方形天然骨料，边长35 mm 的正方形骨料作为普通混凝土骨料；另外，切割边长25 mm 正方形骨料，然后在该骨料外侧浇筑5 mm厚的砂浆层，构成模型再生骨料。模型普通混凝土是由正方形骨料和水泥砂浆浇筑而成的板式试件，试件外形尺寸为100 mm×100 mm×20 mm。类似的由模型再生骨料制作的板式试件为模型再生混凝土。考虑骨料3 个放置方位：骨料边界与试件边界分别成0°、45°和22. 5°角，如图1 所示，浇筑完成的模型普通混凝土和模型再生混凝土试件也在图1中展示。

砂浆采用的原材料包括：P. O. 42. 5 水泥，自来水和河砂；河砂粒径小于2. 36 mm。作为再生骨料中的老砂浆的质量配合比：水泥∶水∶砂为1. 0∶0. 5∶3. 0；新砂浆的质量配合比：水泥∶水∶砂为1. 0∶0. 6∶3. 0。

图1 试件及尺寸Fig. 1 Specimens and sizes

1.2 材料基本性能

为了准确把握各相材料基本性能，取天然石材，切取3 个40 mm×40 mm×160 mm 的棱柱体试件，另外，浇筑新、老砂浆试块40 mm×40 mm×160 mm各3 个。在绝干状态下分别测试天然石材、新砂浆和老砂浆的密度，如表1中所示。然后将3个模型混凝土试块在电子万能试验机上测试抗压强度、弹性模量和泊松比，取平均值得到材料的基本力学性能也在表1中显示。由表1可以看出，天然骨料的密度最高，为2 560 kg·m−3，新、老砂浆的密度约为2 200 kg·m−3。天然石材的弹性模量明显高于其他材料，约为砂浆材料的3 倍，这是造成天然骨料和硬化砂浆间应力集中的原因之一。对比几种材料的抗压强度，不难看出，其规律与弹性模量相似；几种材料的泊松比较接近，而且天然石材的泊松比较新、老砂浆稍低。

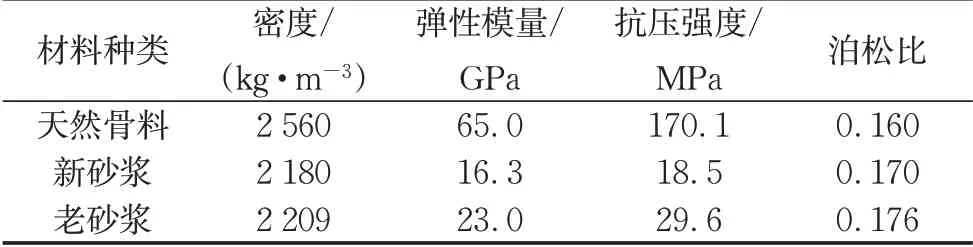
表1 各相材料物理性能Tab. 1 Physical properties of each phase

1.3 数字图像相关

数字图像相关（DIC）技术是一种非接触的无损变形测试方法。在对试件加载过程中，针对试件表面的散斑采集数字图像，并对比这些散斑斑点相对位置的变化，可计算出试件表面的位移场，进一步分析得到应变分布场，从而得到应变集中、裂缝孕育开展的过程。在试件前表面制作散斑斑点大小约0. 8 mm，并在待测区域表面粘贴标尺用于数字图像相关计算分析中的标定。用于图像采集系统的工业相机（型号JHSM300f）的分辨率为2 048×1 536像素，可视范围约为150 mm×120 mm，整个试件表面均在可视范围内，分辨率可达0. 07 mm·像素−1。图像采集频率为5 s·次−1。数字图像相关的应变场云图质量受散斑大小、散斑密度、开裂位置、破坏模式等因素影响，选择应变场云图质量较佳的一个试块进行结果分析与讨论。

2 试验结果与讨论

2.1 力学性能

加载过程中测得每个试件的峰值荷载，除以试件的断面面积100 mm×20 mm，即得到试件的抗压强度，如表2所示。首先可以看出，除了骨料方位0°的模型普通混凝土和模型再生混凝土抗压强度相等，其他两种骨料方位的情况，模型普通混凝土强度均高于模型再生混凝土。3 种骨料方位的模型普通混凝土试件的强度平均值相对模型再生混凝土强度平均值高8%。另外，对于模型普通混凝土和模型再生混凝土，骨料方位22. 5°时，都表现出最高的抗压强度；其次是骨料方位为0°；骨料方位45°的情况其抗压强度最低，可能的原因是，此时骨料上下两个尖端能造成最为明显的应力集中，从而造成裂缝过早出现且强度降低。

表2 模型混凝土力学性能Tab. 2 Mechanical properties of modeled concrete

采用加载曲线上升段中峰值荷载20% 和70%的点，结合实测位移变化，可以计算得到试件的应变，进而计算得到割线模量，如表2 所示，该割线模量可以表征试件对压力作用的变形响应程度。模型普通混凝土的割线模量均高于模型再生混凝土，3个不同骨料方位的模型普通混凝土的割线模量分别较对应的模型再生混凝土高10. 0%、8. 5%和11. 0%。从分相的角度，骨料的方向改变并不造成各相含量的变化。对于模型普通混凝土，骨料相和砂浆相的含量分别为12. 25%和87. 75%；对于模型再生混凝土，骨料相、老砂浆相和新砂浆相的含量分别为6. 25%、6. 00%和87. 75%。对比3种骨料方位的模型普通混凝土和模型再生混凝土的割线模量，可以发现，22. 5°骨料的情况割线模量最高，其次是骨料方位为0°的情况，骨料方位45°的情形其割线模量最低。这说明，骨料方位影响混凝土和再生混凝土的割线模量，如果将混凝土中各相材料等效为不同串联、并联关系的一系列弹簧，那么改变骨料方位意味着改变串联、并联关系，会造成混凝土割线模量的变化；另外，不同的骨料方位可能影响界面区性能，并最终影响混凝土整体的割线模量［12-13］。

2.2 模型普通混凝土破坏过程分析

2. 2. 1 骨料方位0°

对于正方形石材骨料制作的模型普通混凝土试件，当骨料水平方向放置，即骨料左右两侧边与试件左右两侧边平行，并且与受压荷载方向平行。试件的破坏形态为受压作用下的劈裂破坏，而且明显沿界面过渡区，因为界面区黏结薄弱，容易发生开裂。当加载至80%的峰值荷载时，骨料两侧界面过渡区处水平方向应变云图出现清晰的应变集中现象，如图2a 所示。随着荷载的增加，应变集中越来越明显，当骨料两侧界面过渡区水平方向应变达0. 004 2时，如图2b 所示，荷载接近峰值，随后，裂缝沿该位置展开，荷载随之迅速下降。

图2 骨料方位0°的模型普通混凝土破坏过程Fig. 2 Failure process of modeled concrete of 0° aggregate

2. 2. 2 骨料方位22. 5°

将骨料转动22. 5°放置，则加载时骨料左右两侧边与加载方向成22. 5°角，加载到一定程度时骨料上下两顶点到左右两侧边出现应变集中，当加载到80% 的峰值荷载时，应变集中值达到0. 003 8，如图3a 所示。继续加载，则在骨料两侧界面区的应变集中进一步加剧，而且，根据图3b，至峰值荷载时，可能开裂的位置在其他区域也有孕育和发展，最大应变集中值发生在骨料左侧界面区的骨料尖端处，其值为0. 012 7，裂缝从该位置张开，试件也随即达到峰值荷载。

图3 骨料方位22.5°的模型普通混凝土破坏过程Fig. 3 Failure process of modeled concrete of 22.5° aggregate

2. 2. 3 骨料方位45°

将模型骨料按照基于水平方向转动45°，制得模型普通混凝土，其上下两个尖端极有可能成为破坏的起始点，通过试验也证明了这一点，加载至峰值荷载的80%时，模型骨料上部尖端处应变集中值达到0. 004 6，下部尖端也出现应变集中，但是程度相对稍轻，如图4a所示。随着压力荷载的增加，骨料下部尖端处的应变集中情况发育更快，临近峰值荷载时，该部位的水平方向应变值达到0. 008 8，见图4b，随即试件从该处开裂，外力荷载下降。

2.3 模型再生混凝土破坏过程分析

2. 3. 1 骨料方位0°

图4 骨料方位45°的模型普通混凝土破坏过程Fig. 4 Failure process of modeled concrete of 45° aggregate

当模型再生骨料水平放置时，模型再生混凝土的破坏形式也是沿骨料左右两侧界面区的劈裂破坏，对于再生骨料，界面区分为新、老两层，包括天然骨料与老砂浆之间的老界面区，老砂浆和新砂浆之间的新界面区。根据图5a中应变集中的位置，可知新界面区的应变集中程度更加明显，这可能是因为，该模型再生混凝土的新砂浆强度较低，则新界面区的黏结力也更低，所以劈裂裂缝更容易首先在该部位出现。但是随着压力荷载的增加，应变集中现象在新老界面区都迅速发展，至临近破坏时，应变集中值达到0. 007 8，见图5b。

图5 骨料方位0°的模型再生混凝土破坏过程Fig. 5 Failure process of modeled recycled concrete of 0° aggregate

2. 3. 2 骨料方位22. 5°

当骨料方位为22. 5°时，应变集中也首先发生在再生骨料左右两侧，根据图6a所示，新界面区的应变集中更明显。随荷载增加，新老界面区乃至整个老砂浆区域都呈现应变集中状态，而且，可能开裂的区域向上和向下进一步延伸，如图6b所示，而且，在试件其他区域的新砂浆也有裂缝孕育。应变集中最大值在临近破坏时达到0. 016 1，发生在再生骨料左右两侧界面区的上下两个尖端处。

2. 3. 3 骨料方位45°

模型再生骨料方位为45°放置时，应变集中也首先在骨料上下两个尖端出现，荷载施加到峰值荷载80% 时，模型再生骨料上部尖端处的应变集中值达到0. 003 5，见图7a。随荷载增加，应变集中沿老砂浆区域及老砂浆左右两侧的新老界面区发展，呈现如图7b所示的应变集中云图，最大值发生在上下尖端，其值为0. 010 3 时裂缝突然开裂，裂缝在新老界面区均有发生。

2.4 有限元仿真模拟

采用ANSYS 有限元软件，Plan42 单元，天然骨料和新老砂浆的力学参数取值见表1所示。本构模型采用理想弹塑性模型、屈服准则采用Drucker‐Prager 模型，其中，黏聚力取抗压强度的1/10，剪切角取50°［14］。施加80%峰值荷载，采用完全牛顿‐拉夫森迭代法进行非线性求解。

图6 骨料方位22.5°的模型再生混凝土破坏过程Fig. 6 Failure process of modeled recycled concrete of 22.5° aggregate

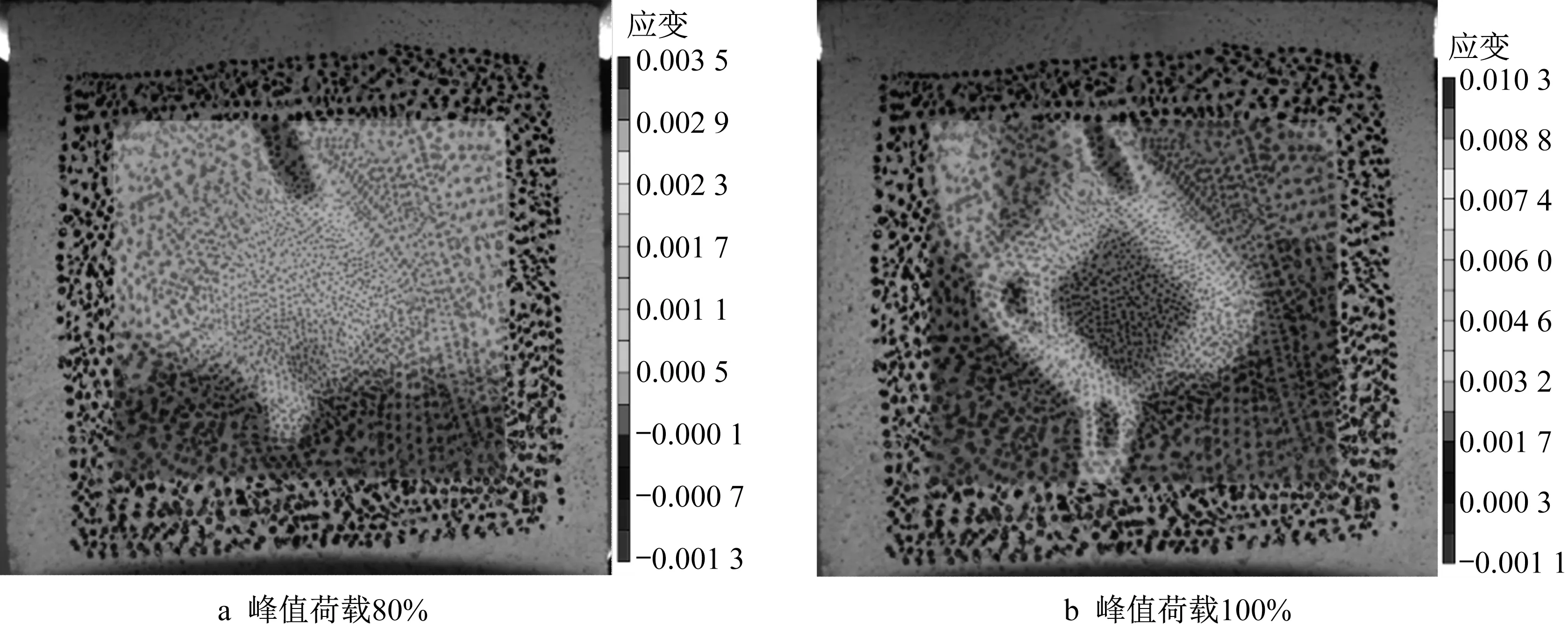
图7 骨料方位45°的模型再生混凝土破坏过程Fig. 7 Failure process of modeled recycled concrete of 45° aggregate

模型普通混凝土试件水平方向应变如图8 所示。由图可以看出，当模型骨料水平方向放置时，骨料上部和下部的砂浆出现较大的水平方向拉应变，最大拉应变达0. 003 1；当模型骨料转动22. 5°放置时，则骨料上下尖端处的砂浆出现明显的应变集中现象，应变值达到0. 003 7；当模型骨料按照45°角放置时，其上下尖端处应变集中程度更加明显，应变值达到0. 004 6。

模型再生混凝土的水平方向应变云图如图9所示。首先可以看出，由于老砂浆的存在，应变集中程度相对模型普通混凝土有不同程度减轻。对于3种不同的骨料放置方向，模型再生混凝土的最大应变值分别为0. 002 7、0. 002 8、0. 003 3。对比分析可以看出，模型再生混凝土的应变集中程度相对模型普通混凝土的分别减轻15%、32%和39%。

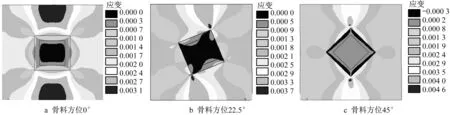
图8 模型普通混凝土X方向应变云图Fig. 8 Strain contour along X of modeled concrete

图9 模型再生混凝土X方向应变云图Fig. 9 Strain contour along X of modeled recycled concrete

2.5 讨论

为了便于对比分析模型普通混凝土和模型再生混凝土破坏过程中应变集中的变化情况，以及进行试验结果与有限元模拟结果的对比分析，将试验过程中80% 峰值荷载时的应变集中值和达到峰值荷载时的应变集中值汇总于表3，并将有限元模拟得到的80% 峰值荷载时的应变集中值也展示在表3 中。可以看出，除了骨料放置方向为0°时，有限元模拟的结果与试验结果比较吻合。骨料放置方向为0°时，有限元模拟得到的应变最大值发生在骨料上下两侧的砂浆区域，而试验得到的应变最大值发生在骨料左右两侧与砂浆的界面处。对于另外两种骨料方位的情况，有限元模拟得到的应变集中位置与试验得到的应变集中位置吻合，其应变值也比较接近。

对比模型普通混凝土和模型再生混凝土，可以发现在80%峰值荷载时，模型再生混凝土应变集中程度较轻。但是在开裂前应变集中值更高，这可能是因为老砂浆强度和弹性模量较新砂浆高。老砂浆的存在削弱了天然骨料和新砂浆之间弹性模量的巨大差异，从而削弱了应变集中造成的开裂风险，使应变集中发育到更高的程度才发生开裂［15-16］。

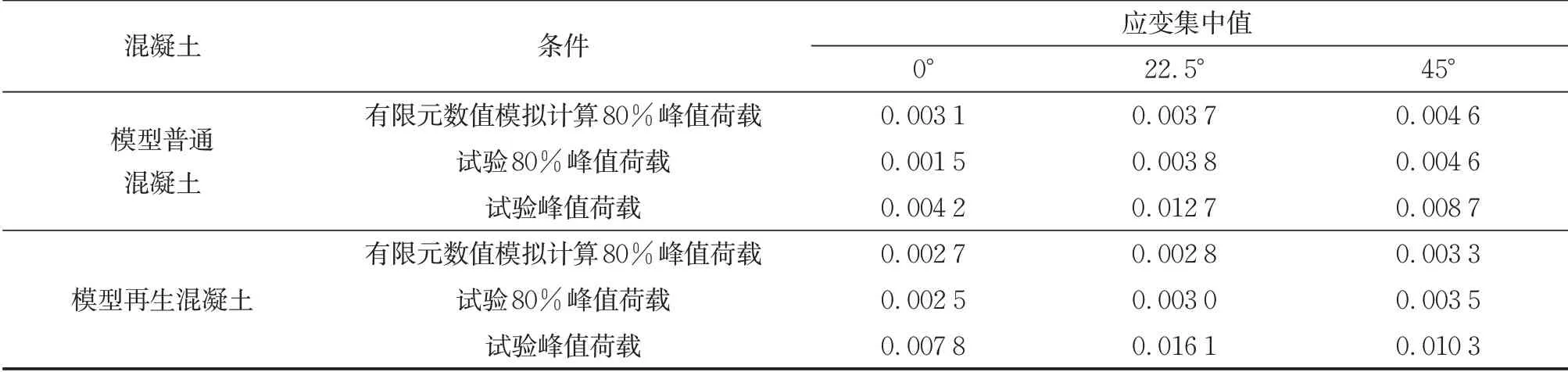
表3 试验和有限元数值模拟的应变集中值Tab. 3 Strain concentration of experimental test and FEM simulation

对比3 种骨料放置方位，骨料放置方位为0°时，开裂前骨料两侧界面区应变集中值最小，这可能是因为此时界面区处于轴心受拉的状态，所以开裂时的应变值较小；而骨料倾斜放置时，骨料尖端处硬化砂浆出现明显应变集中，但是该应变集中范围比较小，该应变集中区域受周围砂浆的保护，其应变值可以孕育到更大的值才出现开裂。综合对比分析发现，骨料放置方向为22. 5°似乎更有优势，应变集中情况能发育到更大的程度才发生开裂，而且，根据表2中几种模型混凝土的强度，可以发现骨料放置方向为22. 5°时其强度最高。

3 结论

（1）模型混凝土是将混凝土平面化，“打开黑箱”，实现了清晰观察裂缝开展过程的目的，也利用数字图像相关技术和有限元模拟，分析计算模型普通混凝土和模型再生混凝土试件的应变集中情况，得到了应变集中和裂缝发展基本规律。

（2）当模型骨料水平方向放置，即正方形骨料两侧边与加载方向平行，则应变集中首先出现在骨料两侧的界面区，应变集中发展到一定程度时发生开裂。当模型骨料放置方位为22. 5°时，应变集中首先在骨料上下两顶点孕育并向骨料两侧界面区发展成裂缝，试件强度和割线模量均高于其他两种骨料方位的情况。当模型骨料放置方位为45°时，骨料上下两顶点处出现明显的应变集中，应变集中程度也最高，该种情况的试件强度最低。

（3）在荷载达到80%峰值荷载之前，对于3种模型骨料放置方向，模型再生混凝土的应变集中程度相对模型普通混凝土的分别减轻15%、32% 和39%，是因为老砂浆的弹性模量介于天然骨料和新砂浆之间，所以应变集中能发育到更高的程度方出现开裂。

（4）根据模型骨料方位对混凝土和再生混凝土弹性模量、强度以及破坏过程的影响，不难发现，骨料尖端容易造成附近砂浆相明显的应变集中。而且，骨料不宜有较大的平整的表面，容易造成劈裂破坏的发生。因此，可采用去除骨料尖端和减少针片状骨料含量的方法对骨料和再生骨料进行优化改性。

（5）基于模型再生混凝土的研究，虽然能明晰地展示其损伤演化过程，但是该研究方法也受试验设计的局限，所以仍需更广泛地开展基于不同新老砂浆强度、不同骨料形状、不同骨料数量等参数变化的研究，才能更好地把握再生混凝土损伤演化规律。