国产703高强铝合金轴压角铝构件试验
2020-12-04胡晓光程永锋周津地郭小农韩军科邢海军
胡晓光,程永锋,周津地,郭小农,韩军科,邢海军
(1. 中国电力科学研究院有限公司,北京100055;2. 同济大学土木工程学院,上海200092)
铝合金是一种新型建筑材料,和传统的钢材相比,具有重量轻、强度高、可模性好、延展性好、耐腐蚀性好等优点。铝合金结构在建筑结构工程中的应用十分广泛,如在人行桥、门式刚架[1]、空间网格结构中均有应用。
由于铝合金弹性模量小,其受压稳定问题尤为突出,故而国内外已有很多学者致力于铝合金轴压构件的研究。早在2000年,沈祖炎等[2-3]结合上海植物园展览温室屋顶铝合金网架工程,对铝合金压杆进行了研究,得出了对称截面铝合金挤压型材压杆的稳定系数。接下来方管、圆管等闭口截面形式的铝合金轴压构件成为研究热点。朱继华等[4-6]对圆形和矩形空心截面的6061‐T5 和6063‐T6 铝合金管进行了系统研究,分析了铝合金轴压构件的稳定性能以及焊接对承载能力的影响。Maljaars 等[7]对薄壁方形构件在高温作用下的受压屈曲性能进行了试验,并测定了其几何缺陷与残余应力,得到了可以用于分析与建模的精确数据。郭小农等[8]进行了63根国产6061‐T6 铝合金挤压型材的轴压试验,并收集了142 个同类构件的试验数据,研究了构件的整体弯曲屈曲和弯扭屈曲承载力;根据材料类型的不同,提出了2 条柱子曲线,用于计算铝合金轴压构件的整体稳定承载力。
根据《铝合金结构设计规范:GB 50429—2007》[9]的规定,我国建筑结构用铝合金牌号宜采用5系和6系的普通铝合金,其中6061‐T6铝合金是目前我国最常用的结构用铝。而随着对铝合金材料研究的逐步深入,以及高精尖工程要求的逐步增高,越来越多的高性能铝合金得到了发展和应用。高强铝合金是20 世纪60 年代以航空航天用材为背景研制并发展起来的一类高性能铝合金材料。若以高强钢的比强度为标准,可将屈服强度500 MPa 以上的铝合金称为高强铝合金[10]。国外对高强铝合金材料研究起步较早,1944 年美国以诺克合金的最后方案为基础研制了75S合金,即7075合金的原型,并得到了广泛应用[11],随后在此基础上,全世界开发了数十种不同成分标准牌号的7系铝合金产品。国内对高强铝合金的研发起步较晚,20 世纪80 年代初,东北轻合金加工厂和北京航空材料研究所开始研制主要添加合金元素为锌与镁的7系铝合金。至今,我国的7系铝合金已进入实际应用阶段[12],国产703 铝合金材料是一种新研发的7系铝合金,同属Al‐Zn‐Mg‐Cu系超硬铝合金,力学性能优异,同时具有良好的耐磨性和焊接性,在航空航天和大型建筑工程中有广泛的应用前景。
目前,国内用于通信和电力的高耸塔架大多采用钢结构,随着科技水平的不断提高,人们一方面希望塔架能向着轻盈、美观的方向发展,另一方面在腐蚀性强的海洋地区或重污染区塔架又能尽量减少维护,在这些方面铝合金材料有着不可比拟的优势[13]。国产703 铝合金作为一种高强铝合金,相对于传统的6061‐T6 铝合金,其强度更高、延性更好,在塔架中有着广阔应用前景;然而当前对于703 铝合金的材料性能及其轴压构件承载性能的研究还很少。本文旨在对国产703铝合金的力学性能和轴压构件承载性能进行试验研究,得出计算轴压角铝构件极限承载力的方法。
1 国产703高强铝合金的材料性能
1.1 拉伸试验
试验目的为通过拉伸试验,得到国产703 铝合金的常温力学性能。具体力学性能指标包括抗拉强度fu、名义屈服强度f0.2、断后延伸率δ10和断面收缩率ψ。根据《金属材料室温拉伸试验方法:GB/T 228—2010》[14],在角铝构件上沿纵向取样得到拉伸试样9件。试样加工图如图1 所示。取样信息如表1所示。
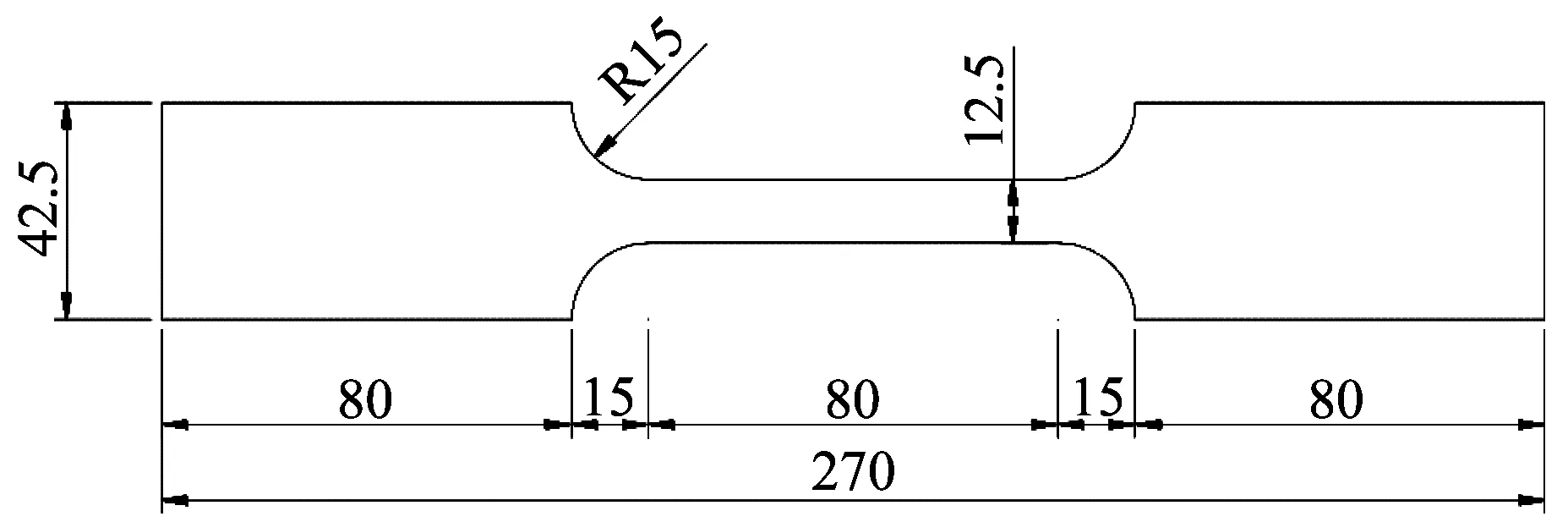
图1 标准拉伸试样加工图(单位:mm)Fig. 1 Processing drawing of standard tensile sample(unit:mm)
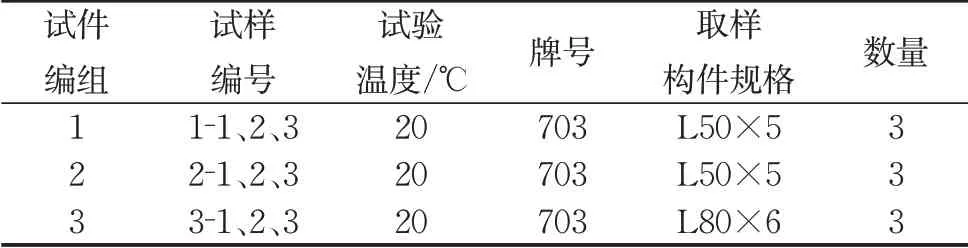
表1 取样信息汇总Tab. 1 Summary of information of sample section
由于拉伸试样在制作时可能存在尺寸误差,因此在正式试验前对所有拉伸试样的实际尺寸均进行了实测。
所有试验均在万能试验机上进行。试验中采用量程为100 mm 的位移引伸计测量应变。试验时单调加载直到试件断裂,数据采集系统可自动记录荷载、位移数据。根据《金属材料室温拉伸试验方法:GB/T 228—2010》的要求,电子试验机采用位移速率控制,位移加载速率为2. 1 mm·min−1,相对误差为±20%。
部分拉断后的拉伸试样如图2所示。部分试件的应力‐应变曲线如图3。每个试样的力学性能详见表2,表中给出的具体力学性能指标包括弹性模量E,抗拉强度fu、名义屈服强度f0.2、断后延伸率δ10和断面收缩率ψ。其中,1‐1 的材料强度和3‐3 的弹性模量与整体数据差距过大,视作异常数据。
根据表2,剔除无效数据后,测得国产703 高强铝合金的弹性模量平均值E=73 305. 75 MPa,名义屈服强度f0.2= 490. 8 MPa,极限强度fu= 520. 6 MPa。
1.2 本构关系
前人对铝合金的本构关系已经作了相当多的研究,其中最常用的是Ramberg‐Osgood(R‐O)模型。Ramberg 和Osgood 于1939 年提出了采用3 个参数描述铝合金本构关系的模型[15]。该模型的表达形式如下:


图2 拉断后的拉伸试样Fig. 2 Tensile specimen after breaking
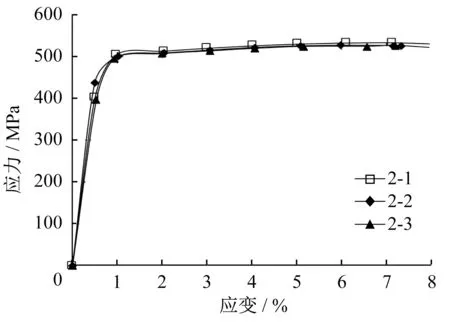
图3 部分拉伸试件的应力⁃应变曲线Fig. 3 Stress-strain curves of some tensile specimens
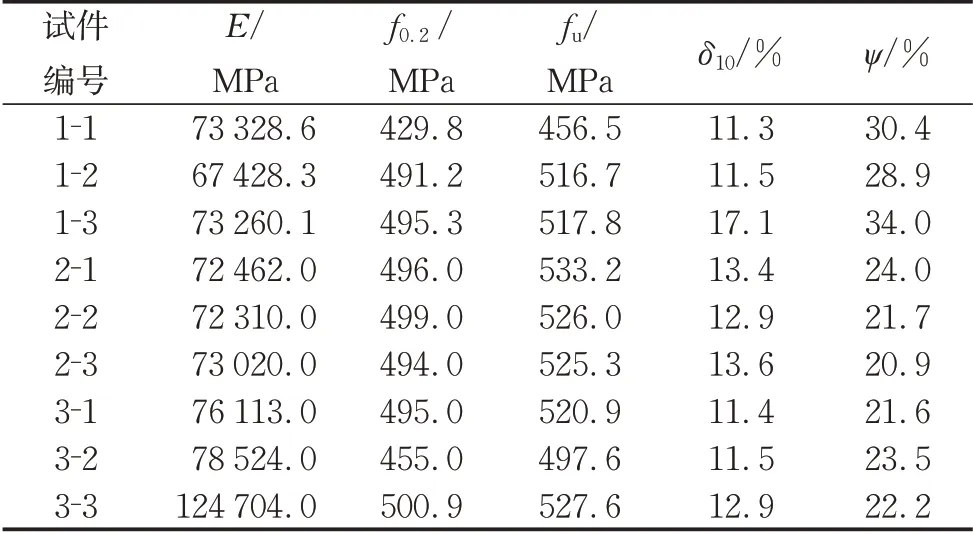
表2 拉伸试样的力学性能指标Tab. 2 Mechanical properties of tensile specimens
式中:E为原点处的弹性模量;n和B为由试验测定的参数。设f0.2为残余应变等于0. 002时所对应的应力,则由式(1)可得
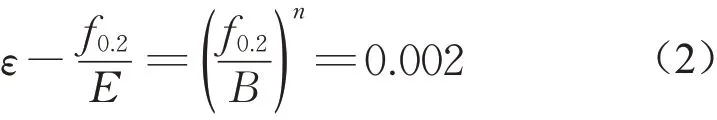
把式(2)代入式(1)可得

由式(3)可知,n是描述应变硬化的参数。n=1时,材料的应力应变关系是线弹性的;n=∞时,材料的应力应变关系是理想弹塑性的。指数n对应力应变曲线的影响很大,而规范中一般并不会给出指数n的数值,Steinhardt 通过研究,于1971 年提出了n的近似计算公式[16]

式中:f0.2单位为MPa。
本节根据实测的应力应变曲线,拟合得到了拉伸试样的R‐O 拟合曲线,其中硬化指数n的取值采用Steinhardt 建议,应变区间为0~2%,选取部分试验曲线如图4所示。从图4可以看出,各试件的实测曲线和理论曲线均十分接近,而仅在曲线拐弯处略有差别,多数试件的理论曲线比实测曲线先拐弯。因此,国产703 高强铝合金的本构关系满足R‐O 模型和Steinhardt建议。

图4 部分实测应力应变曲线和R⁃O理论曲线的对比Fig. 4 Comparison of measured stress-strain curve of test piece with R-O theoretical curve
2 国产703高强铝合金轴压角铝试验
2.1 试验概况
为探究国产703高强铝合金角铝的轴压承载性能,共设计了24 根构件,构件截面尺寸取为工程中常见规格,分别为L50×5 和L80×6;为了研究长细比对轴压构件承载力的影响,每种截面设置了4 种长细比;为减少试验偶然误差,每组设置3个相同构件。由于构件在制作时可能存在尺寸误差,因此在正式试验前对所有轴压构件的实际尺寸进行了实测,构件截面详图如图5所示,构件信息汇总见表3。实测计算长度为两端转动中心的间距,是在测得实测长度后考虑刀口板厚度的影响后得到的,即实测长度加上两侧刀口板净厚度,为实测计算长度;其中刀口板静厚度为刀口板厚度减去槽口深度。根据实测计算长度和实测截面,可计算出实测长细比。

图5 截面尺寸(单位:mm)Fig. 5 Section size(unit:mm)
2.2 构件初始缺陷的测量
金属构件的屈曲性能通常会受到初始几何缺陷的影响,因此对试验构件进行仔细的几何缺陷测量是角铝轴压试验必不可少的重要环节。
本试验采用LVDT(linear variable differential transformer)直线位移传感器测量构件的初始缺陷。在L型构件外侧表面共选取6条线,每条线上选取7个等间距点的位置进行测量。具体的测量位置如图6 所示。图7 展示了典型的L50‐703‐40A 构件的初始缺陷测量情况。

图6 构件初始缺陷测量线的横截面位置Fig. 6 Cross-section position of initial defect measurement line of component
2.3 试验装置和方法
本试验采用千斤顶单调加载。为了准确模拟双向铰支座,构件两端设置了双向刀口,如图8 所示。双刀口支座由3 块钢板组成,它在两个方向都有很好的转动能力。端板上预先开好了与试件截面形状相同的槽口,安装时将试件卡入槽口。
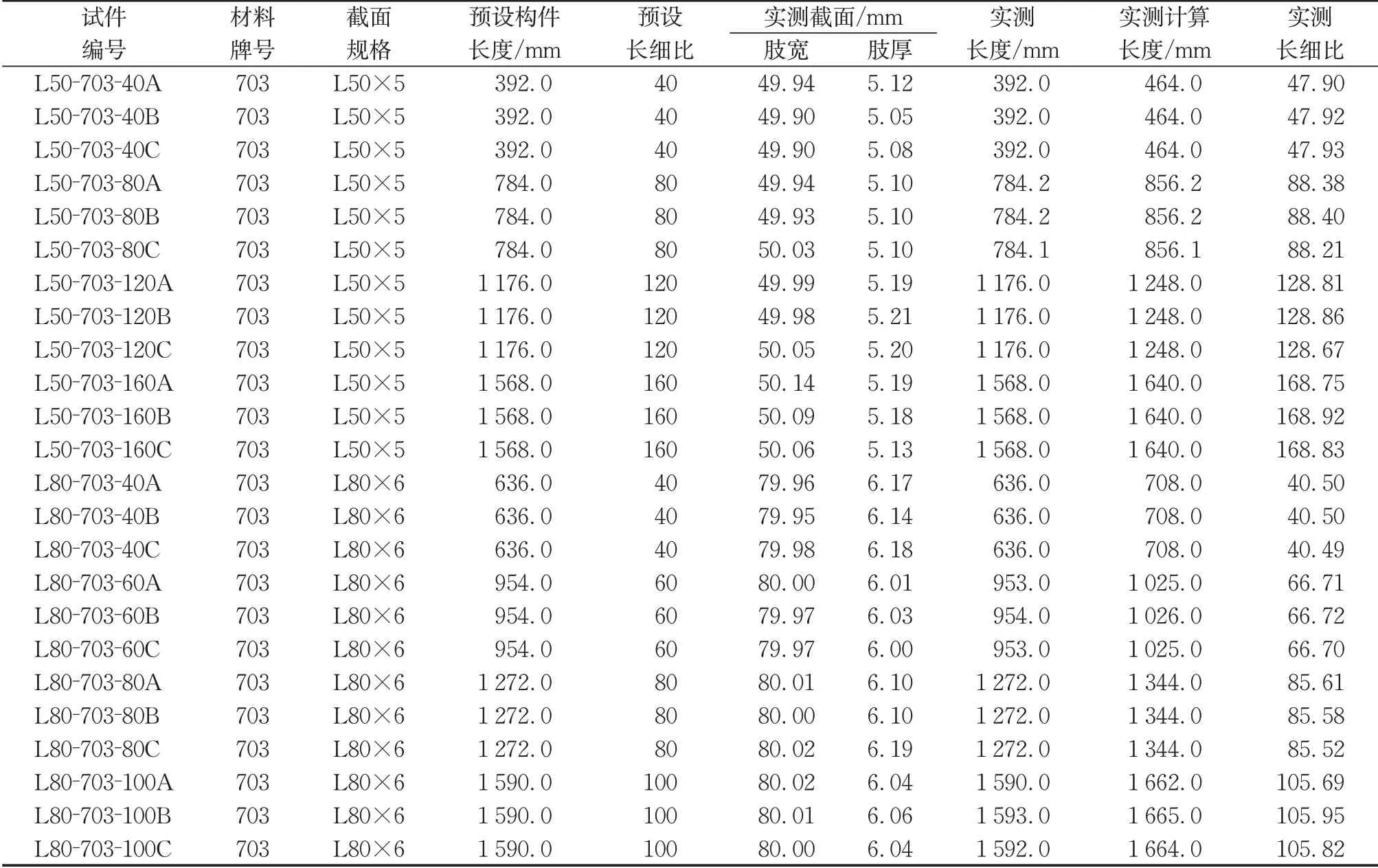
表3 构件信息汇总Tab. 3 Summary of component information
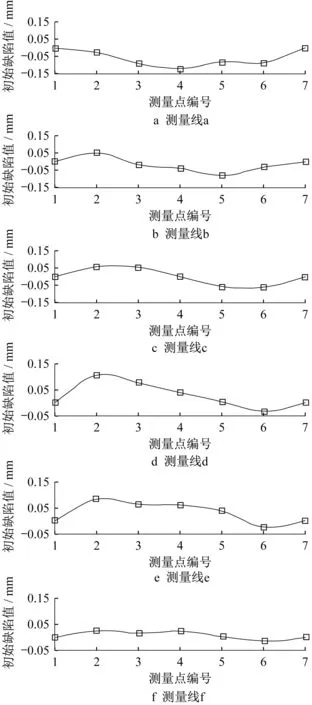
图7 部分典型的构件初始缺陷测量结果Fig. 7 Measurement results of typical initial defects of some members
试验时将试件两端置于双刀口支座中,为了测得跨中截面处的纵向应变和水平位移,在构件跨中截面布置了一定数量的应变片和位移计。图9给出了构件跨中截面上应变片及水平位移计的布置情况,位移计D1沿截面x向平行布置,D2、D3沿截面y向平行布置。

图9 跨中截面的位移计和应变片布置图Fig. 9 Layout of displacement gauge and strain gauge across mid-section
本试验中所有构件均采用竖向放置。构件在双刀口支座中几何对中后,先施加较小荷载,然后调整构件位置,使构件跨中截面上各应变片的读数基本一致,则此时已精准对中,然后卸载。
所有构件均采用单调分级加载。以每级0. 1Pu(理论承载力)分步施加荷载,每个荷载步施加完成后稳定2~3 min,应变和位移均采用计算机数据采集系统自动采集,待数据采集完成后继续施加下一级荷载。当构件接近极限承载力时,采用缓慢连续加载,构件达到极限承载力之后继续施加荷载,直到构件出现明显的变形,然后开始缓慢卸载直至荷载为零。
2.4 试验结果与分析
对整个试验过程的观测表明,试件在试验过程中能得到较好的控制,703型铝合金轴压构件具有较好的延性和后期承载能力。本试验共计完成国产703 高强轴压角铝构件共24 件,所有试件的极限承载力和破坏模式汇总于表4。
当构件的长细比较小时,构件发生弯扭失稳;而当构件长细比较大时,构件发生弯曲失稳。在受荷初期,构件的变形和形态变化均不大。对于长细比大的构件,当外荷载增加至极限荷载的80%~90%时,构件开始出现较为明显的整体弯曲;随着外荷载的继续增加,构件弯曲幅度和跨中截面的平面内位移逐渐增大;随后,构件进入破坏阶段,整体弯曲非常明显,直至从两侧刀口支座脱落。对于长细比小的构件,在未破坏前仅能观察到轻微的变形,当加载达到极限荷载后,构件突然于跨中截面处扭转破坏。
图10绘制了部分试件的荷载‐应变曲线,其中横轴均为跨中截面测点处的应变。对于长细比较小的试件,加载初期荷载‐应变曲线呈线性变化,当荷载到达极限承载力的80%左右时,跨中截面一侧的压应变迅速增大,另一侧的压应变增长速率逐渐减小,直至开始负增长。当荷载达到峰值时,构件瞬间出现弯扭失稳破坏。
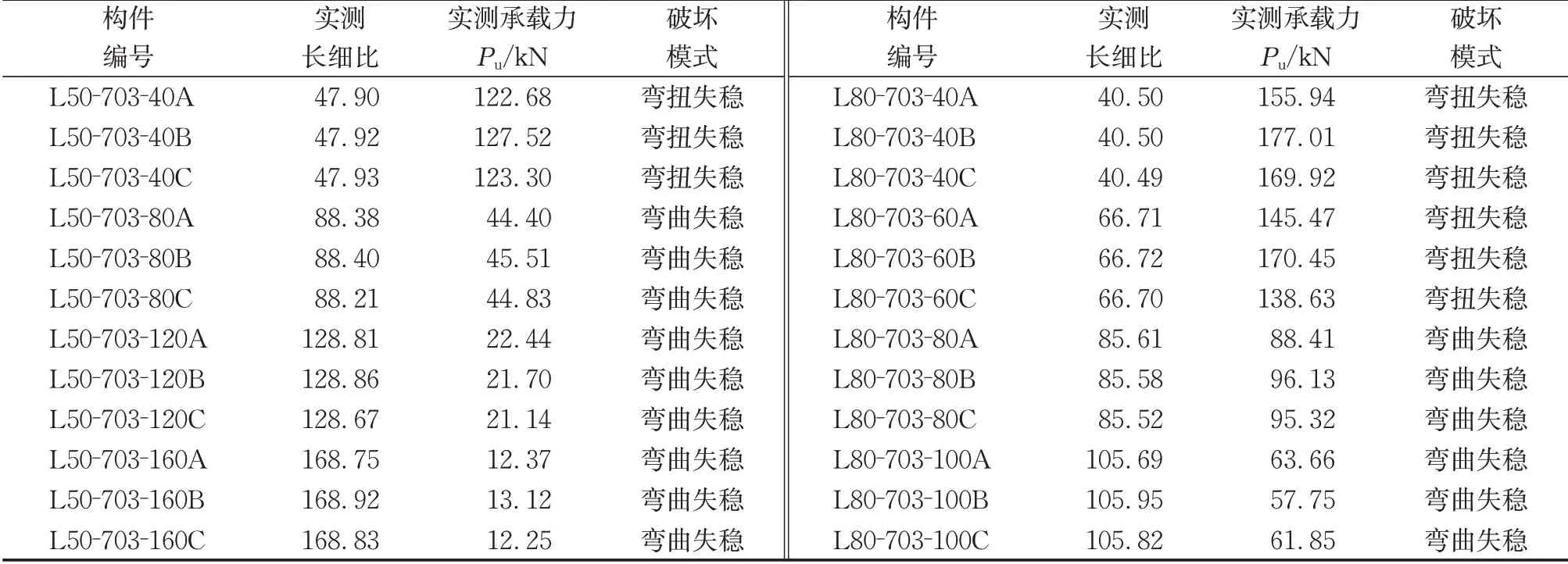
表4 轴压构件的实测极限承载力汇总Tab. 4 Summary of measured ultimate bearing capacity of axial compression members
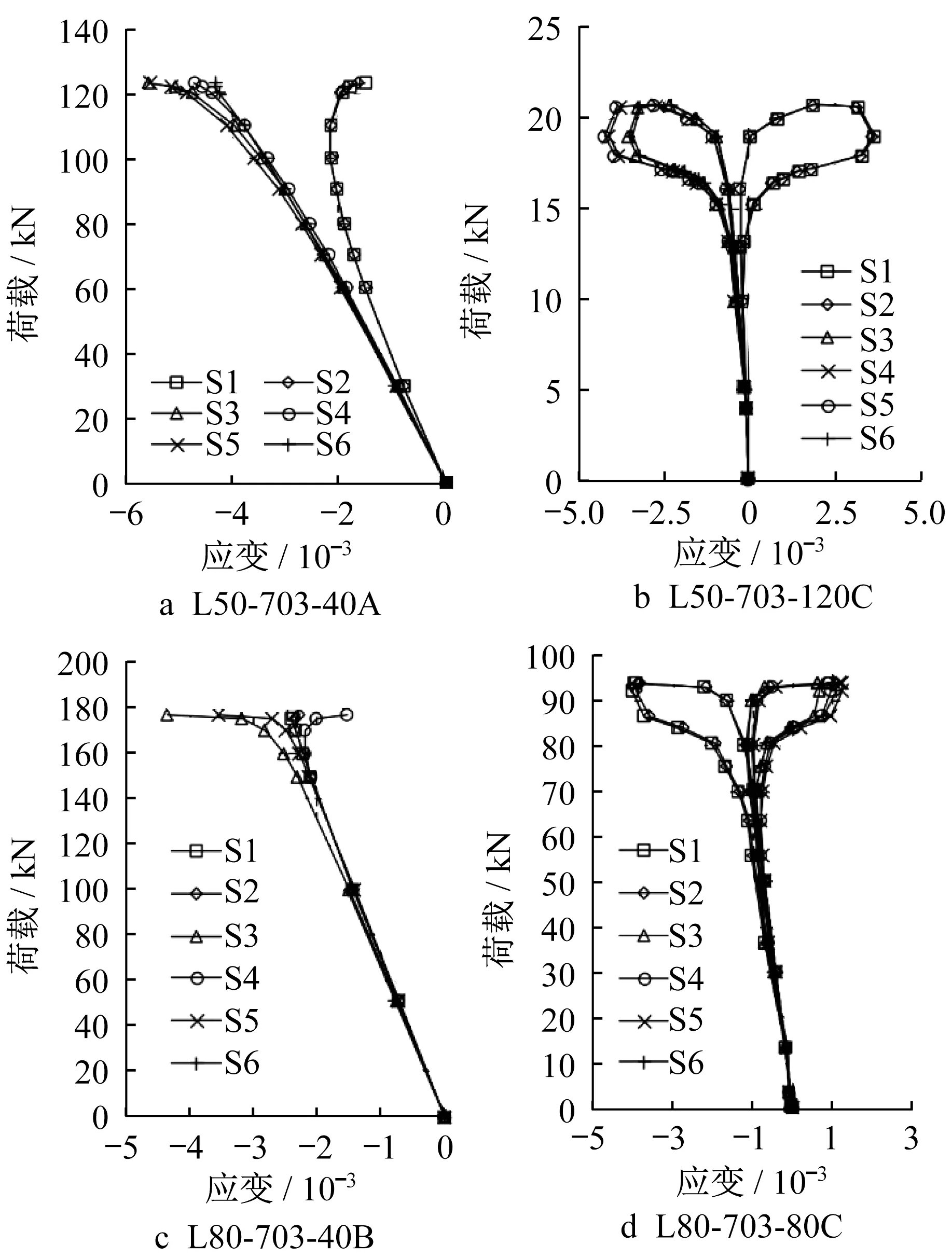
图10 典型荷载⁃应变曲线Fig. 10 Typical load-strain curve
对于长细比较大的试件,加载初期荷载-应变曲线也呈线性变化,当荷载到达极限承载力的80%左右时,跨中截面受压侧的压应变增长的速率逐渐增加,而另一侧的压应变逐渐负增长,构件发生明显弯曲,直至峰值荷载。与弯扭失稳不同的是,弯曲失稳的试件在达到峰值荷载前受拉侧已有明显拉应变。峰值荷载出现后,随着加载的继续进行,应变会显著增加,而荷载则缓慢减小。
图11 给出了部分试件的跨中截面典型的荷载‐位移曲线,其中横轴均为跨中截面各测点处位移计所测得的位移。对于长细比较小的试件,加载初期荷载‐平面内位移呈线性变化,平面外位移几乎没有变化。当荷载达到极限承载力的80%左右时,构件平面内位移迅速增大,且平面外位移也有了较明显的增加。当荷载达到峰值时,突然出现弯扭失稳破坏,弯扭失稳时构件的变形主要是扭转变形以及绕非对称轴的弯曲。

图11 典型荷载⁃位移曲线Fig. 11 Typical load-displacement curve
对于长细比较大的试件,加载初期荷载‐位移也呈线性变化,当荷载达到极限承载力的80% 左右时,构件平面内位移迅速增大,且平面外位移仍几乎没有变化。与弯扭失稳不同的是,弯曲失稳的试件在达到峰值荷载后,平面内位移始终保持在较低的水平。
3 数值分析
3.1 数值分析模型
本文采用ANSYS 软件对国产703 轴压角铝构件的极限承载力和破坏模式进行了数值计算。703轴压角铝构件模型采用BEAM188 单元建模,构件沿纵向划分为20 段。铝合金材料的本构关系采用Ramberg‐Osgood 模型[15]和Steinhardt 建议来描述,力学性能指标根据本文第1. 1节拉伸试验平均值取值。有限元模型的边界条件与试验设置的边界条件相同。计算中同时考虑材料非线性和几何非线性的影响。构件的初始弯曲根据实测结果取值。
3.2 数值分析结果
对于长细比较小的弯扭失稳构件,数值模型的破坏模式与实际破坏情况对比如图12所示,数值模型预测的破坏模式为弯扭失稳,与试验结果相同。图13 绘制了试件L80‐703‐60C 的实测荷载‐位移曲线和数值模型预测的荷载‐位移曲线。从图13 中可以看出,实测值和数值计算结果吻合较好。
表5列出了弯扭失稳轴压构件的数值分析承载力PFE和实测承载力Pu的比较。结果表明,数值分析结果与试验结果吻合良好,平均偏差为6. 06%。因此,数值分析模型可以准确模拟弯扭失稳铝合金轴压构件的极限承载力和破坏模式。
对于长细比较大的弯曲失稳构件,数值模型的破坏模式与实际破坏情况的对比如图14所示,数值分析模型预测的破坏模式为弯曲失稳,与试验结果相同。图15绘制了试件L50‐703‐120C的实测荷载‐位移曲线和数值模型预测的荷载‐位移曲线。从图中可以看出,实测值和理论值吻合较好。
表6 列出了弯曲失稳构件的数值分析承载力PFE和实测承载力Pu的比较。结果表明,数值分析模拟结果与试验结果吻合良好,平均偏差为2. 12%。

图12 有限元与试验弯扭失稳形状对比Fig. 12 Comparison of shapes of FEM and buckling torsional member

图13 弯扭失稳构件荷载⁃位移曲线的比较Fig. 13 Comparison of load-displacement curves of bending and torsional members and FEM
综上所述,数值分析模型可以准确模拟弯扭失稳的国产703高强轴压角铝构件的极限承载力和破坏模式。
由前文中的试验对比结果可知,数值分析模型可以准确模拟703铝合金轴压构件的极限承载力和破坏模式。为了进一步分析国产703高强轴压角铝构件的屈曲性能,本文建立了大量的数值分析模型,并利用该数值模型针对长细比、截面规格等因素对构件承载力的影响规律进行了全面的分析。
数值模型的部分参数取值如下:铝合金挤压成型过程中的残余应力很小,可以忽略不计[17]。根据《铝合金建筑型材:GB/T 5237—2017》[18]的规定,高精级铝合金构件的初弯曲不得超过0. 000 8L(L为铝合金构件长度)。因此,在数值分析中,可偏安全地将初始几何缺陷设置为L/1 000。同时,国产703铝合金的屈服强度和弹性模量根据本文第1. 1节的拉伸试验结果取值。
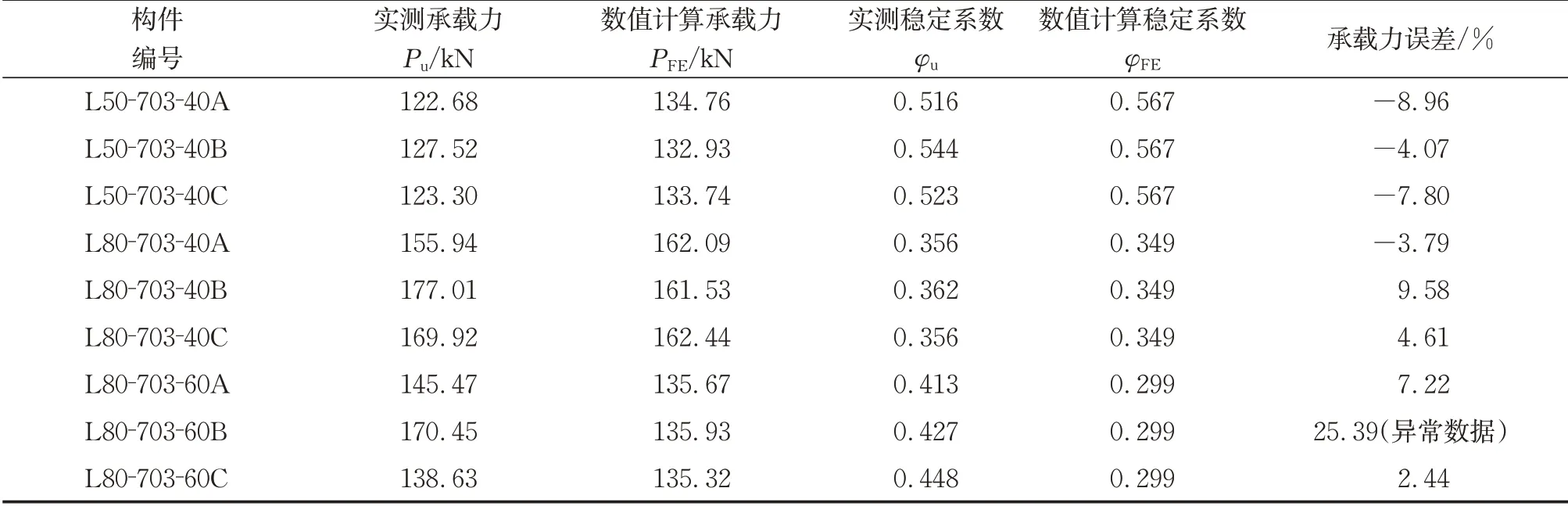
表5 弯扭失稳构件极限承载力比较Tab. 5 Comparison of ultimate bearing capacity of bending and torsional instability members
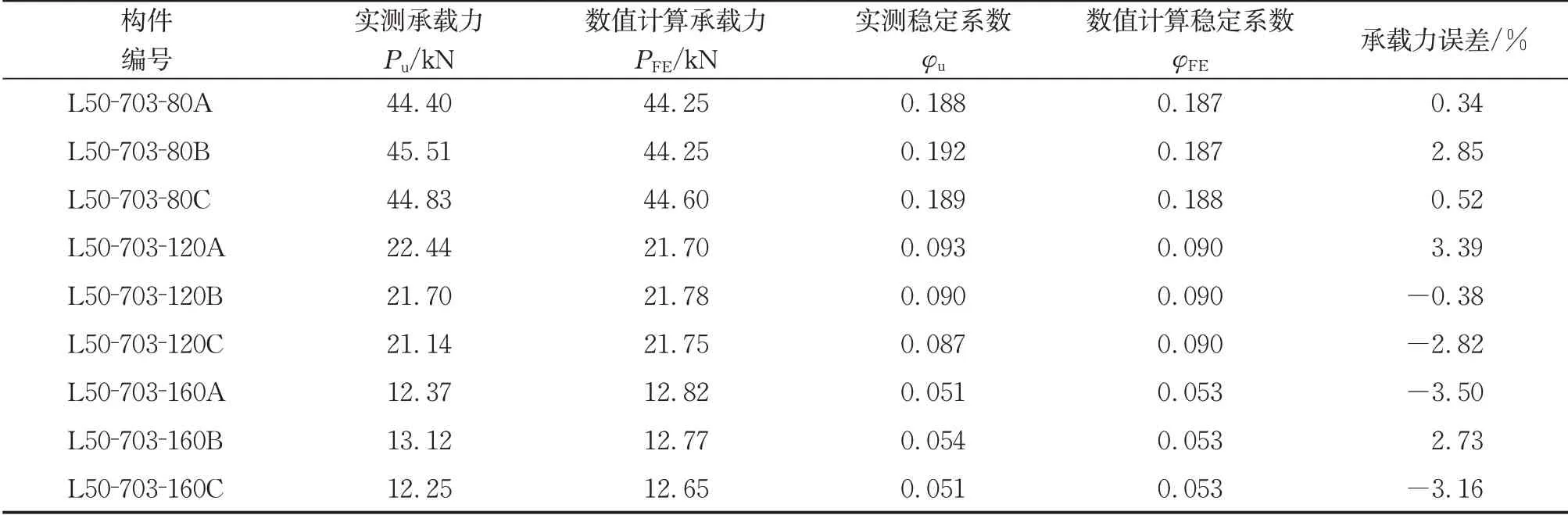
表6 弯曲失稳构件极限承载力比较Tab. 6 Comparison of ultimate bearing capacity of bending instability members

图14 有限元与试验弯曲失稳形状对比Fig. 14 Comparison of shapes of FEM and bending member
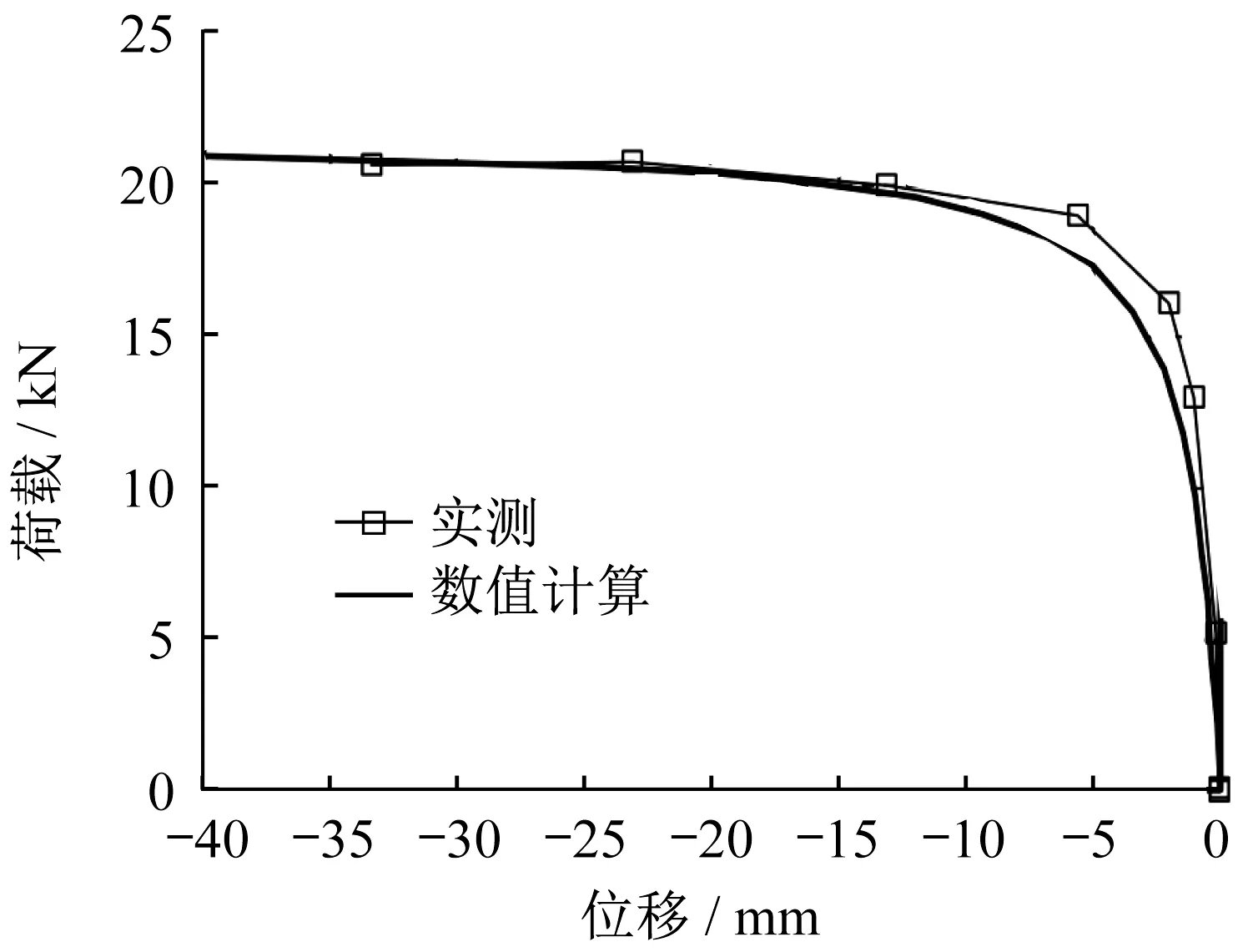
图15 弯曲失稳构件荷载⁃位移曲线的比较Fig. 15 Comparison of load-displacement curves of bending members and FEM
在此基础上建立数值模型。共考虑了5种截面规格,取工程中常见的5 种规格,分别为L50×5、L80×6、L100×8、L125×12 和L160×14。每种截面考虑120个长细比。同时考虑材料非线性和几何非线性的影响,共得到600个数值计算结果,并将计算结果统计整理,绘制稳定系数‐相对长细比曲线,并与欧拉曲线、规范曲线相对比,结果如图16所示。
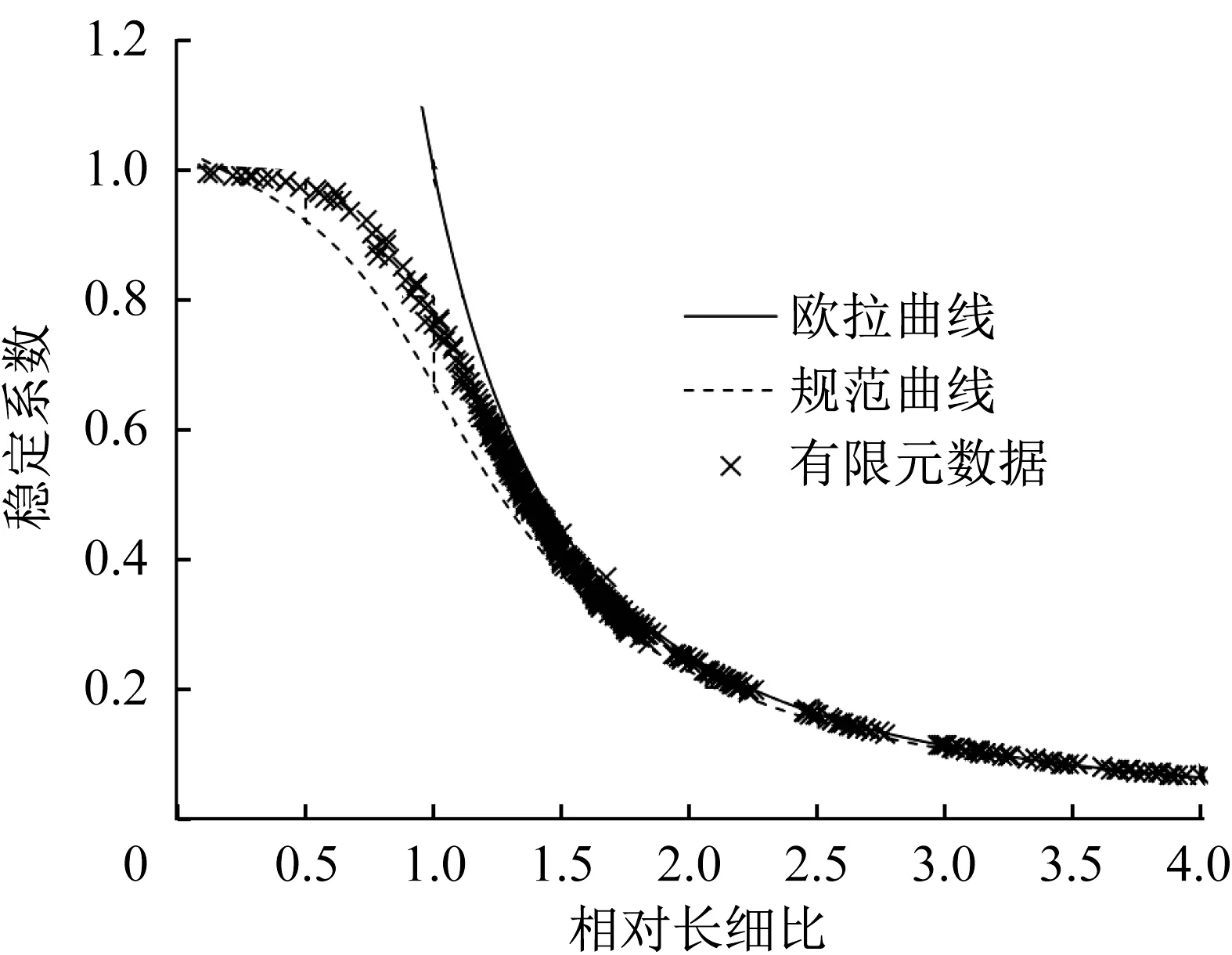
图16 数值分析结果与欧拉曲线和规范曲线对比Fig. 16 Comparison of numerical analysis results with Euler and code curves
4 理论研究与对比
4.1 我国规范计算方法
根据我国《铝合金结构设计规范:GB 50429—2007》[9],对于非焊接单轴对称截面轴心受压构件的整体稳定承载力可以采用以下公式计算:

式(5)~(7)中:Nuk为轴压构件的整体稳定承载力标准值;ηe为考虑板件局部屈曲的修正系数,当受压板件的全截面有效时,可取ηe=1;ηas为截面非对称性系数;A为构件的毛截面面积;f0.2为材料名义屈服强度标准值;φ为整体稳定系数;-λ是柱的相对长细比,为构件考虑初始弯曲及初偏心的缺陷系数,703 属于弱硬化合金,可取α=0. 2,-λ0=0. 15。当构件发生绕对称轴的弯扭失稳时,计算稳定系数时应采用等效弯扭长细比λyω代替λy,弯扭等效长细比的计算公式可参考《铝合金结构设计规范:GB 50429—2007》,本文不再赘述。
4.2 试验结果和数值分析结果与规范曲线比较
我国《铝合金结构设计规范:GB 50429—2007》中的φ‐-λ曲线计算出的是稳定系数的标准值[8],则可以将数值分析结果与规范进行对比,如图16 所示。结果表明,数值分析结果和我国《铝合金结构设计规范:GB 50429—2007》中的弱硬化铝合金柱子曲线吻合较好。数值分析结果和规范公式的φ值之比的平均值为1. 094,标准差为0. 043,变异系数为0. 040。
同理,图17给出了我国规范φ‐-λ曲线和实测数据点的对比。结果表明,试验数据和我国《铝合金结构设计规范:GB 50429—2007》中的弱硬化铝合金柱子曲线吻合也较好。试验数据和规范公式的φ值之比的平均值为1. 072,标准差为0. 053,变异系数为0. 052。综合以上两则结果,说明规范公式能有效、准确地计算国产703 高强轴压角铝构件的极限承载力。
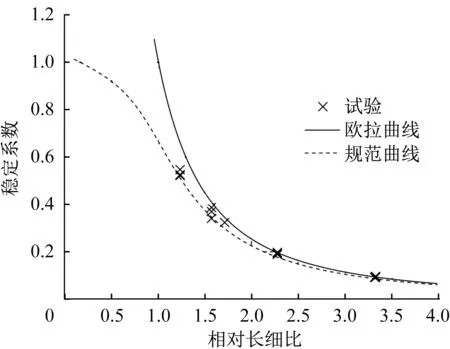
图17 试验结果与欧拉曲线和规范曲线对比Fig. 17 Comparison of test results with Euler and code curves
5 结论
(1)本文完成了国产703 高强铝合金的拉伸试样试验,获得了其物理力学性能和本构关系,结果显示,703 高强铝合金的强度和延性都较为优异,其本构关系可以用Ramberg‐Osgood模型和Steinhardt建议来描述。
(2)完成了24 根国产703 高强轴压角铝构件承载力试验,得到了该类构件在轴压作用下的极限承载力和破坏模式。结果表明,703高强角铝构件的长细比较小时发生弯扭失稳,长细比较大时发生弯曲失稳。
(3)采用ANSYS 软件建立了数值模型,与试验数据相对比后发现,数字化模型能准确模拟国产703高强轴压角铝构件的破坏模式,数值计算得出的极限承载力以及破坏模式和试验结果十分接近。
(4)完成了大量数值计算,试验结果和数值分析结果均表明,我国《铝合金结构设计规范:GB 50429—2007》的弱硬化铝合金柱子曲线可用于计算国产703高强轴压角铝构件的整体稳定系数。
