一道中考压轴题的解析及拓展
2020-12-03姜树峰江苏省南通市通州区平潮实验初中226361
姜树峰 (江苏省南通市通州区平潮实验初中 226361)
1 题目来源
题目(2019年江苏·南通卷第28题第3问)定义:点M(x,y),若x,y满足x2=2y+t,y2=2x+t,且x≠y,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点P(m,n).若点Q(n,m)是“线点”,直线PQ分别交x轴、y轴于点A,B,当|∠POQ-∠AOB|=30°时,直接写出t的值.
对于x2=2y+t①,y2=2x+t②,联立成常见的方程组,由①-②,得(x+y)(x-y)=-2(x-y),由于x≠y,得x+y=-2.利用数形结合,将未知数赋予点的坐标,x+y=-2的图象是一条直线,点M在直线x+y=-2上,即新定义的“线点”的内涵.
如图1,OP=OQ(或OP1=OQ1),OA=OB,∠AOB=90°.将这样一个常见的图形放到坐标系中(图2),点P(或P1),Q(或Q1),A,B在直线x+y=-2上.怎么做到呢?让Q是“线点”,让点P的横坐标等于点Q的纵坐标,点P的纵坐标等于点Q的横坐标,自然点P也就是“线点”,且点P,Q关于直线y=x对称,自然OP=OQ.直线PQ分别交x轴、y轴于点A,B,就得到OA=OB,∠AOB=90°.
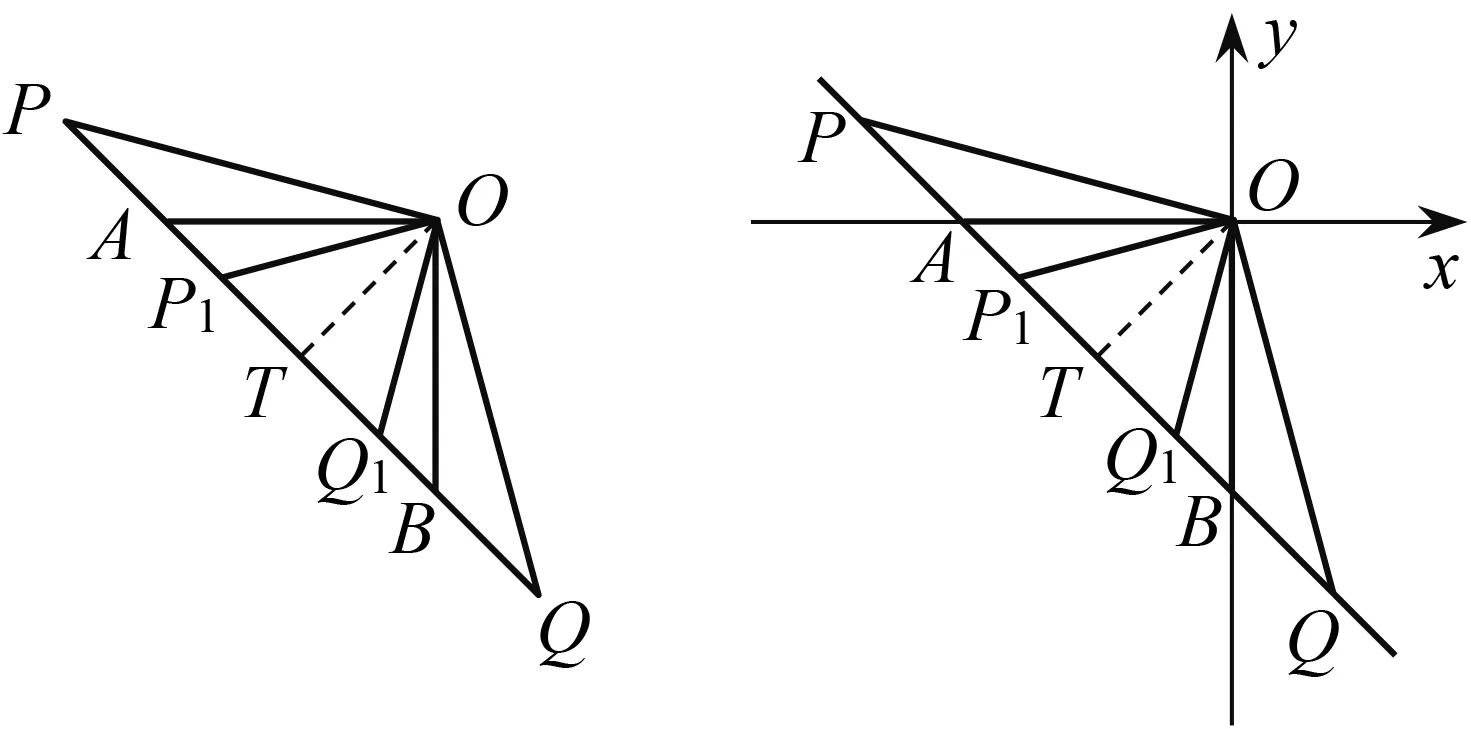
图1 图2
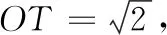
2 拓展
2.1 互换题设和结论
定义:点M(x,y),若x,y满足x2=-2y+t,y2=-2x+t,且x≠y,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点P(m,n).若点Q(n,m)是“线点”,直线PQ分别交x轴、y轴于点A,B,当t=6 时,求|∠POQ-∠AOB|.
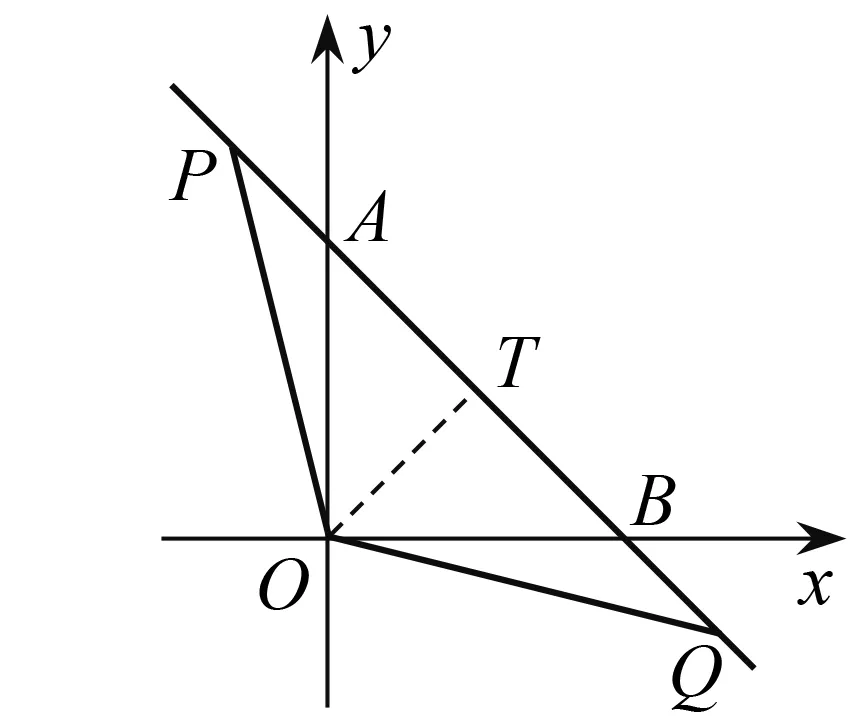
图3
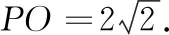
2.2 拓展一
定义:点M(x,y),若x,y满足x2=ay+t,y2=ax+t,且x≠y,a,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点P(m,n).若点Q(n,m)是“线点”,直线PQ分别交x轴、y轴于点A,B,当∣∠POQ-∠AOB∣=α时,0°<α<90°,求t的值.
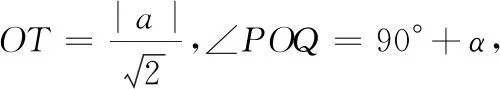
2.3 拓展二
(1)定义:点M(x,y),若x,y满足x2=2y+t,y2=2x+t,且x≠y,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点P(m,n),m<-1,n>-1.若点Q(n,m)是“线点”,T为线段PQ的中点,D为线段OT上任一点,∠POQ=α.连结DP,将线段DP绕点D逆时针旋转180°-α,点D的对应点是点E.随着点D在线段OT上位置的变化,点E的位置也在变化.求证:当α确定时,点E在一条直线上.
如图4,对于等腰三角形POQ,T为底PQ的中点,D为线段OT上任一点,∠POQ=100°.连结DP,将线段DP绕点D逆时针旋转80°,点D的对应点是点E,当点E在直线OT上时,容易发现QE∥PO.当点P,Q的位置变化,T的位置不变,点E的位置变化有什么特性呢?由此编制出这题.
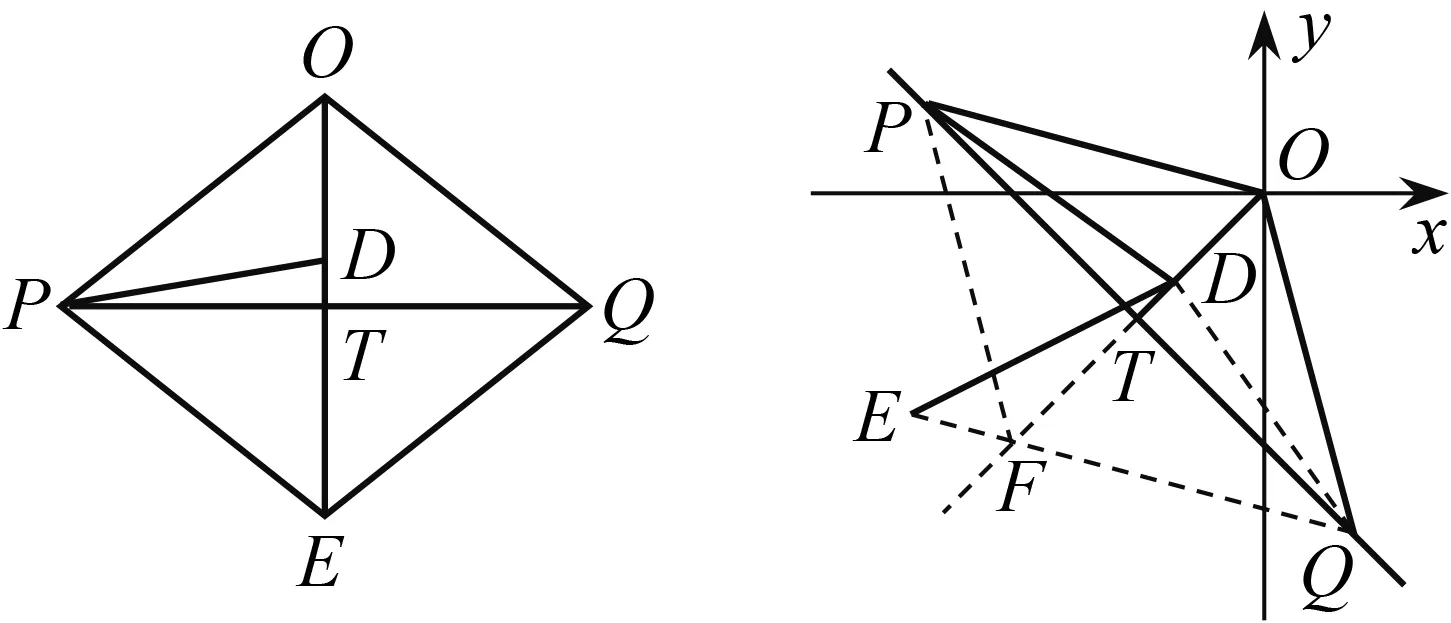
图4 图5
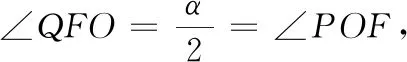
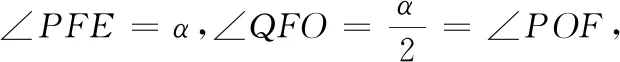
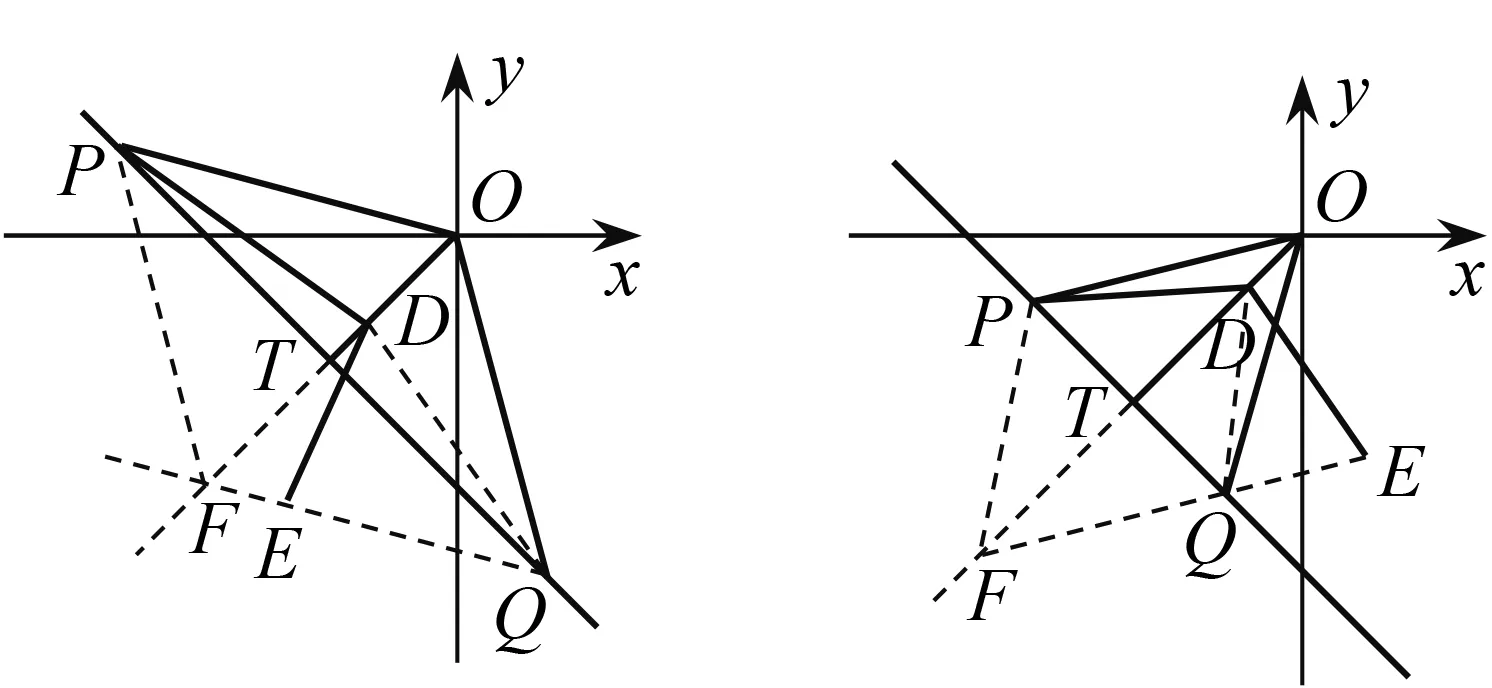
图6 图7
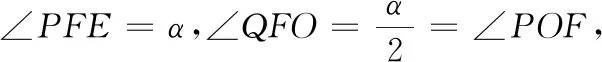
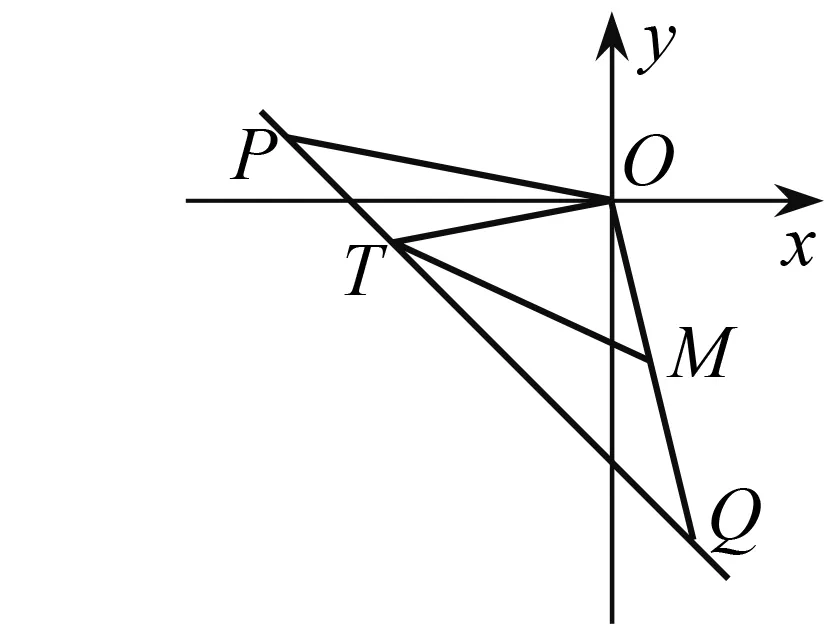
图8
(2)定义:点M(x,y),若x,y满足x2=2y+t,y2=2x+t,且x≠y,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点P(m,n),m<-1,n>-1.若点Q(n,m)是“线点”,M为线段OQ上一点,如果在线段PQ上有两个“线点”T,使∠OTM=∠OQP,求QM长的范围(用t表示).
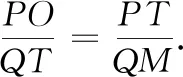
有两个“线点”T,与一元二次方程根的判别式相联系,别样的数形结合.原题定义中引进了参数t,这样的新编制让参数t的意义充分体现.
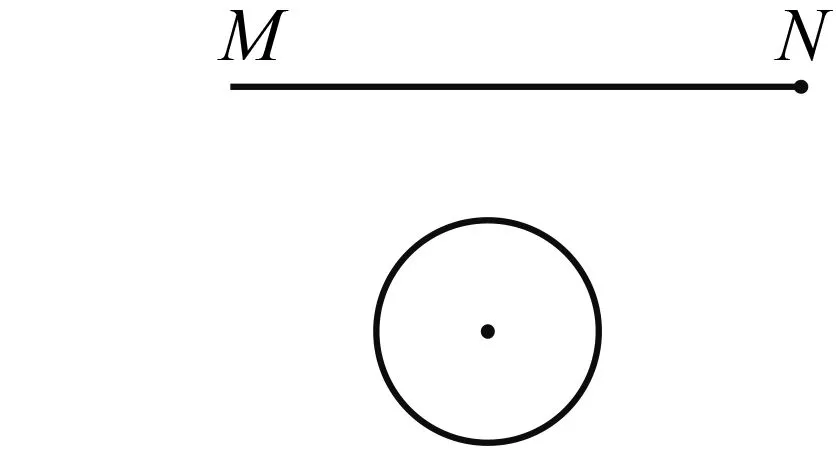
图9
(3)定义:点M(x,y),若x,y满足x2=ay+t,y2=ax+t,且x≠y,a,t为常数,则称点M为“线点”.已知:在直角坐标系xOy中,点Q(n,m)是“线点”,求|n|+|m|的最小值.
问题解决某市要修建一条通往圆形景观湖的道路,如图9,道路以N为起点,先沿NM方向到某处,再在该处拐一次直角弯到湖边,如何修建能使道路最短?
分析 (x+y)(x-y)=-a(x-y),由于x≠y,得x+y=-a,直线x+y=-a与x轴交于点A(-a,0),与y轴交于点B(0,-a).OA=OB=|a|.当点Q在线段AB上时(含点A,B),如图10,过点Q作QR⊥x轴于点R,因为∠OAB=45°,所以QR=AR,|n|+|m|=OR+QR=OA=|a|.当点Q不在线段AB上时,|n| + |m|>OA=|a|,所以|n|+|m|的最小值为|a|.
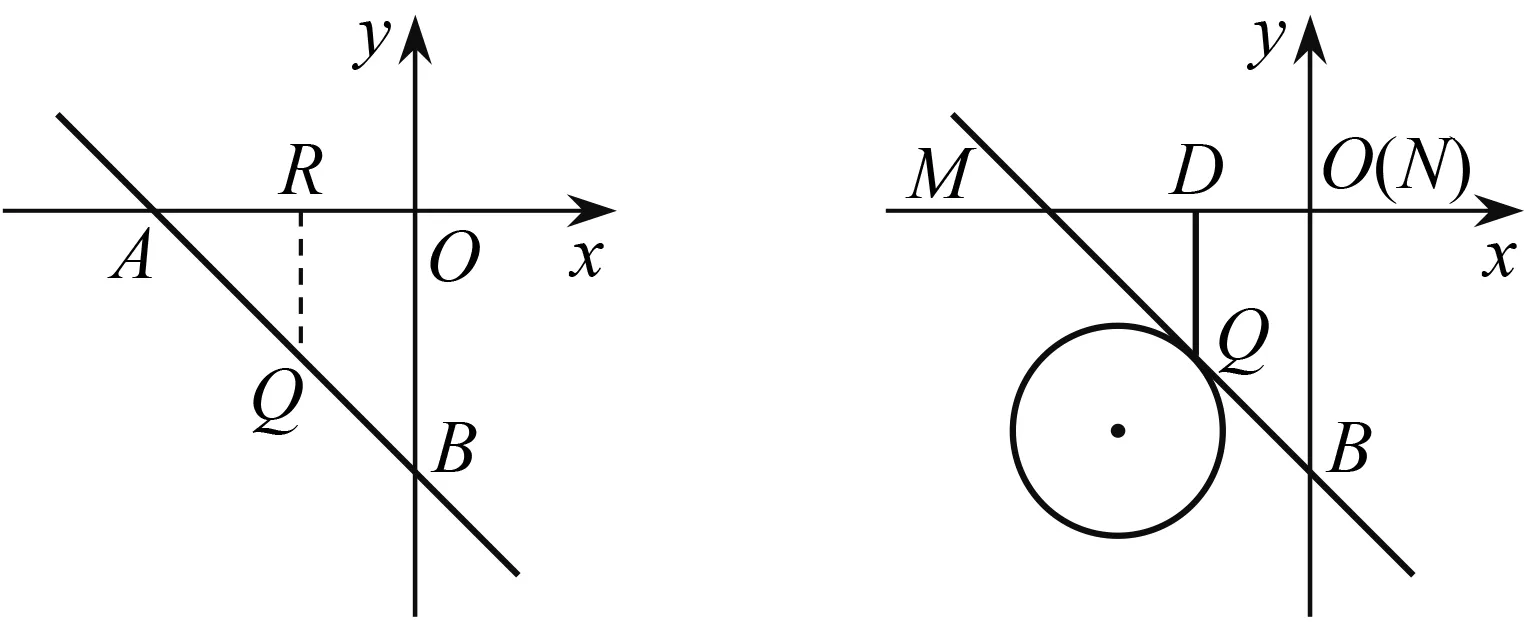
图10 图11
如图11,以N为原点、直线MN为x轴建立平面直角坐标系.沿x轴负方向平移直线x+y=0,直到直线与圆第一次相切时停止.设切点为Q,过点Q作QD⊥x轴于点D.修建方案:先沿NM方向修建到D处,再沿DQ方向修建到Q处.设点Q(n,m),由Q为“线点”,|n|+|m|的最小值为|a|,OD+DQ=|n|+|m|,OD+DQ的最小值为|a|.如果接着沿x轴负方向平移直线x+y=0, |a|会增大,OD+DQ会增大.
说明 将原题中的新定义再拓展为一般情形,探究出“线点”的特性——横坐标、纵坐标的绝对值的和的最小值为|a|.再利用“线点”的这一特性解决实际问题.实际问题与“线点”的特性结合得相当精妙.
