美英早期代数教科书中的方程定义
2020-12-03杨孝曼汪晓勤华东师范大学教师教育学院200062
杨孝曼 汪晓勤 (华东师范大学教师教育学院 200062)
1 引言
方程是代数学的基石,是用数学符号刻画现实世界的重要工具.在古代,虽然还没有形成方程的概念,但由于实践需要,人们已经会用方程解决实际问题了.“方程”这个名词最早见于汉代数学典籍《九章算术》,指的是多元线性方程组.刘徽注称:“程,课程也.群物总杂,各列有数,总言其实.令每行为率,二物者再程,三物者三程,皆如物数程之,并列为行,故谓之方程.”[1]“如物数程之”的意思是需要求几个未知数就要列几个方程.晚晴数学家李善兰和英国传教士伟烈亚力在翻译德摩根的《代数学》时,首次将equation译为“方程”.至此,方程这一中国古代数学术语被注入了新的内涵而沿用至今.
人教版和苏教版五年级数学教科书均将“方程”定义为“含有未知数的等式”,并在例题和课后习题中设有方程的判断题.该定义体现了教材重形式轻本质的特点.据了解,在实际教学过程中,一些教师甚至会用“含有字母的等式”来代替方程的定义,这种过度解读非常不利于学生对方程本质的理解.同时,“含有未知数的等式”这个定义也带来了很多引起争议的问题,例如很多教师和学生都存在这样的疑问:x=1是方程吗?x+1=x+2是方程吗?在英语里用equation表示方程,而equation原来就是等式的意思,那么前人在翻译这个单词时,为什么不直接用等式?方程与等式的联系与区别到底在哪里?
若要回答以上问题,就必须真正理解方程的本质.著名数学史家M·克莱因(M.Kline,1908—1992)曾说:“课本上斟字酌句的叙述,未能表现出创造过程中的斗争、挫折,以及建立一个可观结构之前,数学家经历的艰苦漫长的道路.”[2]数学史是展示人类认识数学这一连续过程的最好媒介,它不仅追溯了数学内容、思想和方法的演变及发展过程,并且探索影响这种过程的各种因素[3].不同时期数学教科书中的方程定义及其演变,展示了人类对方程概念的认识过程,为今日教科书的编写和方程的课堂教学带来很多启示.因此,本文考察1820—1959年之间出版的120种美国和英国代数教科书中有关方程定义的内容,试图回答以下问题:美英早期代数教科书中是如何定义方程的?方程的定义是如何演变的?方程定义的历史对我们今天认识方程有何启示?对于今日方程的教学又有何启示?
2 研究方法
本文从有关数据库中选取120种美英早期代数教科书为研究对象.若以20年为一个时间段,则这些教科书的时间分布情况如图1所示.其中,对于同一作者再版的教科书,若内容无显著变化,则选择最早的版本,若内容有显著变化,则将其视为不同的教科书.
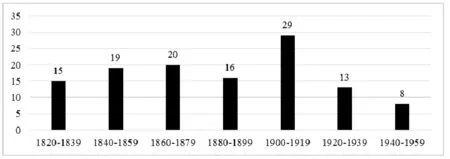
图1 120种教科书的时间分布
首先,按照年份查找并摘录出各教科书中的方程定义以及相关内容;接着,相关知识和文献[4],以关键词为参照,确定分类框架,根据文献[4]中所提,目前对数学概念的定义方式并没有形成共识,常见的提法有:属加种差定义法、发生定义法、形式定义法等.基于对方程定义表述方式的不同,本文首先建立初步的分类框架,运用该框架对早期教科书中的方程定义进行统计,再根据统计情况对分类框架进行适当修正,最终形成正式的分类框架(表1);最后,根据分类框架,对120种教科书中的方程定义进行分类与统计.

表1 方程定义的分类框架
3 早期代数教科书中的方程定义
方程作为一个数学概念,它是一种数学逻辑构造,是抽象逻辑的产物.本节根据分类框架对研究对象进行分类,属加种差定义、描述性定义和函数定义占比依次为8.27%, 90.08%和1.65%,其中描述性定义占比最大.
3.1 属加种差定义
属加种差定义法可以简单地表述为:被定义项 = 种差 + 邻近的属.在120种教科书中共有10种采用了此类定义方法,主要集中在19世纪末到20世纪初.表2给出了属加种差定义的典型例子.
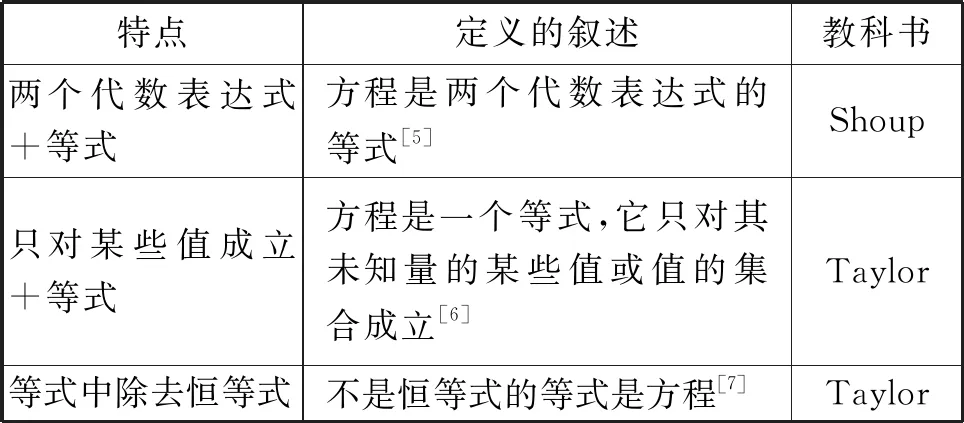
表2 属加种差定义的典型例子
3.2 描述性定义
描述性定义重在对方程形式的描述,共有108种教科书采用此类定义,占据压倒性多数.根据定义叙述的中心词,描述性定义又分为表达式、命题式、陈述法、比较法、典例法和组成法定义6种.图2给出了6种方法的分布情况.
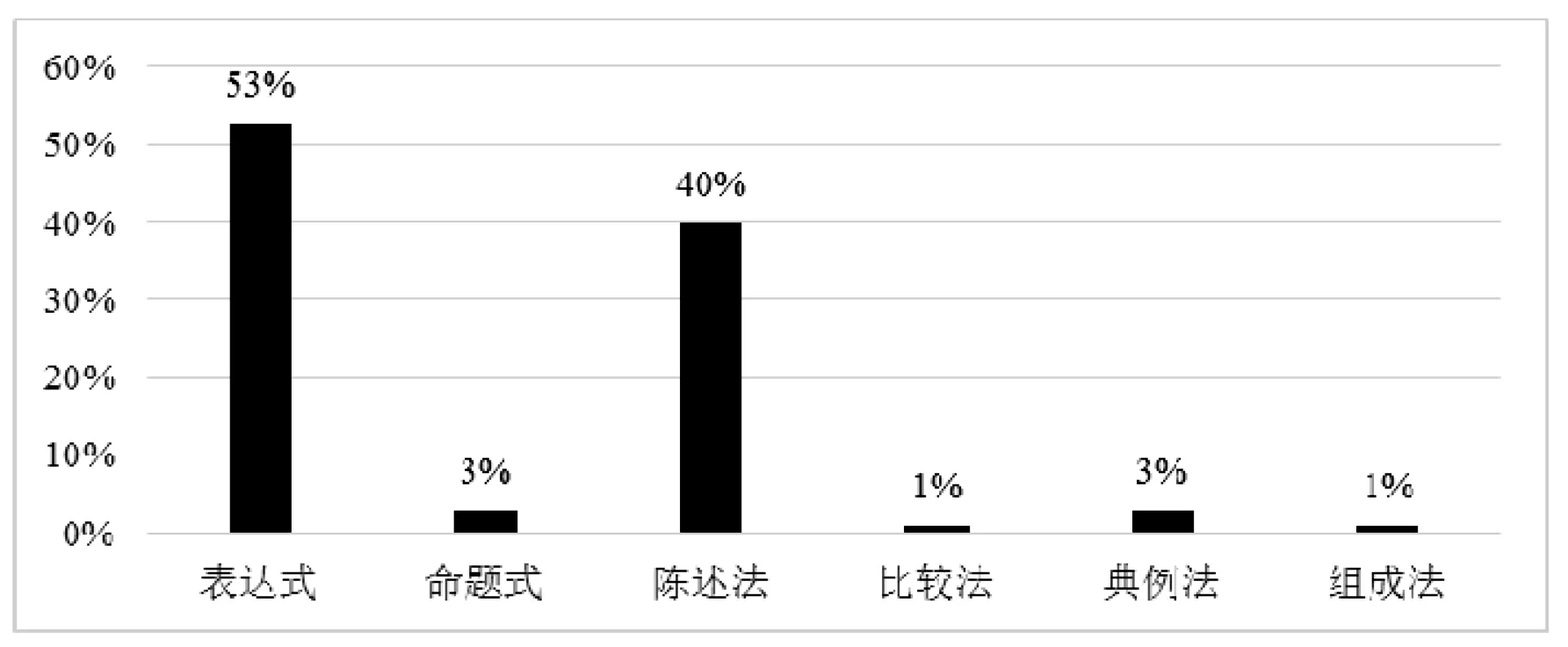
图2 各类描述性定义的分布情况
·表达式定义
将方程定义为等号连接的一种表达式的方法称为表达式定义,共有57种教科书采用此类定义方法.表3给出了表达式定义的典型例子.
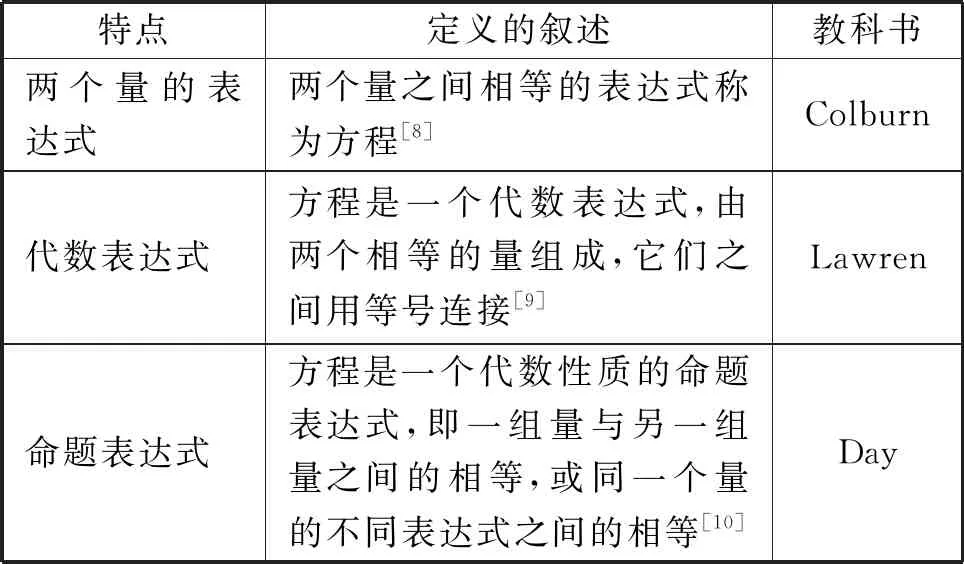
表3 表达式定义的典型例子
·命题式定义
中心词是命题的定义方式称为命题式定义.这种定义将方程看作一种命题.仅有3种教科书采用命题式定义的方法.表4给出了命题式定义的典型例子.

表4 命题式定义的典型例子
·陈述法定义
将方程定义为一种阐述、描述或陈述等的定义方式称为陈述法定义.共有43种教科书采用这种定义方式,在描述性定义方式中占比仅次于表达式定义.表5给出了陈述法定义的典型例子.

表5 陈述法定义的典型例子
·比较法定义
将方程看作是两个量之间比较的定义方式称为比较法定义.Williams将方程定义为“当两个相等的量用符号‘=’连接时,这种比较称为方程”[16].虽然仅有1种教科书采用此种定义,但是该定义值得关注,因为它将等号两边看作是地位平等的两个量,这有助于打破学生认为“=”仅代表运算结果的固有思维,从而更好地理解方程两边的等量关系.
·典例法定义
由典型的例子出发给出的定义称为典例法定义.共有3种教科书采用这种定义方式.如Hind将方程定义为“像ax+b=cx+d这样,符号‘=’两边的量彼此相等,整体称为等式或方程.”[17]Lilley将方程定义为“形如3x+5=5x-7的等式叫做方程.”[18]这种方式的特点就是从形式上说清楚“什么是”,但是忽略方程这一概念的本质.
·组成法定义
从方程的组成进行定义的方式称为组成法定义.在120种教科书中,仅有Ficklin采用这种定义方式,具体表述为“一个方程由两个用等号连接的表达式组成.”[19]
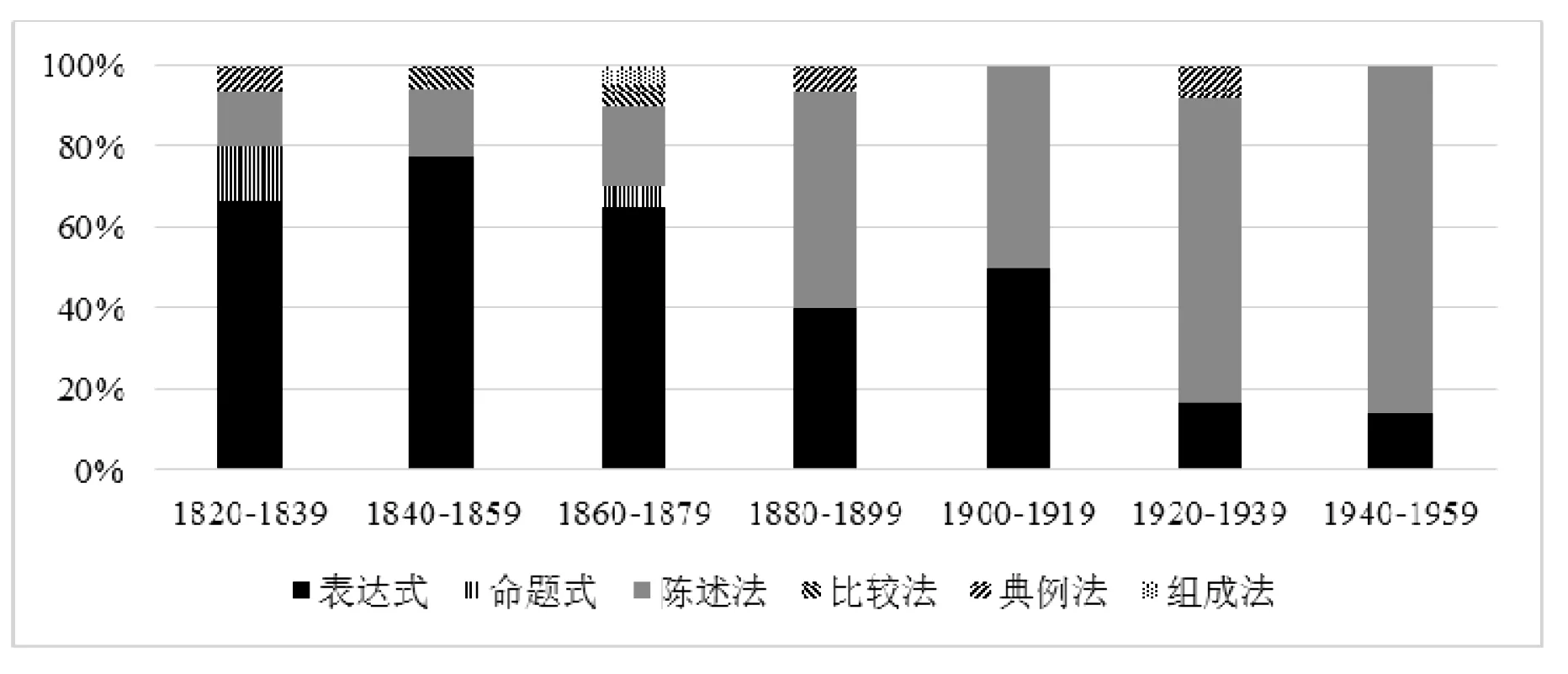
图3 6种定义方式时间分布
图3给出了上述6类描述性定义的时间分布情况.从图3可以看出,19世纪80年代之前表达式定义占有绝对优势,19世纪末占比开始减少.反之,陈述法定义的占比逐渐增加,到20世纪发展成为主流定义方式.而命题式、比较法、典例法和组成法定义都是在少数几个时间段昙花一现.
3.3 函数定义
从函数的角度来定义方程的方式称为函数定义.有2种教科书采用这种定义方式:Urner将方程定义为“要求x的一个值,使函数f(x)和g(x)具有相同的值,则f(x)=g(x)称为方程”[20],Whyburn将方程的定义叙述为“如果将含有一个或多个未知数的两个函数设为相等,并且对某些数而不是对所有值都成立,在这种情况下,它被称为条件方程.”[21]这种定义方式虽然在形式上将方程等号两边看作两个函数,但是这里的x不是函数中的变量,而表示未知数.20世纪初,德国数学家F·克莱因(F.Klein,1849—1925)提出以函数概念统一数学教育内容的思想[22],因此,函数定义法的出现受到了此种思想的极大影响.
4 方程与等式
在英语中equation这个单词本身就是等式的意思,数学里公式、函数、纯数字算式等都是等式的形式.120种教科书在定义方程时,有的将方程与等式进行了区分,有的则不加区分.具体主要分为以下三类.
第一类:未区分方程和等式.19世纪早期的教科书倾向于不区分方程和等式,部分教科书里明确表示纯数字的等式也是方程.表6给出了第一类定义的典型例子.
第二类:没有明确区分等式和方程,但明确说明方程含有未知数.第二类定义虽然没有明确区分方程和等式,但是提到“方程通常含有未知数”.这类定义在19世纪初占比最大,之后逐渐减少.表7给出了第二类定义的典型例子.
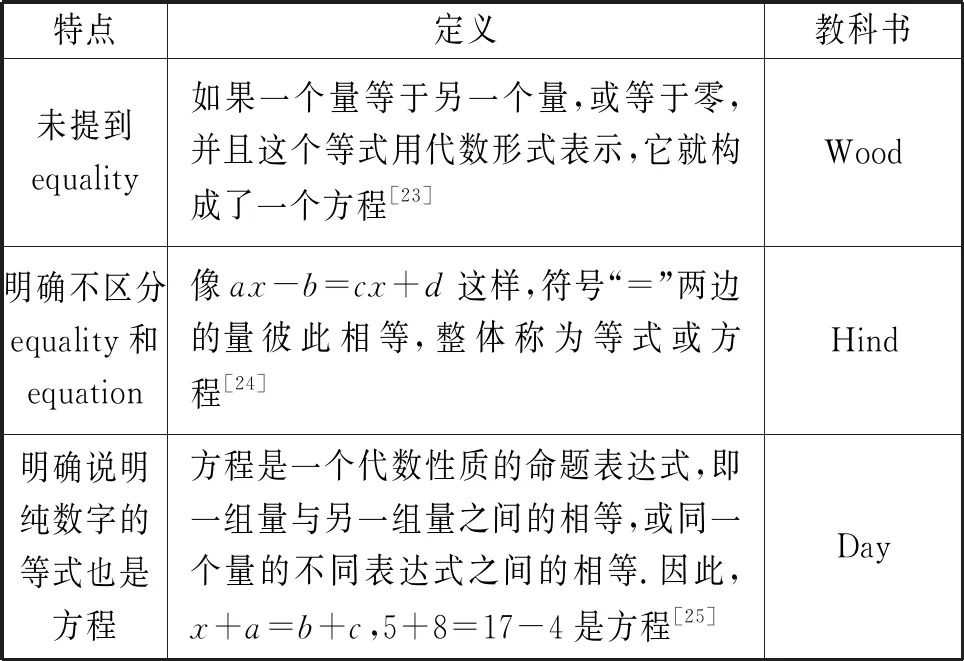
表6 第一类定义的典型例子
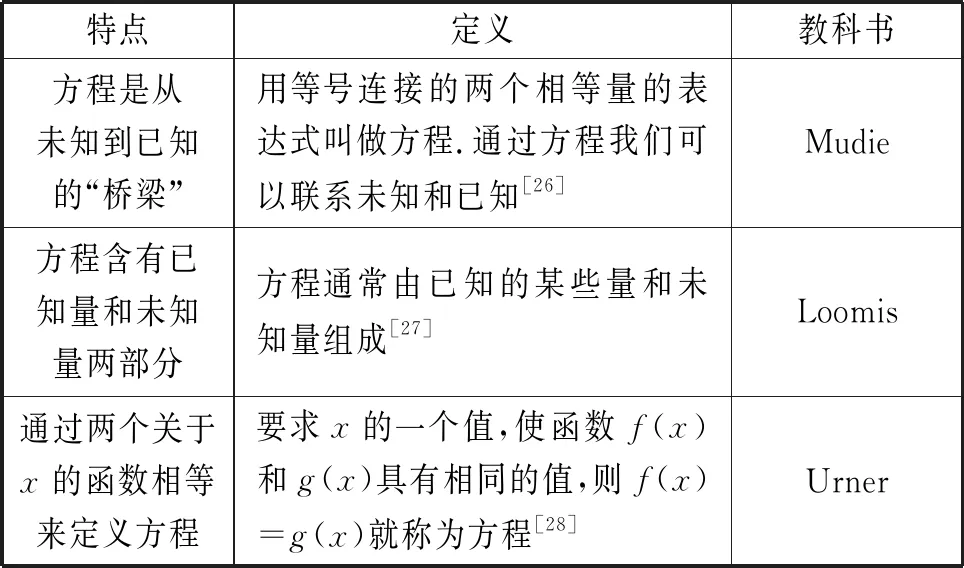
表7 第二类定义的典型例子
第三类:区分恒等式和方程.第三类定义突出方程包含未知数的特点,将方程作为等式的一种情形独立出来,强调只有某些特定值代入方程所含未知数后等式才成立,而通过已知部分和等量关系确定这些特定值进而求出未知数的过程就叫做解方程.表8给出了第三类定义的典型例子.
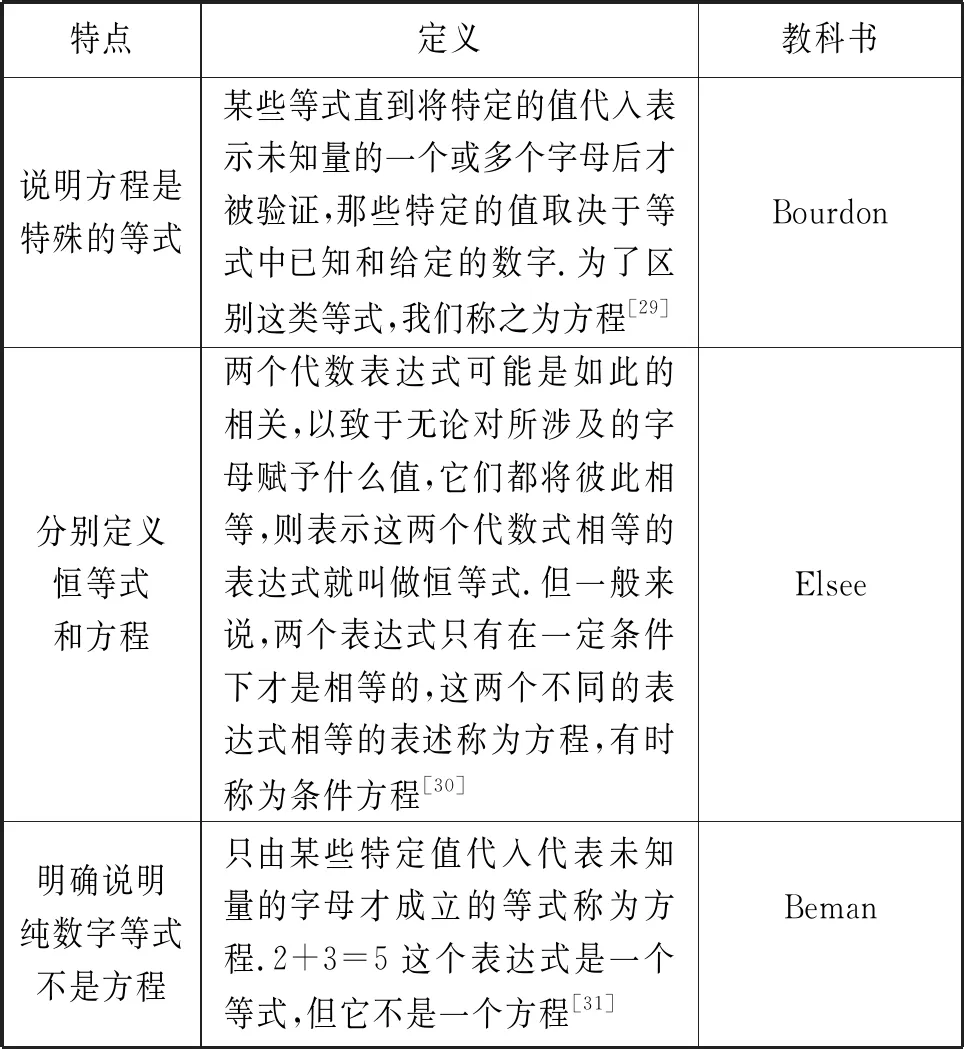
表8 第三类定义的典型例子
10个属加种差定义中,3个属于第一类,1个属于第二类,6个属于第三类.2个函数定义分别属于第二类和第三类.108个描述性定义中,39个属于第一类,20个属于第二类,49个属于第三类.若以20年为一个时间段,则上述三种方式的分布情况见图4.
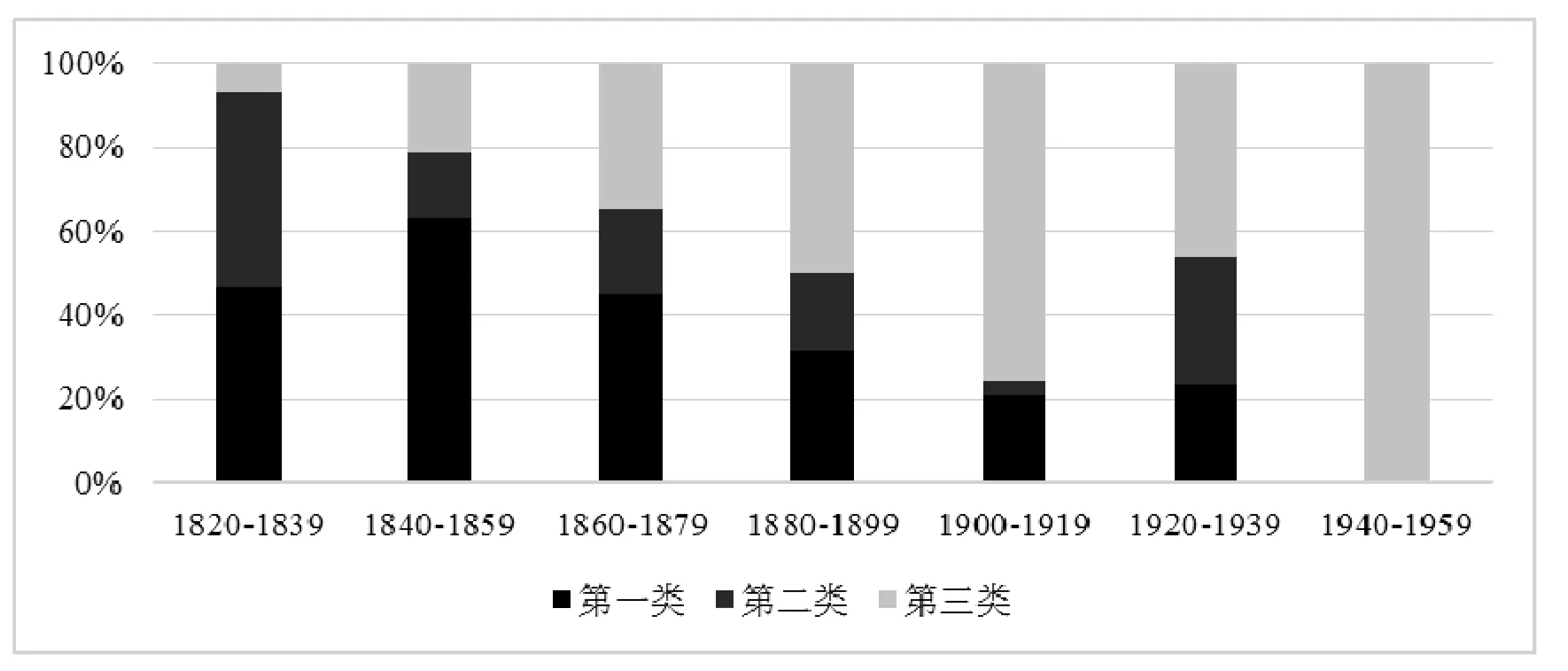
图4 120种教科书关于方程分类的时间分布
从图中可见,在19世纪初,第一类和第二类的占比较大,第三类占比最少.随后第一类在1840—1859年短暂增加后,开始逐渐减少;第二类的占比大体上也呈递减趋势,到20世纪中叶第一、第二类的占比都为零;第三类的占比逐渐增加,到20世纪中叶仅剩下这一种分类方式.早期的教科书并没有将方程和等式进行区分;随着时间的推移,教科书在定义方程时越来越倾向于强调“方程通常含有未知数”.进入20世纪,将方程与恒等式区分开的方式逐渐成为主流.
5 方程的意义
Bartoo & Osborne在“方程”章的开篇记载了这样一个故事,一个人在工作岗位上遇到了难题,在百思不得其解后,领导告诉他其实这就是他在学校里学习的代数[32].由此可见,方程不只是书本上的一个公式,更是解决实际生活问题的数学工具.
方程的本质体现在它将一个问题的已知部分和未知部分通过等号连接起来,并由此求出对我们有价值的未知数,进而解决实际问题.波利亚(G. Pólya,1887—1985)也曾说过:“方程的核心思想是借助一组等式关系求解未知数.”[33]
在所考察的120种教科书中,49种在给出方程的定义时,明确提到方程在求实际问题和数学研究方面的意义.例如Mudie将问题的已知部分和未知部分比作一条河的两岸,而得到它们之间的等量关系即建立方程,就是建造连通两岸的桥梁[26].Feinstein和Murphy则言简意赅地指出:方程本质上是一个问题,而不是一个陈述[34].
张奠宙先生也多次对教科书上关于方程的定义提出过质疑,并提议将方程定义为“方程,是为了求未知数,在已知数和未知数之间建立起来的一组等式关系.”[35]先生给出的定义非常严谨且清晰地揭示了方程的本质与意义,不仅符合西方代数教材中强调的等式关系,而且将求未知数这个功能说清楚了,同时也让学生明白方程不是一个自然存在的公式,而是建立数学模型的过程.
6 结论与启示
在120种美、英早期代数教科书中,共出现了属加种差、描述性和函数定义三类,其中描述性定义占比最大,又可具体分为表达式、命题式、陈述法、比较法、典例法和组成法6个子类.19世纪80年代之前,表达式定义占有绝对优势,随后陈述法定义的占比逐渐增加,到20世纪发展成为主流定义方式.同时,方程的定义也经历了从模糊到清晰的过程,早期的教科书倾向于不区分方程和等式,到19世纪末,方程才逐步从等式中独立出来.从本质上来说,方程是一个问题,它的意义在于通过等量关系连接问题的已知和未知,进而求解未知数,方程的建立是一个数学建模的过程.
早期教科书中方程定义的多样性以及方程定义的演变过程可以为今日教学提供有益的参考.
首先,早期教科书给出的一些定义或观点有助于我们澄清有关方程定义的争议.例如,无论按照何种定义,x=1当然是方程;但按照Feinstein和Murphy的观点“方程本质上是一个问题,而不是一个陈述”[34]以及Smith的观点“我们可以把条件方程看作疑问句,它询问在什么条件下这个等式是成立的”[36],x=1是一个陈述——即未知数等于1,而不是一个问题——x等于多少时等式成立,因而可以说它不是真正的方程.至于x+1=x+2,根据比较法定义,它是一个不等关系,并不属于方程.
其次,方程概念从不完善到完善的演进过程为今日HPM视角下的方程概念教学提供了参照.教师可以设计教学活动,让学生在课堂上用自己的语言给方程下定义,并进行古今对照,从而促进学生对方程概念的理解.教师可以引用早期教科书的精彩观点,如“方程是沟通已知与未知的桥梁”,让学生感悟数学对于人类认识世界的价值,彰显数学的文化之魅.教师还可以制作以“方程定义的历史”为主题的HPM微视频,让学生感悟数学概念的演进过程,树立动态的数学观,达成德育之效.
