目标引领差异分析 类比猜想揭示本质
——新课程视角下一道习题的教学活动及思考*
2020-12-03邓迎春江苏省仪征中学211400
邓迎春 (江苏省仪征中学 211400)
习题是数学知识的载体,是数学思想方法的生长点,蕴涵着巨大的教育潜能.如今,新一轮基础教育课程改革正在积极推进,新课程理念强调对学生数学能力的培养.然而,当前习题课存在诸多问题,特别是教师讲解采用“一言堂”的模式,就题论题,直指习题的正确解法或答案,严重忽视学生多方面数学能力的培养,更别说促进学生学会学习了.那么,在新课程视角下如何开展习题教学呢?最近,笔者对一道测试题进行了研究并开展了教学活动,深有感悟.
1 试题呈现及答题调研分析
1.1 题目和参考答案
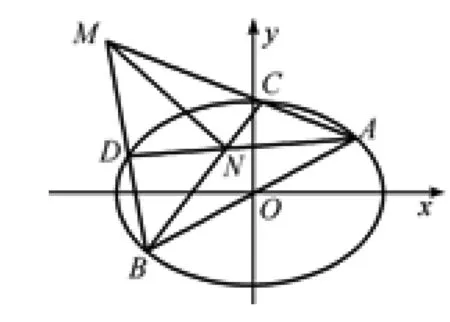
图1
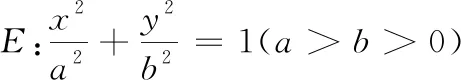
(1) 求椭圆的方程;
(2) 求证:直线MN的斜率为定值.
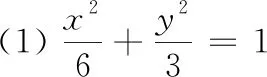
(2) 由(1)知A(2,1),B(-2,-1).
①当AC,BC,AD,BD的斜率都存在时,设直线AC,AD的斜率分别为k1,k2,C(x0,y0),显然k1≠k2.
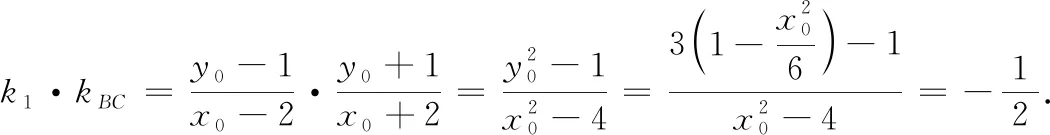

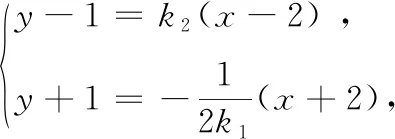
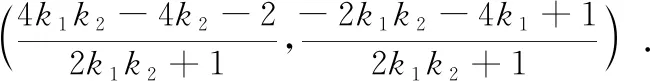

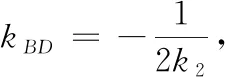
综合①②可知,直线MN的斜率为定值-1.
1.2 答题调研分析
笔者上课班级是南京师范大学第二附属高级中学实验班,全班共54人,学生有一定的分析问题和解决问题能力.第(1)问学生答题情况较好;但第(2)问(计10分)得分率较低,只有2人答对,平均得分率仅为3.1分.
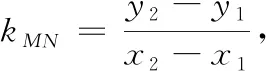
笔者查阅相关资料后发现此题是南京市2015年一道高考模拟试题.命题者的命题意图是什么呢?命题的背景又是什么呢?通过对这道题的深入研究,发现这道题不仅考查了解析几何题解题的常规思路,更蕴含着丰富的数学思想方法和数学背景.笔者认为这道题不能简单评讲、一带而过,有必要用一节课来引领学生去探究解题思路,追根溯源揭示本质,充分发挥本题的功能和价值.
2 教学实录
课前(提前一天)将参考答案发给学生,要求学生认真研读,并能独立讲述解题思路,积极探索其他解法.
教学片段1自主学习,交流心得
师(简单介绍本题的得分情况后):已要求大家研读了本题的参考答案,谁能讲述一下解题思路呢?
生1:目标实际上就是求直线MN的斜率,而直线MN的斜率与点M,N的坐标有关.设直线AC,AD的斜率分别为k1,k2→找到直线AC与BC斜率及直线AD与BD斜率的关系→写出直线AD的方程和直线BC的方程→求出交点N的坐标→同理求出M的坐标→求出直线MN的斜率→验证斜率不存在的情况→下结论.
师:讲得很完整,课前下了功夫,理解了本题的解法!现在请大家想一下,你们都经历了本题的求解过程,有哪些体会和想法?
生1:我觉得,本题是直线与椭圆的综合应用问题,要注意分类讨论,不能漏考虑AC,BC,AD,BD中有直线的斜率不存在的情况.
师:生1告诉我们要注重细节,追求完美.还有吗?
生2:考试时,我设了AC,BC,AD,BD这四条直线的斜率,求出M,N的坐标,较复杂,没能进行下去.通过研读参考答案,我觉得本题中对椭圆的第三定义熟知的话,就能找到直线AC与BC斜率及直线AD与BD的关系,有助于解题.
师:你说的椭圆的第三定义是什么?
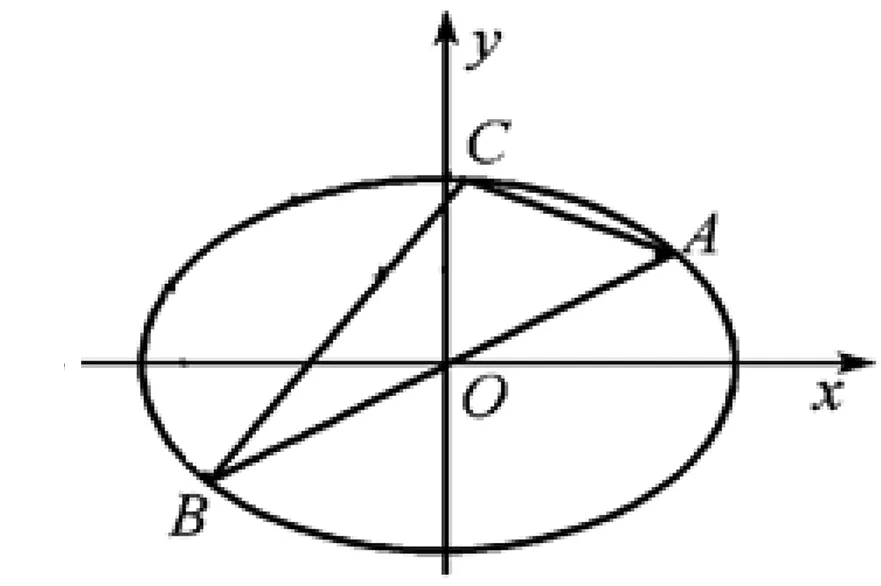
图2
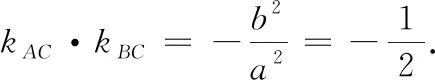
师:你说的这一结论除了参考答案中的证法,还有其他证法吗?
生2:可以设出AC的点斜式方程,和椭圆联立方程组,求出点C坐标,再求出BC的斜率就可以了.
师:生2 说得很好,此法虽然略繁,但也是常规方法.生2 还告诉我们,如果熟知一些常用数学结论的话,有利于我们打开解题思路,所以在平时的学习中要多注意反思总结.当然,在解题中用到时应给予适当证明,应知其来龙去脉.
教学片段2差异分析,驭繁为简
师:同学们,还有什么感受吗?
生3:我觉得这个参考答案思路是容易理解的,但计算太繁,总是算错,能不能有更容易计算的方法呢?
师:对呀!怎一个“繁”字了得!(学生大笑)
师:谁有什么好的念头或建议吗?
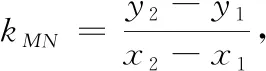
师:从目标入手,不错的想法!目标所需要的能从条件中找到吗?如果不能得到,你能从条件中得到什么?
师:是吗?大家一起思考一下!我们的目标一定要解出x1,y1,x2,y2吗?
生众:可以求出x2-x1和y2-y1这两个整体就可以了.
师:大家想法不错,尝试一下!
生5(一会儿后):x2-x1和y2-y1这两个整体也不能求出!只要找到x2-x1,y2-y1这两个整体的倍数关系就可以了.因此可以将(*)式化为
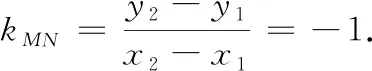
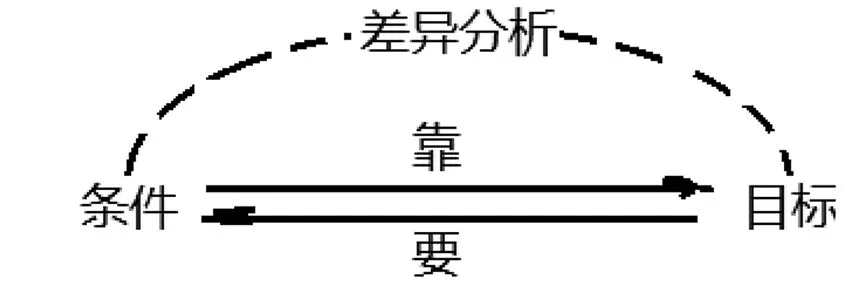
图3
师:太好了!这种解法极大地简化了运算.大家再回顾一下,这种解法是怎么来的?我们能得到怎样的解题经验?(此处停留1分钟)我来帮大家总结一下:紧扣目标,转化条件,差异分析!(板书图3,并讲解目标引领、差异分析的方法)
教学片段3类比猜想,揭示本质
师:这道题我们已经优化了解法.大家还有什么疑问或想法吗?
生6:直线MN的斜率为什么是定值呢?是不是有什么潜在的规律呢?
师:发现问题比解决问题更重要,生6给我们提出了一个值得探究的问题!大家思考一下,直线MN的斜率为什么是定值呢?

师:同学们不要笑,生7无疑给我们指明了一个方向!那就是直线MN的斜率是由椭圆和直线确定的.那么怎样确定呢?之前,我们遇到过类似的定值问题吗?
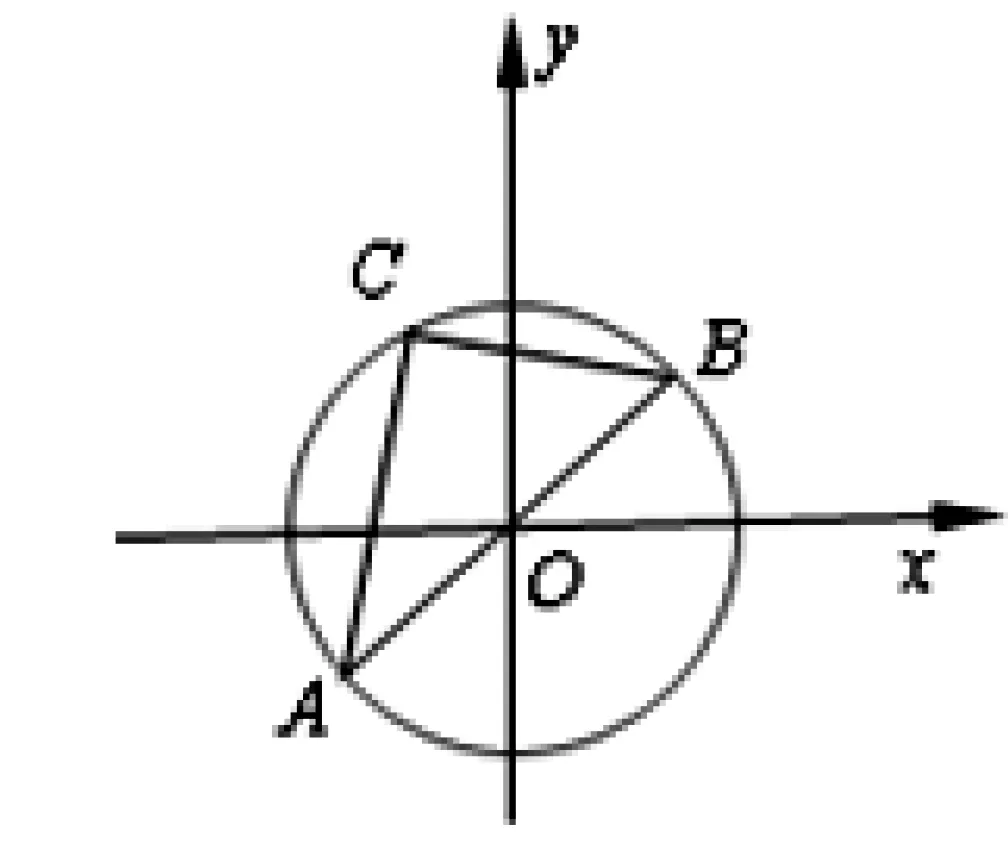
图4

师:说得很好!椭圆可以认为是由圆变换得到,圆中的很多结论在椭圆中也可能有着类似的结果.现在大家按生8的方法尝试一下,将图1中的椭圆改为圆,看会有什么发现?
(学生深受启发,都投入到动手画图探究之中)

图5
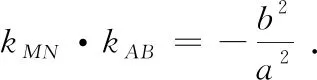

(学生又投入证明探究之中)
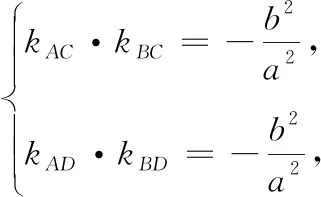
师:大胆猜想,小心求证!我们通过类比猜想证明了这样一个新的结论,拓宽了我们的眼界.
教学片段4合作探究,形成经验
师:通过刚才的猜想证明,我们获得了什么基本经验?
生11:通过对圆中一些结论进行类比,可以得到椭圆中相应的结论.
师:说得很好!以后遇到椭圆中的一些定性问题处理有困难的话,不妨将其退化到圆中进行类比猜想,或许能打开解题的思路.现在,大家互相讨论一下,能不能再举一些由圆类比到椭圆的例子?
经过学生的讨论,类比猜想出以下两组命题:
(1)命题1 如图6,在平面直角坐标系xOy中,斜率为k1的直线与⊙O:x2+y2=r2交于A,B两点,直线AB的中点为M,若OM的斜率为k2,则k1·k2=-1.
通过类比猜想得到
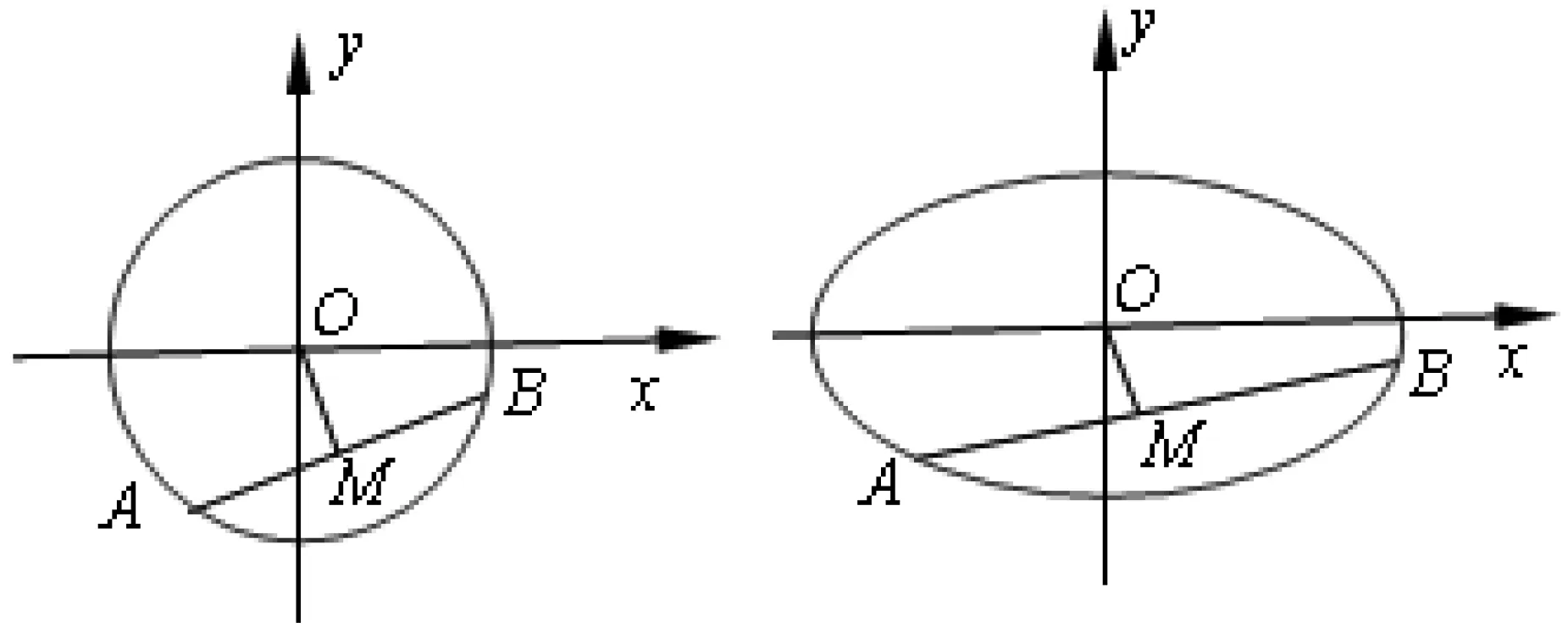
图6

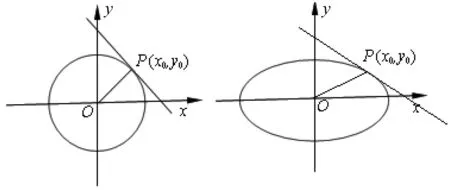
图7
(2)命题3 如图7,在平面直角坐标系xOy中,斜率为k1的直线与⊙O:x2+y2=r2相切于点P,若OP的斜率为k2,则k1·k2=-1.
通过类比猜想得到:
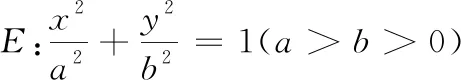
(由于时间关系,让学生证明了第(1)组命题,第(2)组命题由让学生课后去尝试证明)
教学实录5总结提炼,提升素养
师:通过这道试题的研究学习,同学们有何收获呢?请大家尝试画出认知网络图.
引导学生不断完善图8中认知网络.
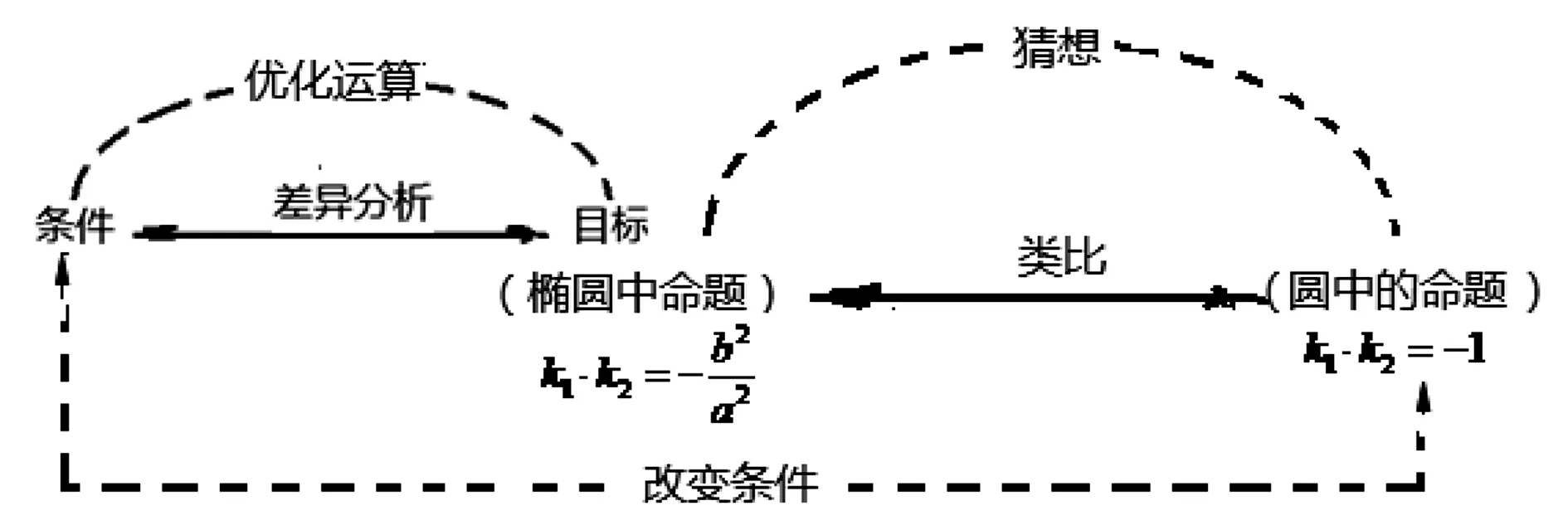
图8
师:(投影课后挑战问题)请大家课后证明图7中猜想的结论,并思考如下的挑战问题,撰写本节课的心得体会.期待你们的成果!
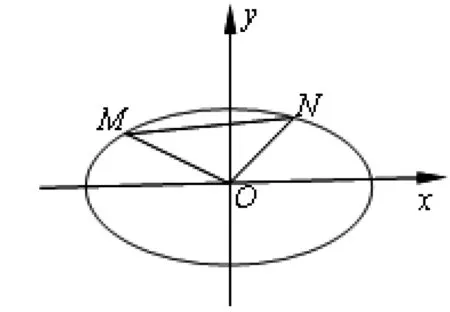
图9
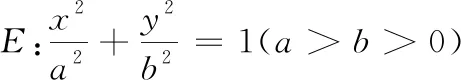
3 课后访谈调研及学生后续探究
鉴于这是一节研究课,笔者课前邀请了几位同行来听课,课后和这几位教师进行了交流.同时为了解学生通过本节课的学习感受,对学生进行了问卷调查.
3.1 对教者的访谈
笔者:谢谢你们听了我这一节研究课,烦请说出真实的听课体会.
师1:我所任教班级学生在本题第(2)问上得分率也很低,之前我认为此题思路是常规的,学生只是运算能力欠缺,因此评讲时仅仅对照参考答案给学生分析了一遍.听了你的课后,才明白学生运算能力的提升不仅要帮学生理解运算的对象和运算法则,更要引领学生探究运算的方向、选择运算的方法.
师2:我感叹听了一节“真数学课”,很有数学味.这节课以一道试题为资源引领学生探究解法,通过类比揭示蕴含的数学规律和本质,有利于教会学生数学地思考.
师3:从课堂上学生的表现可以看出,学生不断陷入“痛苦”的思考,又不断体验到成功的快乐.学生在问题驱动下自始至终积极参与、交流互动,充分享受着数学的美.
师4: 授课者针对学生的答题情况,始终基于学生的已有经验进行有效的提问,通过问题激起新的“矛盾”,从而让学生探究得到新经验.
3.2 对学生的调研分析
为了便于对学生调研,笔者设计如下的问卷发放给学生,共发放54份,收回54份.
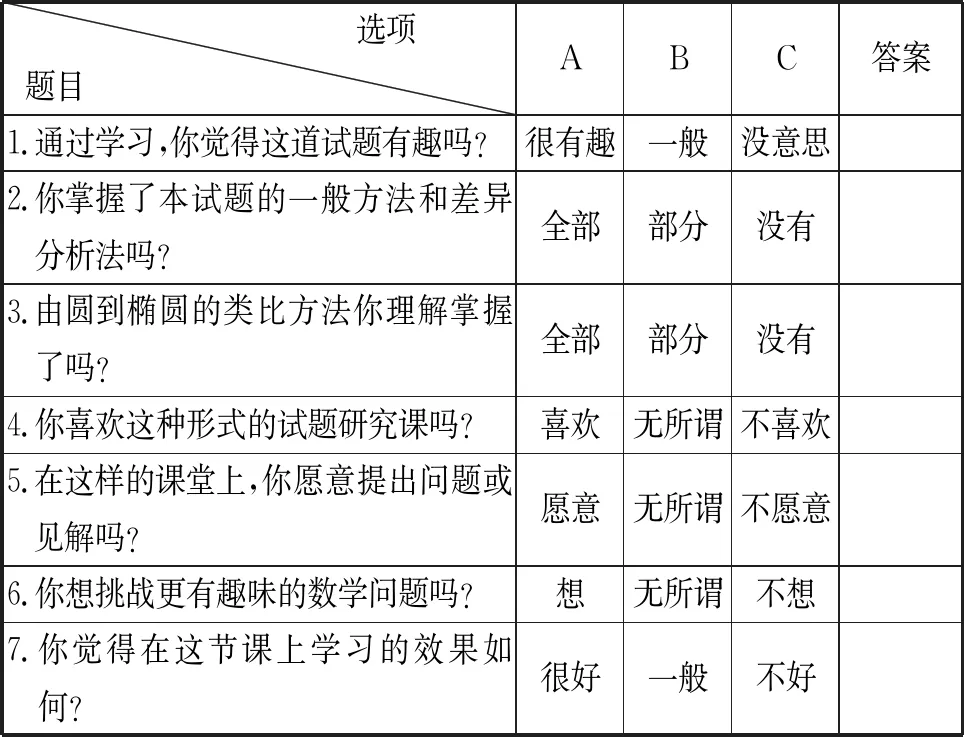
选项 题目ABC答案1.通过学习,你觉得这道试题有趣吗?很有趣一般没意思2.你掌握了本试题的一般方法和差异分析法吗?全部部分没有3.由圆到椭圆的类比方法你理解掌握了吗?全部部分没有4.你喜欢这种形式的试题研究课吗?喜欢无所谓不喜欢5.在这样的课堂上,你愿意提出问题或见解吗?愿意无所谓不愿意6.你想挑战更有趣味的数学问题吗?想无所谓不想7.你觉得在这节课上学习的效果如何?很好一般不好
经统计分析上表中的这7个问题,选A率分别为94%,87%,98%,96%,83%,85%,90%,可以得出这样的结论:学生喜欢这样的课堂,不仅是有收获的,而且是有趣的、有数学味的,学生学习数学的热情得到了激发.
另外,课后仍有学生来和我交流他们后续的研究成果.我和他们交流后,让他们整理好成果张贴在教室里并在自习课上讲给其他学生听,这一方面能提高学生的数学表达和交流能力,另一方面也让其他学生有所收获.在和学生交流的过程中发现,学生对数学学习的热情和获得成功的喜悦溢于言表.
4 思考
4.1 目标引领差异分析,提升数学运算素养
《普通高中数学课程标准(2017年版)》提出了数学学科六大核心素养,其中包括数学运算.然而数学运算是教师教学的“痛点”,学生学习的“惧点”.数学运算能力的现状是:学生面对数学问题一看就懂,一听就会,一算就错.这就说明学生是能理解运算对象和运算法则的,但是有时不能探究出合理简洁的运算思路和运算方法,导致运算复杂,会而不对.作为数学教师,如何指导学生改变运算能力现状,提升学生数学运算素养呢?无疑“目标导向,差异分析”是帮助学生探究解题方向,简化运算的一个重要策略.任何一道数学题目都有“条件”和“目标”两个信息源,并且这两个信息源之间总有差异.从目标发出的信息预告需知并诱导解题方向,从条件发出的信息预示可知并启发解题手段.我们只需借助一些图形或记号等对这些信息进行分析、加工,进而在两者之间建立联系(即消除差异).分析、加工时,通常可以思考这样一些问题:本题的目标是什么?得到这个目标需要什么?本题的条件是什么?根据这个条件能够得到什么?目标和条件之间有什么差异?如何消除这些差异?这样对目标进行集中导向,对条件进行发散处理,从而只要数种方案中有一种能够沟通(即消除差异),问题即可获解.这一解题策略概括成口诀就是下面的两句话:目标诱导方向(明确我要干什么),条件启发手段(分析我已经知道什么);实施差异分析(关注目标与条件之间有何差异),有效整合信息(寻求合适的路径消除上述差异).本案例教学片段2中,就是在学生理解了一般解法的基础上,借助学生的经验,利用“目标导向,差异分析”引领学生探究出简明快捷的解题方向和思路,驭繁为简,提升了数学运算素养.
4.2 类比猜想揭示本质,培养学生发现问题的能力

4.3 丰富形式增强实效,促进学生学会学习
《普通高中数学课程标准(2017年版)》在教学与评价建议中指出,教师要把教学活动的重心放在促进学生学会学习上,教师要善于根据不同的内容和学习任务采用不同的教学形式,优化教学,抓住关键的教学与学习环节,增强实效.本教学案例中,改变了常用的试题评讲的形式(如访谈中师1的教学形式),在课前让学生自主学习本试题的参考答案,理解其中的知识和技能,培养了学生的自学能力;在教学片段1中让学生简要讲述解题的思路,并提出困惑和体会,培养学生的思维和表达能力;在教学片段4中让学生合作探究出两组圆与椭圆的类比命题,在教学片段5中引领学生尝试画出认知网络图以及让学生课后思考并撰写心得体会,培养了学生的交流与反思的能力等.如此从课前、课中、课后努力丰富了学生的学习形式,正如访谈中师3所说的学生不断陷入“痛苦”的思考,又不断体验到成功快乐,学生在问题驱动下自始至终积极参与,交流互动,充分享受着数学的美.由课后学生调查及学生反思的心得体会情况来看,教学效果是明显的,也正如师4所说的基于学生的已有经验,通过问题激起新的“矛盾”,从而探究得到新经验.教学中充分体现了数学学科素养的四个方面,即“情境与问题、知识与技能、思维与表达、交流与反思”,也是学会学习的必备条件.
