HPM视角下三角学序言课教学实践探索
2020-12-03何晓蕾浙江省义乌市第五中学322000
何晓蕾 (浙江省义乌市第五中学 322000)
序言课在高中数学教学中占据着重要地位,在了解知识背景、理解知识脉络、指导学习方法等方面起着重要作用.但如果序言课仅仅是浅层内容的堆砌,就会变成一节普通的概念课,如果为了吸引学生的关注而变成一节“故事课”,则达不到序言课的教学价值最大化.唤醒学生的已有认知,揭示知识学习的必要性,解决学生的“顽固性疑惑”,实现数学史的多元教育价值是序言课的使命.鉴于此,笔者从HPM视角就“三角学序言课”进行了教学实践探索.
1 相关历史材料及其运用
高中三角学包含三角函数、三角恒等变换和解三角形,学生在学习这部分内容时会产生一些顽固性疑惑,比如:初中已有了角的概念,为何要重新定义任意角?角度制已经如此深入人心,为何非要引入弧度制?这些核心概念在教材中并没有解释清楚,而教师因为课时紧张等原因也没有在课堂上解决学生的困惑,序言课就担负了这个使命.同时,三角学的历史发展也为解决上述教学问题提供了重要参考.
三角学萌芽于天文学,是测量计算的工具.最早,为了计算地球与太阳旋转中心的距离,希腊数学家西帕霍斯引入了弦表——在半径固定的圆中,求给定弧长所对的弦长[1].他默认当圆的半径不变时弧长和角度有一一对应的关系,因此在计算时,圆的弧长和半径采用和角相同的六十进制度量方法,这便是弧度制的雏形.历史告诉我们,三角学的萌芽阶段无声地孕育着函数的思想和弧度制的思想.之后,数学家们在对圆的研究中引入了余弦、正切、正弦的概念,也推导了许多三角学公式[2].只是,弦表的研究重点仍是给定半径时弧与弦的对应关系,函数思想也仍停留在表格形式.直到14世纪,数学家雷提库斯发现给定半径时角的大小和弧长是一一对应的,于是脱离了圆这个工具用直角三角形的边长比来定义正弦、余弦等概念,从此角成了正弦函数的自变量.17世纪,数学家们引入了“函数”概念,三角学的重点从强调计算转变为强调函数方法,三角学从研究三角形的边角关系转换为研究现实世界中具有周期性的运动变化.只是此时度量长度的单位已是十进制,而角度是六十进制,进位制的不统一使得弦表难以体现其便捷性,新的度量单位即弧度制应运而生,半个周期的正弦曲线也面世了.事实上,弧度制产生的直接原因是为了解决进位制不统一问题,更深层的是当时的时代背景.三角学脱离了三角形,数学家们用解析思想研究三角函数,是研究函数图象及性质的需要,这也和19世纪芝加哥三角教科书中对弧度制的教学安排不谋而合[3].
鉴于此,在三角函数的教学中,笔者从现实生活入手,为了刻画生活中周而复始的运动变化而引入任意角;从函数思想入手,为了画出正弦函数的图象而不得不考虑变更度量单位,引导学生引入弧度制.
2 课堂教学实录
2.1 发现正弦定理
师:(展示古希腊数学家埃拉托色尼测量地球周长的故事)同学们有没有想过自己去测量月亮到地球的距离?
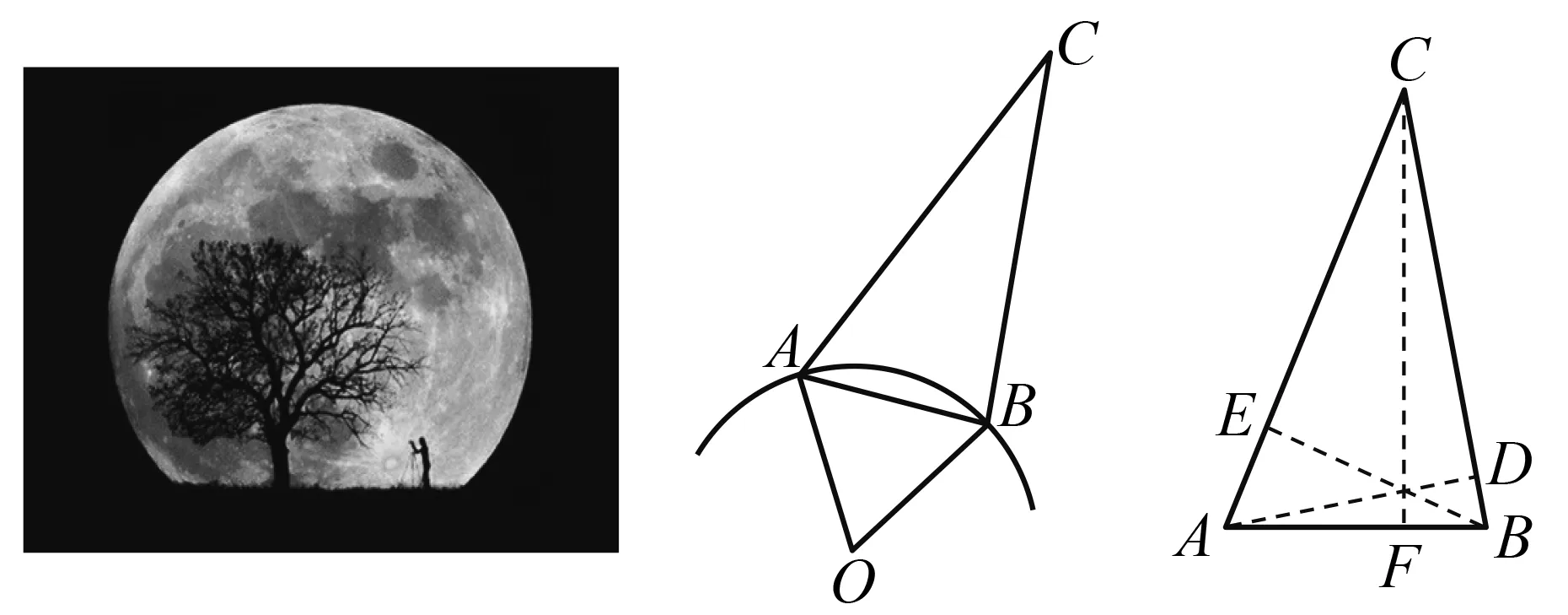
图1
师:图1为某兴趣小组测量超级月亮的示意图,O为地球球心,两人分别站在A,B两点同时观测月亮C,测量计算出AB两地的直线距离,以及∠CAB和∠CBA,求超级月亮C与A,B两地的距离.
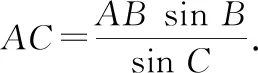
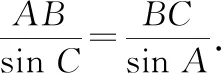
师:很棒,这个公式我们称为正弦定理.公元2世纪,古希腊天文学家托勒密在圆中发现了正弦定理,18世纪英国数学家哈里斯就是采用构造直角三角形法证明了正弦定理.那么钝角三角形满足这个定理吗?三角形中还存在其他数量关系吗?我们将在必修5第1章中学习,可以更全面地得到三角形中的边角关系,可谓有“棱”有“角”.
2.2 感受弧度制
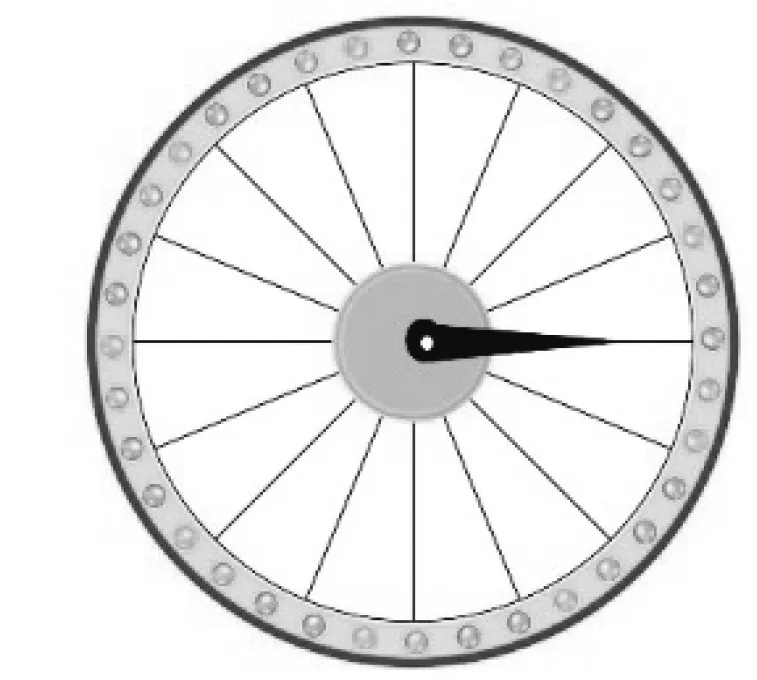
图2
师:17世纪以前的主流三角学被称为几何三角学,通过几何运算研究静态的三角形边角关系.17世纪以后,数学家欧拉转移了大家的视线,用函数视角研究生活中一些具有周而复始变化规律的匀速圆周运动,比如力学中的弹簧、钟摆、大提琴等.大家觉得哪一个量可以刻画这种周而复始的运动变化(图2)?
生:如果以指针停留的位置为基准,角的大小变化可以用来刻画周而复始的状态.
师:这个角和大家初中学的角一样吗?
生:不太一样,这个角是动态角,旋转形成.初中的角是静态的平面图形,而且旋转角的范围可以超过360°,和初中角的范围也不一样.
师:旋转角有方向的区分.我们规定逆时针旋转为正角,顺时针旋转为负角,不做任何旋转为零角.
师:有了角的定义,数学家们开始研究角的函数.回忆我们当初研究基本初等函数模型的一般步骤,大家说说如何研究三角函数?
生:研究函数需要研究定义域、值域、图象、奇偶性、单调性,也可以作出图象研究函数的性质.
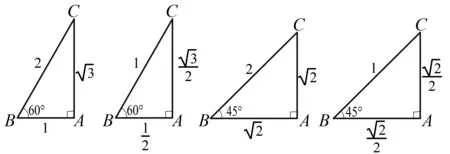
图3
师:画图解决的是横、纵坐标的关系,请大家用几何图形画出sin 60°, sin 45°.(学生作图,教师巡视,并挑选出有代表性的图象予以展示,如图3)
师:综合这些图象,哪一类形式的三角形更适合统一?
生:斜边长为1时更好统一,根据正弦函数的定义,任意角度对应的直角边AC即为这个角的正弦值.
师:取遍所有锐角,这些密集的点C最终形成了什么?
生:应该是半径为1的圆的四分之一圆弧长.
师:总结得很好.我们将半径为1个单位长度的圆叫作单位圆.当我们取任意锐角时,这个角的正弦值就是y值,也就是单位圆上点的纵坐标.如此我们解决了函数图象的纵坐标问题,现在大家可以画出y=sinx的图象了吗?
生:在x轴上取出1°的单位长度,把对应的正弦值标在坐标系中,所有点连成的曲线就是正弦图象了.
生:不对,1°的单位长度不同,所画出的图象也是不一样的.这样正弦曲线不是有无数个了?(学生们纷纷点头表示同意)
师:这位同学的疑惑很有道理,归根结底还是坐标轴上自变量和因变量的单位长度不一致,和数学家们当初想的一样.那么改变角的度量单位刻不容缓!我们刚刚用几何图形表示了正弦值,能否用几何图形来表示角的大小呢?(教师略顿,看学生一时没有思路,稍稍提醒)在指针的旋转过程中,随着角的大小变化,哪些量发生了变化?
生:弧长、弦长、面积.这三个里面弧长更直观一些,可以考虑用弧长表示角的大小.
师:大家认为角越大弧长也越大吗?
生:应该说在半径固定的圆中角越大弧长越大.可以设半径长度为1,就是单位圆.这样就可以用角所对的弧长来表示角的大小了.
师:厉害!当时的数学家们也发现了给定半径时角的大小和弧长是一一对应的.这样正弦函数y=sinx的自变量可以用什么表示了呢?
生:角x在单位圆中所对的弧长.
师:自变量和因变量都可以在坐标系中表示了,现在大家可以利用这个转动的圆盘画出正弦函数图象了吗?

图4
两位学生上台合作(图4),用可弯曲的磁条标出15°所对角的弧长为横坐标,再量出角所对的垂直距离为纵坐标,描出各点连成曲线就是y= sinx在0°~90°内的图象(图5).
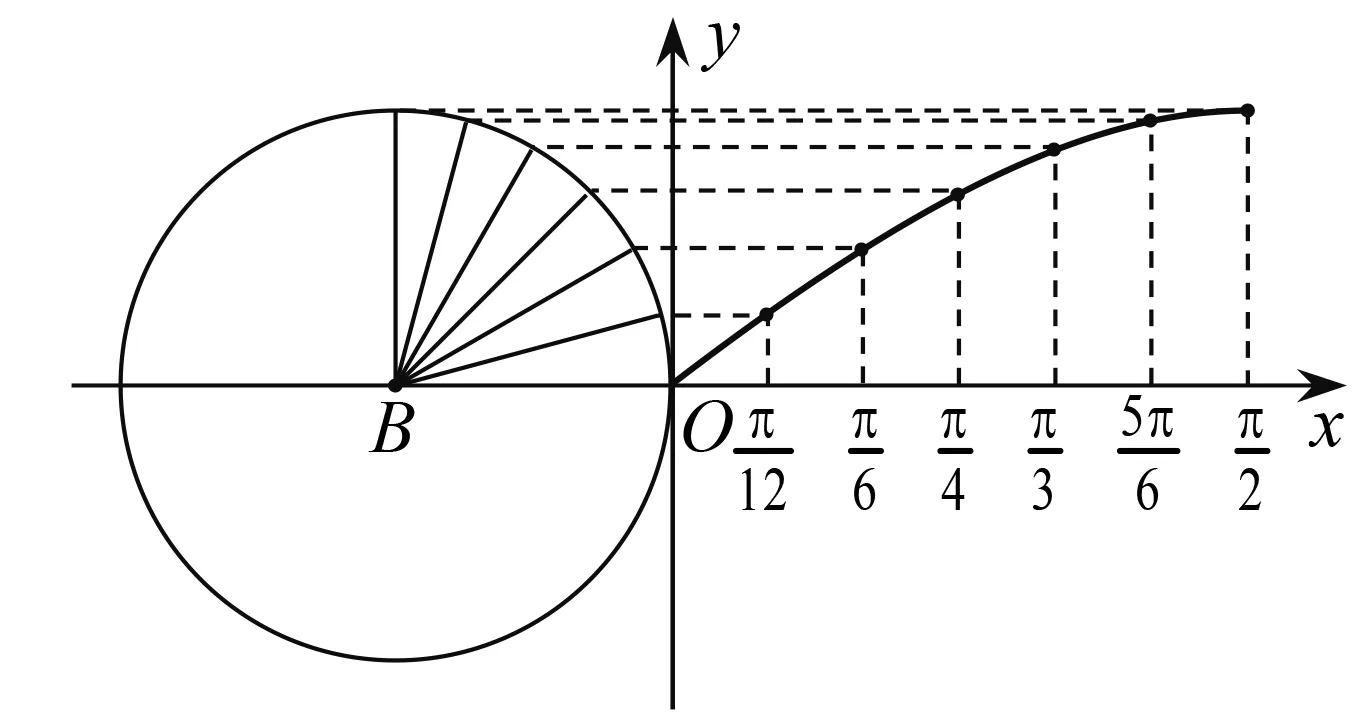
图5
师:用长度度量角的大小的方法叫作弧度制,是除了角度制之外又一个度量角的方法.大家可以根据以上过程表示出角度和弧度之间的等量关系吗?
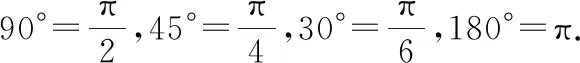
师:恭喜大家揭开了角度制与弧度制的奥妙!引入弧度制完美地解决了用角度画正弦图象存在的问题.用动态的视角、函数的工具来研究高中三角函数,可谓是别有“动”天.
2.3 探究两角差的余弦公式
师:三角函数研究的是“一个角”的函数,那么两个角的三角函数表达式应该是怎样的呢?例如,cos(x-y)=cosx-cosy吗?小组合作探究结果.(教师巡视,察看学生的讨论思路和结果)
生:这个式子不对,当x=y时,等式左边为1,等式右边为0.
生:通过代入特殊角发现cosx, cosy的差、和、积、商、幂都不能表示cos(x-y).
生:取x=60°,y=30°,可以发现cos(x-y)=cosxcosy+sinxsiny.
师:大家的讨论和思考都很有道理.数学是一门严谨的学科,不仅要大胆猜想,还要小心论证.
3 学生反馈与教学反思
本节课的授课对象是义乌市某普通高中的高一学生.课后,笔者采用问卷和访谈两种方式,就学习情感、内容理解、思想方法等方面对学生进行调查.
(1)学习情“”感上,82.6%的学生表示很喜欢这节课的内容,认为在上新课之前上这样的序言课是非常有必要的,融入数学史增添了趣味性和人文性,理解了三角学与现实生活中的重要作用,了解到知识产生的过程中数学家们的思考,特别是当自己的思考和数学家们不谋而合时有特别大的成就感.
(2)内容理解上设置的问题是:高中三角学包含了哪些内容?哪些内容和你以往的理解不一样?为什么高中教材先学三角函数?部分学生能说出高中三角学包含解三角形、三角函数和三角恒等变换三部分内容;和初中的知识相比较,初中角和高中角的定义不同,高中角是动态的、旋转形成的,有方向的区别,角度制和弧度制是两种不同的度量单位,想要画出正弦函数图象就必须解决进位制不统一的问题;先学三角函数应该是为了统一高中对角的定义,这样三块内容才能成为一个整体.
(3)思想方法上设置的问题是:这节课用了哪些思想方法?学生的回答有:三角学中测量地球周长用了相似三角形法;测量月地距离是将问题情境进行数学抽象,构造直角三角形法得到正弦定理;运用建模的方法研究角的函数;数形结合画出半个周期内的图象;两角差的余弦展开公式既要合理猜想也要严谨论证.
教材中的知识一般以逻辑顺序呈现,但不一定符合学生的心理顺序.学生在初中已学习解直角三角形,在此基础上融入数学史学习解一般三角形,可以帮助学生理解知识产生的必要性,构建知识之谐.通过历史上不同时期数学家们的研究重点,让学生掌握分析三角形边角关系、函数模型研究三角函数的方法,展示方法之美.基于画出函数图象的需要,让学生自主探究解决横、纵坐标问题并探索两角差的余弦公式,引发学生的兴趣和好胜心,在试错中养成一般性思考问题的习惯,营造探究之乐.学生在探究过程中跨越时空与数学家“对话”,感受三角学与天文学的渊源,体现数学的多元文化价值,揭示文化之魅[4].通过引导学生解决历史问题,提升了数学抽象、直观想象、数学建模、逻辑推理等核心素养,实现能力之助.通过走古访今,呈现了数学家们在历史发展过程中的智慧以及认知局限性,帮助学生树立科学可持续的数学观,达成德育之效.
