讲好题目背后的“故事”
2020-12-03广东省深圳市高级中学518040
高 军 (广东省深圳市高级中学 518040)
学习数学意味着解题,解题教学对数学知识的讲授、数学方法的提炼、数学思想的形成有着重要影响.如何挖掘题目的内涵,讲好题目背后的“故事”,对构建学生知识体系、提高学生分析问题和解决问题的能力显得尤为重要.本文结合具体案例及笔者对解题教学的认识,谈谈如何提高解题教学效果.
1 引例
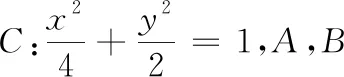
(2)是否存在x轴上的定点Q(异于点A),使得以MP为直径的圆恒过MQ与BP的交点?
分析 定值、定点问题是高考的高频考点之一,也是圆锥曲线学习中的重点和难点.此题以椭圆为载体,在动态情境中同时考查了定值、定点问题,解法多样,思想丰富,内涵深刻.如何讲好此题,最大限度发挥其教学功能与价值,笔者从下面三个方面(“故事”)作了探索.
1.1 “故事1”——试题解法探究
思路1 设而不求,进行整体代换

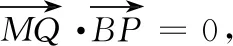
由第(1)问得2x0+my0=4②,将②式代入①式有n(x0-2)=0,x0≠2,解得n=0.因此存在x轴上的定点Q(0,0),使得以MP为直径的圆恒通过MQ与BP的交点.
思路2 联立消元,巧用韦达定理
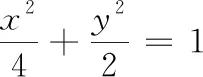
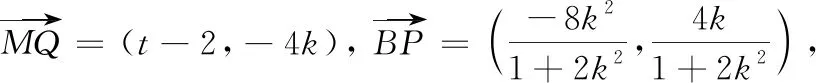
评注试题解法探究展现了解析几何问题解决的两种基本思路,我们简称韦达定理型与非韦达定理型.对于单动点问题(其他所有变量都因某个动点的变化引起的)即非韦达定理型,我们常用设而不求思想,寻找各变量的隐性关系整体代换求解;对于双动点问题(其他变量因直线与曲线两交点同时变化而引起的)即韦达定理型,我们需设直线方程,联立消元后用韦达定理解决问题.
1.2 “故事2”——问题本质探究
题目中的问题是非本质的,由特殊到一般,能否证明下列命题:

(2)是否存在x轴上的定点Q(异于点A),使得以MP为直径的圆恒过MQ与BP的交点?

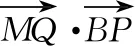
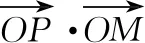
1.3 “故事3”—— 椭圆生成探究
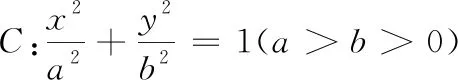
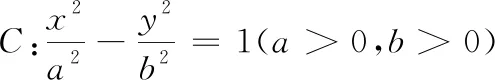
结合上述结论,小试牛刀,解决下列问题:

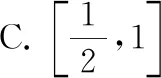
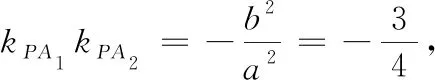
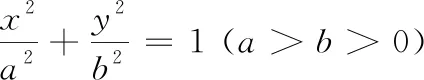
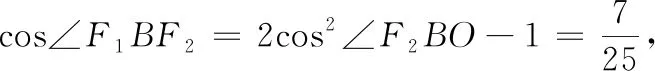
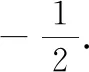
(1)求曲线C的方程,并说明C是什么曲线.
(2)过坐标原点的直线交曲线C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.(ⅰ)证明:△PQG是直角三角形;(ⅱ)求△PQG面积的最大值.
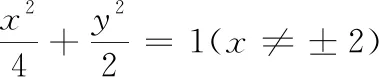
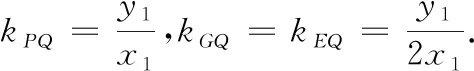
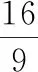
2 思考
2.1 实施多维探究 讲清问题本质
本文对一道高考模拟题从题目解法、问题本质及圆锥曲线的生成等几方面进行了探究,培养学生从多角度自主探究问题的意识,提高学生分析问题和解决问题的能力.数学教育家弗里德曼在《怎样学会解数学题》中写到:把习题看作是精密研究的对象,而把解答习题看作设计和发明的目标.在解题教学中,教师不能就题讲题,停留在问题的表面,而应从多角度分析和研究问题,实施多维探究,讲清数学思维过程和问题本质,让学生经历知识发生、发展及思维过程,形成科学的思维习惯.
2.2 及时总结反思 提升思维能力
数学解题不应仅仅满足于求出答案.当问题还没有解出来时,教育学生能够坚韧不拔、锲而不舍;当答案已经找到时,引导学生应从解题过程中自觉吸取营养,及时进行新的探索和总结反思:解题中用到了哪些知识?它们怎样联系起来?思路是怎样打开的?思维有无多余回路?还有别的解法吗?问题能够推广吗?改变一下条件如何?改变一下结论如何?等等.教师要教会学生提出问题的方法,引领学生学会归纳、整理,将知识和方法条理化、系统化,在及时总结反思中提升思维能力.
