巧用错例 优化教学——错题分析及应用研究

王科峥

一、策略性知识典型错题的原因分析

典型错题是指学生解数学题时，在口答、书面等练习中呈现出的错误率较高的数学题。如果错题的知识属性是属于策略性知识，笔者把这样的错题定义为策略性典型错题。

1.受身心发展制约，未发现新旧情境中的结构性细微差异导致错误。

案例一：我的前面有9 人，后面有5 人，一共有多少人？学生的错误解答：9+15=14，错误率为57.7%。

对学生的访谈：

生：因为是求“一共有多少人？”前面有9 人，后面有5 人，就是9+5=14（人）。

师：你认为这样做对吗？

生：对的呀。

师：前面9 人包括他吗？后面呢？

生：不包括。

师：那说明9+5=14（人）是错的。错在哪里呢？

生：没有把自己加进去。

从访谈中看，对于9+5=14这种解题策略，学生本人还是坚持自己是正确的。说明学生对求“部分数+部分数=总数”这个陈述性知识是掌握的，但为何还错呢？原因在于题中有三个部分数，而“我”这个部分数比其他两个部分数更具有“隐性”因素，学生未能发现“新”的变化。还是坚持用原有的思路：总数=部分数+部分数，这是出错的主因。

2.由于认知结构的缺陷，导致解题策略的错误推广。

案例二：A 盒中有25 个玻璃球，B 盒中的玻璃球个数比A 多15 个，B 盒中的玻璃球个数比C盒多18 个？B 盒中有多少个？C盒中有多少个？学生的错解出现在求C 盒：40+18=58（个），错误率为34.3%。

对学生的访谈：

生：B 盒中的玻璃球个数比A 多。

师：（指着“多”）你是看到多，就想到了什么？

生：加法。

师：老师教你们的时候是这样教的吗？

生：（笑笑）不是，老师说什么大数、小数的。

师：那你为什么不用老师的方法呢？

生：太麻烦了。

分析一个量比另一个量多（少），需要分析出大数、小数、相差数，然后找到相应的数量关系即：大数＝小数＋相差数，小数＝大数－相差数，相差数＝大数－小数。

3.学生对认识和解题中的一些特殊要求存在困难，导致解题策略的错误。

案例三：从一张长36 厘米，宽20 厘米的长方形纸上剪下一个最大的正方形，求剩下部分图形的周长是多少？学生错解如下：

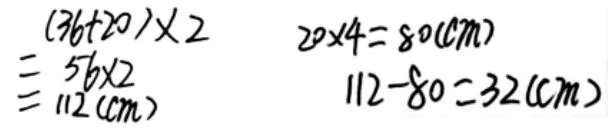
学生访谈：

师：你怎么会这样做?

生：我先算长方形周长，再算正方形周长，最后把两个相减。

师：是吗？你是怎么想到可减的呢？

生：剩下的周长啊。

“求剩下的量，用减法。”这是学生已多次应用，并且验证正确的观念。而由于周长计算具有特殊性即“有限图形周长的不可加（减）性”。对于这个知识的认识，完全颠覆了学生对求“剩下量”的认识。

4.由于概念图式不够丰富，缺乏联系，导致解决应用策略的错误。

案例四：根据图形，画出距离是8 厘米的高。

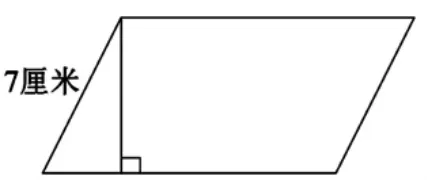
学生访谈：

师：你是怎么想的呢？

生：题目里只说画8 厘米的高，没有说要画在哪条底上，我就按自己的习惯画了这一条。

师：画好后，你想过这条高可能是8 厘米吗？

生：（低头想了好一会儿）不对，应该是斜边长一点。

师：好厉害哦，能够想到这一点。你当时怎么没去想呢？

生：（指了指左边的三角形）我画出来后，就认为对了，再也没去想了。

从学生的访谈中看，解决此题的三个知识点，即直角三角形的斜边大于任何一条直角边、画高的技能、平行四边形有两类高，学生都是明白的。

二、策略性知识典型错题在教学中的应用策略

对于策略性典型错题的教学，如何进行优化？我从以下两个方面入手。其一，铺垫性策略，做好铺垫，预防出错，提高正确率；其二，过程性策略，在教学推进中，找准容易出错的地方，突破难点；其三，练习反思性策略后期跟进，分析错因，纠正错误。

1.铺垫性策略。

有些错误是学生在新知识学习前，由于原有的知识结构“缺陷”、技能缺失等因素引起思考的错误，就要采用提前铺垫，为学生奠定“正确想”的知识技能基础。

（1）加强陈述性知识和程序性知识的教学，夯实“正确想”的知识基础。

在策略性知识的了解阶段,陈述性知识显得尤为重要。在转化阶段, 程序性知识又起到了重要的作用。要注重在操作程序中夯实陈述性知识概念。

如案例二是因为学生原有认知里知识结构出现了错误，即看到“多”就用“加”，看到“少”就用“减”。所以我们应该在新知教学前做好铺垫。

首先建立正确的概念。题中的“多、少”与“加、减”运算没有直接的逻辑推理关系。

本文实验环境为Linux操作系统，搭建了一主四从的小型分布式集群，各节点虚拟机处理器配置为Intel Xeon CPU E5-2650 v2，内存 4GB，软件为Hadoop-2.6.0版本。实验数据采用从UCI机器学习库中选取的美国1990年的人口普查数据，该数据集的维度为68，共有2458285条数据，通过人工处理，将数据集抽样为6个大小不同的数据集，使得每个数据集的数据量以接近2倍大小的速度增长。

其次建立正确的程序。第一步，知道（ ）与（ ）比；第二步，比的结果（ ）多、（ ）少；第三步，求（ ）；第四步，确定解决方法。

（2）加强“数学表示”直观能力培养，奠定“怎么想”的基础。

小学生正处于由形象具体思维向抽象逻辑思维的过渡阶段，在问题解决中思维需要直观的“数学表示”来支撑思考。这种能力要从低年级开始培养。具体有三个方面：首先，培养图示与文字的转化能力；其次，培养“符号”表示的能力；最后，重视图示与条件间匹配的能力。

2.“过程性”干预策略。

所谓“过程性”干预策略，即在新知识学习的发生、发展的过程中，针对新知识的特点，找到学生思维可能出现障碍、阻隔的地方，引入相应的干预策略，突破难点，使学生头脑中构建起“怎么想”的正确思路和方法。

（1）用题组对比显示新旧知识概念差异，减少出错。

新旧知识在概念表述、题型结构、思考方法等具有某种相似性，这种相似性掩盖了其差异，而概念差异可能是学生思维出现阻隔、障碍的“节点”。在教学中破解新旧知识的差异是干预的重点，其最常用策略是题组对比。

如案例三，学生受到原有知识经验的负迁移而出错，可以提供如下题组。

通过对比，凸显题①和题②都表示具体量。通过题②和题③的对比，重点突出③中是“率”。

（2）在解决多个概念融合的综合题时需清晰概念，建立解决程序。

一些策略性典型性错题干预后仍有较高的错误率。这就需要帮助学生清晰概念，建立解题的关键程序。

一个数省略万后面的尾数是8 万，这个数最大是（ ），最小是（ ）。

要解决这个题目需要抓住三个关键：

近似数是一个区间，用数轴的直观形式帮助理解“区间”。

要清晰“最大”和“最小”两个词的含义。

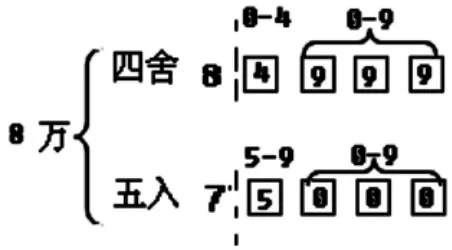
要明确清晰可具体操作的程序，就需要配直观图示（如上图）。首先，要判清楚“舍”与“进”的数位；其次，根据四舍五入中最大与最小排列出数字；最后，按照题目要求找到最大和最小的数。

3.错误产生后的纠错策略。

（1）发现错因策略。

策略性典型错题的错因与陈述性、程序性知识属性错题的错因相比，更为复杂、更为隐性。需要关注两点：第一，原来是怎么想的？第二，错在哪儿？

通过“说”、“写”等方式，认识“原来是怎么想的”。

通过正确与错误的方法对比，认识“错在哪儿”。

错误思维方式往往带有一定的隐蔽性和顽固性，仅靠教师的正面示范，让学生认识错误，改变原来的思维方法，效果会比较差。

（2）矫正错误策略。

矫正错误更重要的是矫正错误的思考方式和思考方法，仅仅靠一个错误题目的订正难以实现，需要在多种变式练习中完成。提供非概念变式练习题，凸显出变中的不变，及时巩固正确的想法。还可以提供概念变式练习题，在这些变式题的练习中，凸显出变与不变的应对方式，达到融会贯通。

提供非概念变式题，及时巩固。

提供相同类型的习题，让学生在解决这些习题中不断强化正确的思考方式，以此弱化原有的思考方法。在这个过程中，不是以正确的解答为主要目的，而是要以改变思考方法为主，让学生通过写、画、说等多种不同的方式来表达正确的思考方法。要增加与原题目的对比，凸显出不变的方法。

提供概念变式题，融会贯通。

提供变式习题，既能巩固原有正确的思考方法，又能达到举一反三、触类旁通的作用。在这个过程中也要与原题进行对比，凸显出变化的地方及改变相应的思考方法。