数缺形时少直观 形少数时难入微——《数与形》教学实践与思考

王陈亮

【教材与学情分析】

数形结合思想是一种非常重要的数学思想，涉及到数学学习的各个领域。我国著名数学家华罗庚先生曾说：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休。”数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”等抽象思维与形象思维的结合，使复杂问题简单化，抽象问题形象化。

《数与形》是人教版六年级上册“数学广角”中的内容。本课旨在让学生通过自主探究图形中隐藏着的数的规律，尝试应用所发现的规律解决问题，感悟数与形的广泛联系，同时在利用数形结合解决问题的过程中感悟数形结合的数学思想。

【教学过程】

一、前测导入，梳理回顾

师：同学们，“数与形”一直伴随着我们的数学学习，课前，我们进行了回顾与整理，下面请大家一起来欣赏同学们的作品。

课件依次出示：

出示图1：

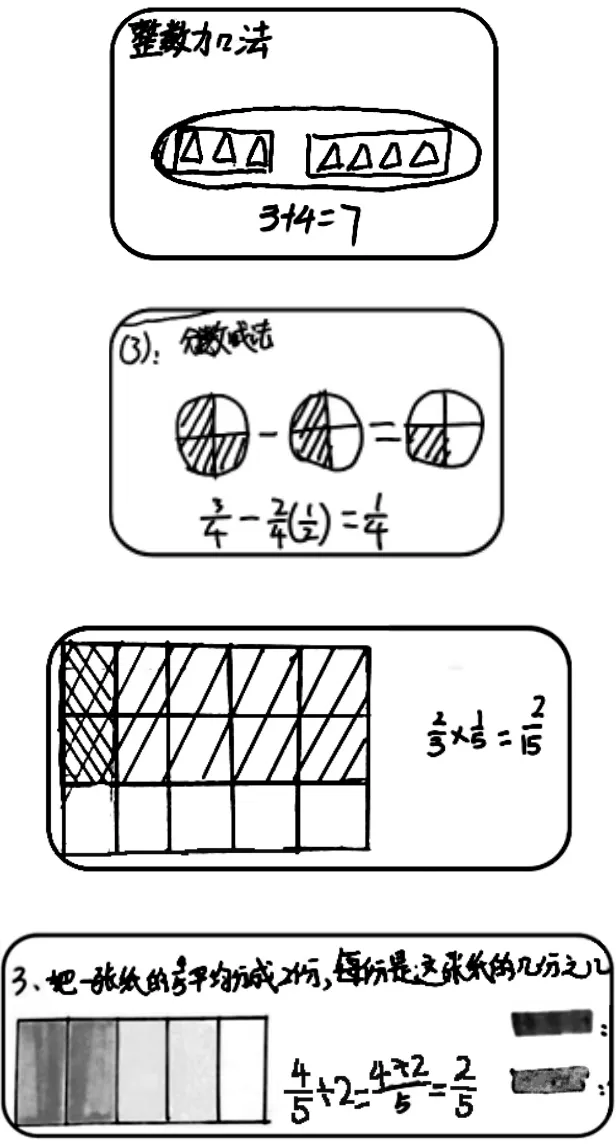
师：从作品中哪里看到了数与形？

生：在加减计算中，往往用图来解释计算的算理。

出示图2：

师：你看到数与形了吗？

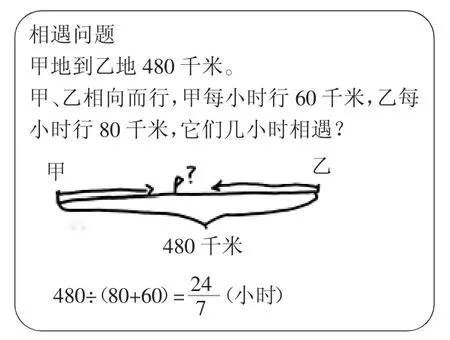
生：用线段图帮助解决行程问题。

出示图3：

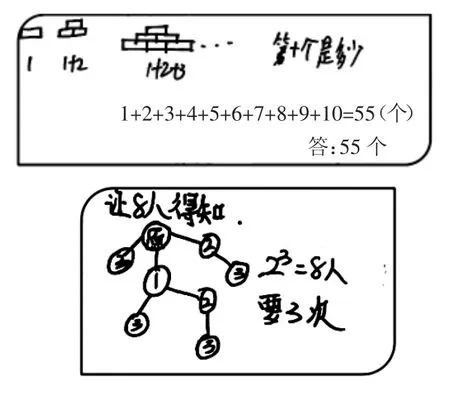
师：这里又用到了哪些数与形？

生1：用数字或者算式表示图形的规律。

生2：还可以用图形表示打电话问题中所用时间的规律。

师：在前面所学习的计算、解决问题、探索规律等问题中，有时用图形表示数的规律，有时用数描述图形的规律。今天这节课我们将继续研究“数与形”。

【设计思考：学生对于“数与形”的知识有着零散的学习经验，这些经验又是学习本课知识的重要经验基础。在课前安排前测整理学过的“数与形”的知识，教学中基于学生已有的经验，通过呈现学生的前测材料，并且分类呈现，更有利于学生从整体上回顾“数与形”的知识，也有利于学生对本课知识的学习。】

二、活动推进，探究新知

1.设置悬念，激发探究。

（课件依次出示零散1 个、3个、5 个、7 个小正方形）

师：如果继续出示，你猜我会出示几个小正方形？

生：9 个。

师：刚才一共出示了几个小正方形？

引出算式：1+3+5+7=16。

出示小精灵的对话：还可以用4×4 或42表示。

师：你知道是为什么吗？

2.活动一：沟通算式和图形之间的关系。

活动一：

请你在方格中画图表示加法算式，又能用42表示。

（1）用彩笔在方格图上画图表示。

（2）典型展示。

活动一：“1+3+5+7”与“42”

请你在下面的方格中画图表示上面的算式，又能用42表示。

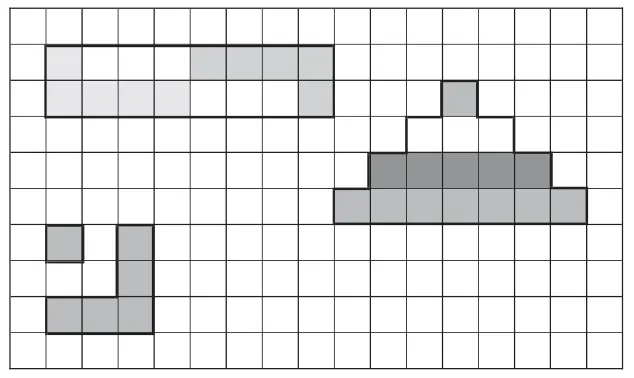
师：这几种画法各有什么优点？你更欣赏哪一种？

生1：我欣赏第2 种，很容易看出依次增加2 个。

生2：我最喜欢第3 种。既能清楚地看出1+3+5+7 个图形，还能清楚地看出4×4 或者42。

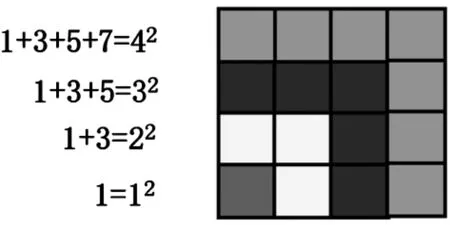
3.研究数和形的规律。

（请学生板演用小正方形摆一摆。进一步沟通数和形之间的关系）

师：如果一层一层往里剥，又能得到哪些正方形？算式如何表示？（借助课件依次出示）

师：观察下面图中的数和形，你有什么发现？

生1：加数越来越多，正方形也越来越大。

生2：有几个加数，和就是几的平方。

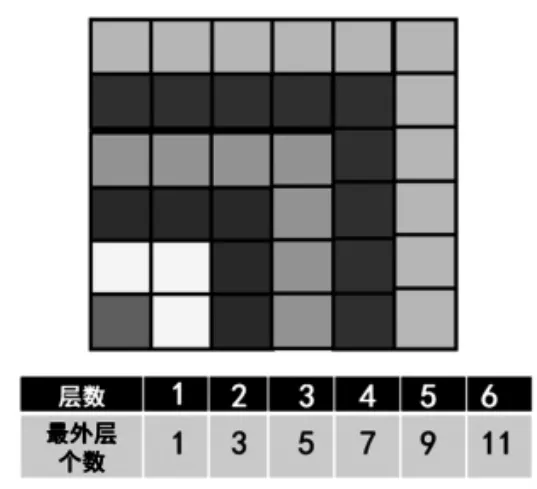
师：如果继续一层一层地往外包，又会得到哪些正方形？你能想象出来吗？

思考：如果再包两层，最外层有几个正方形？

生：按照顺序思考。

师：有没有不一样的思考？

（引导学生从层数与个数的角度思考，结合统计表进行研究）

4.活动二：层数、最外层个数和总数之间的关系。

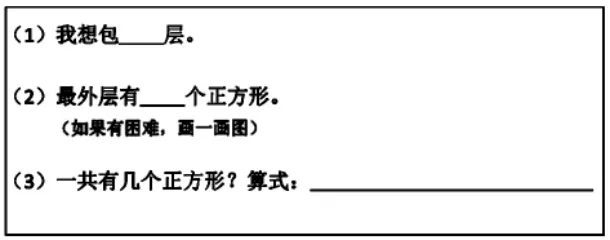
交流展示：

依次展示3 份不同层次的作业。

我想包10 层。……

我想包100 层。……

我想包n 层。

师：用算式如何表示呢？

吃过早饭，我就去看二丫，给她带了碗锅巴粥。一进门，金宝就把我拉到一边，红着眼睛说：“已经水米不进了。”

生：如果是包n 层，最外层是2n-1 个正方形。算式是：1+3+5+7+9+……+（2n-1）=n2。

【设计思考：在数与形的新知探究环节如何设计上，我预设过几种不同的方式，比如出示几个不同个数小正方形拼成的大正方形，让学生用数表示，或是出示等差数列的连加算式，让学生用形去表示，效果都不甚理想，最后在专家的指导下，采取了用悬念引入的方式，激发学生探究的欲望。新知的展开上，通过预设两个大活动，让学生在活动中去探究、去交流、去分享，再引导梳理，既沟通了数和形之间的关系，同时又基于形的研究拓展了学生的数学思维，效果较好。】

三、分层练习，拓展思维

1.变式练习。

学生独立练习，校对反馈。

2.发散练习。

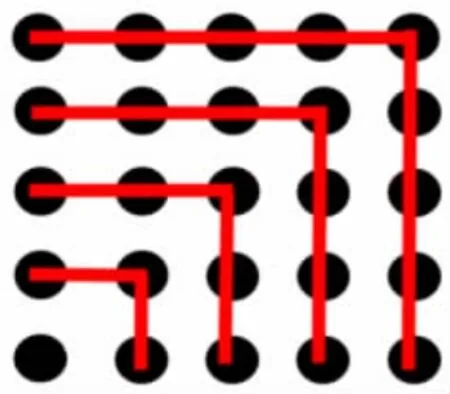
出示5×5 个小圆点。

师：今天我们从这样的角度构造，得到了25=1+3+5+7+9 的算式。

师：还能设计其他构造，用不同的式子表示吗？

经过交流，选择出正确的算式。

接着教师引导学生进一步思考：剩下的3 道算式该用怎样的形去表示呢？

继续引导思考：

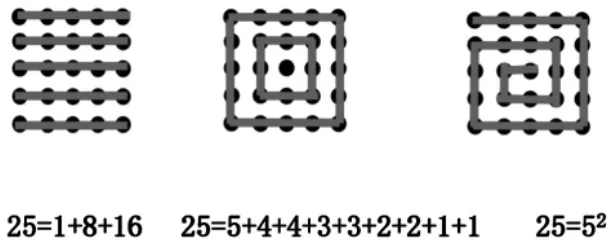
（结合学生的交流，逐步揭示答案）

3.认识“形数”。

师：上面认识的这些数都是正方形数。

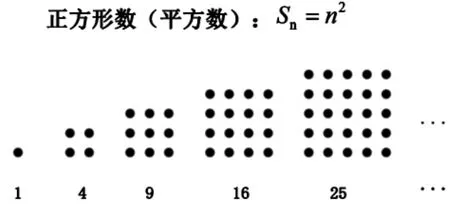
4.拓展认识。

三角形数、五边形数、八边形数、四面体数。

介绍毕达哥拉斯的“形数”。

【设计思考：本课的练习体现了层次性，从基本练习到开放练习，再到拓展练习，满足不同学生的学习需求。同时体现了练习的整合性，一个5×5 的正方形图，从不同角度进行挖掘，让学生感受数学的美。教学中在充分认识正方形数后，接着又让学生认识了三角形数、五边形数……充分展示了数学的美感。】

四、课堂小结，畅谈体会

出示华罗庚关于“数与形”的名言（略）。

师：请结合这节课的学习，谈谈你的感受。

生：数用形表示会更加直观，形用数去描述会更加入微。

生：利用好数与形的知识，可以更好地帮助我们解决生活中的数学问题。

师：（小结）希望同学们今后碰到一个问题时，能从数和形的角度一起思考。

【设计思考：在课的最后出示我国著名数学家华罗庚的名言，让学生畅谈收获和感受。由于有了前面的学习和交流，当问学生在读了这首小诗后有什么感受时，学生话匣子打开了，侃侃而谈，表达得非常精彩！】

【教学反思】

一、前测——为教学导航

《数与形》一课是人教版教材六年级上册“数学广角”中的内容，虽然是一节新课的教学内容，但是却一直伴随在学生的数学学习中。在本课教学前，安排了一个前测整理的活动，让每位学生回忆自己在之前的数学学习中有关“数与形”的知识。有了课前的整理复习，为学生后续新课的学习做好了铺垫，因此，在本节课的教学就基于学生的前测展开，从课堂的教学效果来看是非常好的。

二、活动——助推教学深入

本节课的教学，基于学习活动展开学生的数学学习，在一节课中努力设置两到三个大活动，让学生在这样的大活动中理解数学知识，突出重点，突破难点。比如在课的一开始通过连续出示小正方形，得到算式：1+3+5+7=16，还可以写成4×4 或者42，你知道这究竟是为何吗？引导学生深入思考，同时提供《学习单》让学生去表示，从而让学生自主探索，弄清数和形之间的关系。再比如借助正方形的研究得出几个数和正方形的关系后，引导学生继续深入思考，你还想包几层？最外层有几个正方形，一共有几个正方形？让学生在活动中探究规律。现在的课堂趋势是提倡大活动、大问题，一节课精心预设几个大问题，避免琐碎的乒乓式的交流，这样也使学生的讨论学习更加充分。

三、数与形——拓展学生数学思维

本课的主题就是“数与形”，基于数与形之间的关系，引导学生进行数学思考。比如，这样的形可以用什么数表示？这样的算式又会是哪一个形呢？在这些各种关系的探索中，引导学生的数学思维不断深入。比如，在探索了5×5 正方形和算式之间的关系之后，如果再包两层是怎样的正方形？最外层有几个正方形？一共有几个正方形？让学生结合形去思考数和形之间的规律。再比如在5×5 的小圆圈点阵图中，不同的构造可以表示成不同的加法算式，接着继续引导学生思考，如果不同的构造，可以表示出哪些形，哪些数和形是相对的等等，在数和形关系的不断交流中，将学生的思考引向深入。