由简及繁，促进思维发展——《圆的周长练习课》教学设计

陈林秀

【教学内容】

人教版六年级上册第65、66页。

【教学过程】

一、创设情境，由最美的平面图形说起

谈话引入：圆是世界上最美丽的平面图形。圆因为其独特的特性被广泛地应用于我们的生产和生活中。它的周长中会不会也隐藏很多奥秘呢？这节课，我们就来探究神秘的“魔圆的周长”。

【设计意图：通过设置悬念，由神秘的魔圆切入，引发学生的好奇心，激发学生探究的欲望。】

二、思维之旅，从引导探索开始

●活动一：魔圆初现，初解圆的周长。

1.提出问题。

课件出示两个圆。

师：要求这两个圆的周长，需要哪些条件？（半径或直径）

师：告诉你其中一个圆的半径和另一个圆的直径，请分别求出它们的周长。

（学生独立思考并计算，汇报交流）

（教师板书：c=πd、c=2πr）

2.小结提升。

师：这两个周长公式我们可以把它看成一个公式。知道为什么吗？

预设：c=2πr 这个公式中2r=d，所以，我们只需记忆并理解c=πd 这个公式就可以了。

【设计意图：通过计算两个圆的周长，唤起学生已有的知识经验，利用公式求周长，再次沟通两个圆的周长公式之间的关系，有利于学生理解记忆并运用周长公式。】

●活动二：魔圆大变身，初探半圆的周长。

1.提出问题。

师：如果我将其大圆沿着直径切掉一半，剩下部分是什么？

预设：半圆。

师：猜猜看，这个半圆的周长是多少？

（学生活动：学生猜测，汇报交流想法）

预设1：半圆的周长是12.56÷2=6.28（cm）。

预设2：半圆的周长包括一条曲线和一条直径，曲线的长度是圆周长的一半，所以应该是6.28+4=10.28（cm）。

师：你们认同哪位同学的想法？为什么？

（学生活动：观察分析，对比思考，汇报交流）

预设：半圆的周长不仅包括圆周长的一半还包括一条直径。

（教师板书：半圆的周长=圆周长的一半+一条直径）

2.变式练习。

课件出示：

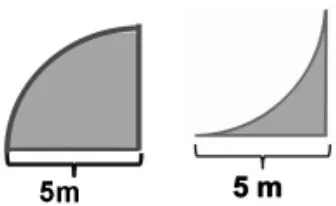
师：这两个图形哪个面积比较大？（第一个）

师：（追问）不计算，你能知道哪个周长比较长吗？

（1）学生活动。

（2）汇报，全班交流。

预设：两个图形的周长一样。两个图形的周长都是两条5m 长的线段再加上圆周长的。

（课件演示，验证结果）

【设计意图：通过猜测半圆的周长，启发学生思考明辨“半圆的周长”与“圆周长的一半”的区别与联系。让学生在思辨的过程中加深对周长概念的理解，并能灵活地应用周长公式解决问题。】

●活动三：半圆大变身，探索曲线的奥秘。

1.提出问题。

师：我们的半圆摇身一变，变成了下面的样子。猜猜看，上面的线和下面的线哪条长一点？

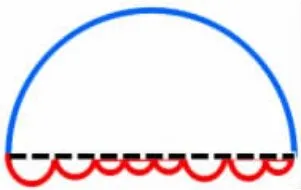
预设1：上面的线长一点。

预设2：可能一样长。

师：怎样才能确定到底是哪条长呢？

预设1：分别算出长度，比一比。

预设2：要算下面的长度太麻烦了，我们可以用化繁为简的方法，先研究半圆数量少一点的两条线之间的关系。

2.深入研究。

师：那我们就从研究简单的有两个小圆的组合图形入手。

师：如果把这两个圆像下面这样拼在一起，这个图形的周长是多少？

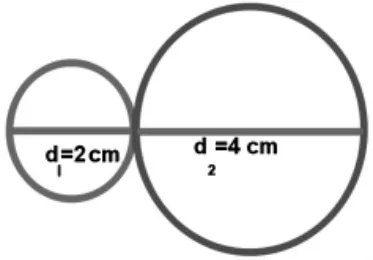
预设：把两个圆的周长加起来，18.84cm。

师：想象一下再在外面画一个大一点的圆，会是什么样子?

（1）学生活动：想象。

课件出示图片：

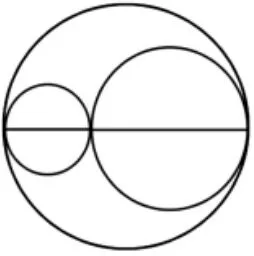
师：大圆的周长和两个小圆的周长之和比较，谁长？

（2）学生活动：思考、计算，汇报交流。

预设：大圆的周长是18.84cm，正好是两个小圆周长之和。

师：现在把里面的圆变一变，变成三个圆，谁长？

（3）学生活动：思考、计算，汇报交流。

预设：一样长。

师：里面的圆再变一变，变成四个圆呢？

预设：还是一样长。

师：你发现了什么？

预设：大圆的周长正好是里面小圆的周长之和。

师：为什么呢？

预设：圆的周长=圆周率×直径，四个小圆的直径之和正好是大圆的直径。所以，大圆的周长正好是四个小圆的周长之和。

（课件演示验证）

小结：不管多少个圆，只要小圆的直径之和等于大圆的直径，那么大圆的周长就是这几个小圆的周长之和。

3.应用规律。

（1）课件出示：

师：上面的线和下面的线哪个长？为什么？

（2）课件出示：

师：请比较，这两个阴影部分的面积谁大？

师：这两个阴影部分的周长谁长？你是怎么想的？

【设计意图：通过设置问题情境，激发学生探究的欲望。让学生经历观察、猜测、验证、发现的研究过程，既培养了学生科学、严谨的学习态度，对策略意识也有了更加深入的认识。】

●活动四：捆绑魔圆，拓展应用

1.提出问题。

师：超市把6 瓶底面直径为8cm 的罐装饮料捆在一起销售，你们能想出哪些捆绑的方法？选用哪种捆绑方法更节省胶带？

（1）学生活动：分组活动，动手研究。

师：可以先画出草图表示你的想法，再在小组内部交流。

（2）在《练习单》上画一画，算一算，填一填（略）。

（3）展示交流。

学生展示自己画的草图，交流想法，汇报计算方法和结果。

（4）组织学生比较。

汇报预测：

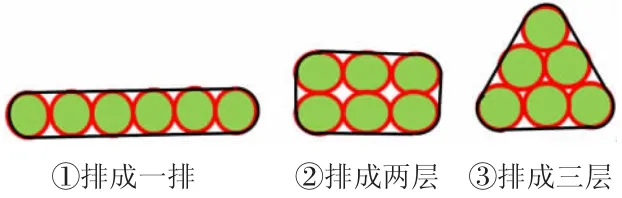
最优方案预测：当圆与圆中间部分周长最大时，所用的胶带最少。

数学思考：方案②和方案③，所用胶带都一样，为什么在超市中我们基本上看不到方案③这种绑法呢？

方案②不仅用得胶带最少，在装箱的时候更节省空间。

【设计意图：让学生对优化策略有了更加全面和深入的认识。同时进一步体会到数学来源于生活又应用于生活。】

三、回顾总结，提出问题

师：今天的学习你有什么收获？

师：解决问题的过程中有什么心得？

师：还想到了什么新问题？

【设计意图：通过回顾梳理，总结反思，让学生对圆的周长有了总体的认知，培养其探究意识和问题意识，增强解决问题的能力。】