『变』中求『同』 『进』中寻『根』——以《20以内进位加法》单元整理课为例

郑志霞

【教学内容】

人教版一年级上册第88、89页。

【教学过程】

环节一：知识回顾，整理分类。

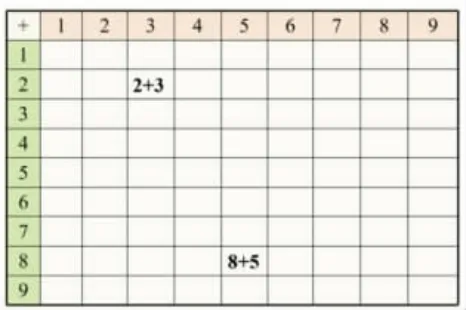
师：我们已经学习了20 以内的进位加法，仔细观察这张表格，空格中该填哪些算式？

（课件把表格补充完整）

师：找一找，哪些是进位加法，哪些是不进位加法？

生：1+9、2+8、3+7、4+6……8+2、9+1，这些算式得数刚好是10，所以这些都是进位加法，而左边的都是不进位加法。

环节二：理解算理，求联求同。

1.布置任务：这些进位加法都是怎么算的？选择其中一个算式说一说、写一写、画一画。

2.反馈。

（1）以9+4 为例，说说你的想法。

生：9+4=13，可以从4 里面拆出1，和9 凑成10，10 再加上3等于13。

生：如果摆小棒的话，它是把9 根和1 根合起来，变成一捆，然后再加上3 根，所以等于13 根。

生：也可以借助计数器，先拨9 颗珠子，再拨4 颗，个位上满十进一，先在十位上拨1 颗，再从个位上拨走10 颗，所以等于13。

师：这三位同学的方法有什么相同的地方？

生：其实都是从4 里面拆出1，和9 凑成10，再计算。

生：都是用“凑十法”计算的。

（2）延伸到“9 加几”。

师：那这一行的其他算式又是怎么算的呢？（9 加几的算式：9+2、9+3、……9+9）

（学生陈述略）

（3）求同，提炼“凑十法”模型。

师：刚才在拆数的时候，有什么相同的地方？

生：都是拆出1。

师：这是为什么呢？

生：前一个加数都是9，那么我们可以从另一个加数中拆出1，和9 凑成10，再计算。

师：如果是8+几、7+几、6+几，那应该怎么算？

生：拆出2，和8 凑成10；拆出3，和7 凑成10；拆出4，和6凑成10。

师：拆出来的数在变，这是为什么？

生：后面拆出几，要看前面那个数是几，只要它们相加等于10就行了。

（4）“凑十法”再应用。

师：这一列算式该怎么算呢？（出示算式：7+4、8+4、9+4）先自己说一说。

生：7+4，把4 分成3 和1，7+3=10，10+1=11。

生：8+4，把4 分成2 和2，8+2=10，10+2=12。

生：9+4，把4 分成1 和3，9+1=10，10+3=13。

师：这里都有加4，为什么拆法不一样？

生：前面的加数是7，加上3才等于10，8 的话就应该加上2，9 应该加上1。

师：也就是说，前面比较大的加数不同，后面4 的拆法也不一样，但都是先凑十再计算的。

环节三：习题练习，巩固提高。

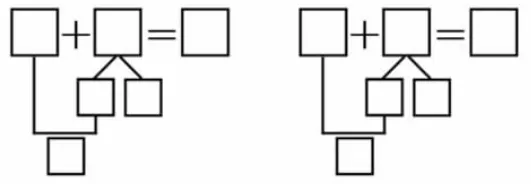
1.写一写，比比谁写得多。

2.挑战一下：37＋5。

师：你是怎么算的？

生：把5 分成3 和2，37 和3相加等于40，再加2 等于32。