对“10”的再认识

王张妮

在众多研究中可以发现这样的趋势：随着家庭教育与学前教育的普及与规范化，儿童的认知起点越来越高。学生常常是带着一定的知识进入课堂，在学习《认识10》这一课之前，多数学生已经会认读10，理解10 所表示的具体数量，能基本区分基数10与序数10，还能进行10 的合成与分解。这使我们不得不思考：在这些基础之上，“认识10”究竟还要认识些什么？如何展开教学以促进学生在更深刻的水平上理解10 的概念呢？

一、两个重要的“第一次”

“10”这个概念出现时，学生将会遇到两个重要的“第一次”：第一次出现新的“计数单位”——此前学生已知的计数单位是1；第一次出现“位值”的概念，作为第一个被认识的两位数，10 引出了新的“数位”，每个数位又都有特定的“位值”。毫无疑问，两个重要的“第一次”，使10 变得与前面学习的自然数有所不同，所以10 的计数法意义才是教学真正的重点。但，数位和计数单位这样的概念十分抽象，如何在学生现有的认知水平中自然渗透，把两个“第一次”教清楚、让学生学明白就成了教学的难点。

1.第一次出现新的“计数单位”。

10 不仅可以表示1 个集合中的十个元素，还可以表示10 个元素组成的一整个集合，即“10 个一”就是“一个十”。事实上，任何数都存在这样的双重属性，既是一个集合中的若干个元素，又是若干个元素组成的一个集合，但由于人类在探索和计数的过程当中，将十进制作为最主流的计数方法，于是产生了10 这个重要的“计数单位”。

学习一位自然数时已经学过自然数的计数规则是“+1”的逐一计数法，那么10 就是由9 个一再添1个一得到，10 就是10 个一，完成了这一步，可以理解为学生进行了类比迁移，理解了“元素10”。第二步，由10 个元素聚合成为一个整体，构成了“集合10”。反复对“元素10”和“集合10”进行相互转化，理解“10 个一”和“1 个十”是相等的，对于10 这个新的计数单位的理解有着重要的意义。

有了这个概念基础，学生可以迅速突破计数容量，以十为单位进行逐一累加，轻松突破1 个十是10、2 个十是20、3 个十是30……几个十是几十，也为100、1000 等新的“计数单位”的学习埋下认知伏笔。

2.第一次出现“位值”概念。

10 是学生认数过程中遇到的第一个两位数，由“1”和“0”两个已经学过的数字“拼组”而成。如何实现用“1”和“0”表示10？仅靠增加新的“数位”还不够，支撑这一表示方式的重要原则是“位值原则”，不同的“数位”有不同的“位值”，十位上的1 表示1 个十，个位上的1 表示1 个一。“位值”的出现，使得“用有限的数字表示无限的数”变成了可能，这在数学上是一个重要的思想方法。

在10 这个数上，学生可以体验“计数单位”和“位值原则”高度统一，学生头脑中将逐步形成“满十进一”“以一当十”的表象，为计算算理的理解与应用夯实基础。

既然10 的概念如此重要，教学中如何促进学生在更深刻的水平上理解10 的概念？

二、从“生活化”到“数学化”

1.数学情境“生活化”。

10 是学生生活中常常会接触到的数，借助生活化的数学情境可以自然而然地展开对10 的讨论。

●环节1：在关系中引入10。

通过几组关系的比较，让学生理解10 的产生过程是9 添1，从而揭示9 的后继数是10，10 比9 多1；渗透“1+2+3+4=10”的组块关系，探索10 这个数量与其他数量之间的联系。像这样对生活中的数量关系进行观察和比较，帮助学生直观理解“元素10”的含义。

师：讲台上有一些书，一起数一数。（又拿出一本）老师漏放了一本，现在有几本呢？

师：（出示如图叠放的9 块小立方体）有一些小方块，你能快速知道一共有几块吗？如果再添一块呢？观察10 块小方块的叠放方式，你有什么发现？

（引导学生发现叠放方式是从上往下，每一层的块数分别是1、2、3、4）

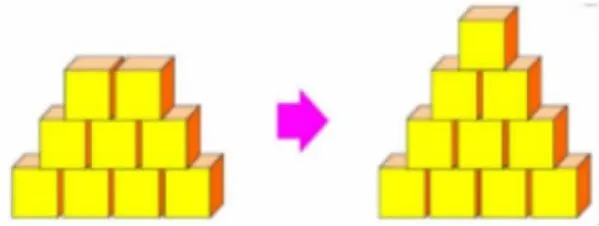
师：同学们已经发现了吧，今天我们要认识一个新的数——“10”（板书10）。通过刚才的学习，关于10，你有什么想说的？

预设：9 添1 是10；10 是比9 多1 的数；1、2、3、4 块小方块合起来是10 块；10 可以表示10 本书，也可以表示10 块小方块，所有10 个物体都可以用10这个数表示……

师：生活中，你还发现有哪些10 吗？

预设：10 个小朋友；钟面上的10；10 路公交车；10 号门牌……

师：原来生活中有那么多10。

●环节2：在操作中理解“10 个一”是“1 个十”。

借助多种学习材料，反复把10 个的东西“打包”成1 个，以熟悉的操作情境帮助学生理解“集合10”。

师：（把10 本书捆成一捆）想一想，把10 本书捆一捆有什么好处吗？

预设：下次用起来比较方便；不用数也知道这里有10 本……

师：没错，把这些书捆成一捆后就知道这里有10 本了。现在老师为大家准备了很多小物品，你来选择一种物品，像老师这样整理吧。

（分组对不同的物品进行打包）

师：（出示一捆书，示范）10 本捆1 捆，1 捆有10本。你能像老师这样汇报你的成果吗？

生：（10 块小方块）10 块装1 盒，1 盒有10 块。

生：（10 支铅笔）10 支扎1 捆，1 捆有10 支。

生：（10 个回形针）10 个串1 串，1 串有10 个。

……

师：你们描述得真准确，不仅用了扎、捆、串等词语，还把数量说清楚了。谁能说一说，听完大家的描述你发现了什么规律？

预设：把10 个东西，打包成了1 份。

师：把10 个一，打包成1 个十。这样我们就知道10 个一组成了1 个十，1 个十里面有10 个一。

2.生活经验“数学化”。

有了上一环节的活动经验，学生初步形成了“10个一就是1 个十”的表象，但是如何将它进一步抽象为一种数学化的表达形式？我们可以把“数学化”理解为对概念原型的反思和概括。只有经历充分具体的过程，才能将其内化、提炼成为自己的知识。

●环节3：用计数单位、算盘等半抽象的认知工具探索10。

利用计数器和算盘等工具再现“满十进一”“以一当十”的过程，帮助理解“十位”的意义。可以重现上几个环节的问题，“在个位上拨9 颗表示9，怎么在计数器上表示比9 大1 的数？”经过尝试与交流，学生有可能联系上一环节的操作经验，创造出在“十位”拨1 颗表示10 这样的方法，教师则可顺势在“满十进一”“以一当十”的尝试中自然引出“数位”的意义。如果借用算盘，更妙的地方在于，学生曾经有“以一当五”的经验，创造出“以一当十”的方法则有更大的可能性。

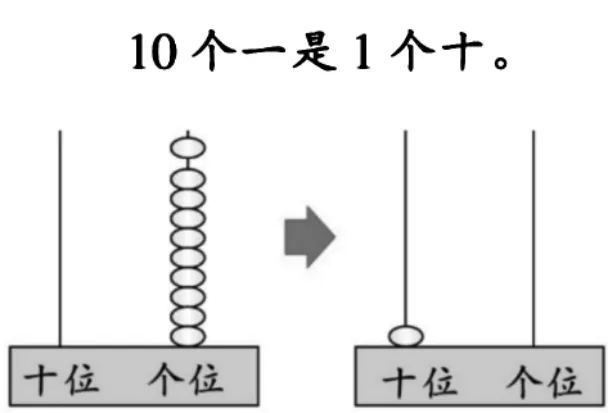
师：我们已经会用计数器表示数，回顾一下怎么表示9？

生：拨9 颗珠子就表示9。

师：（规范语言）1 颗珠子表示1 个一，9 颗珠子表示9 个一，在个位上拨9 颗珠子代表9。今天学习了10，你能用计数器表示吗？请你试一试。

预设：

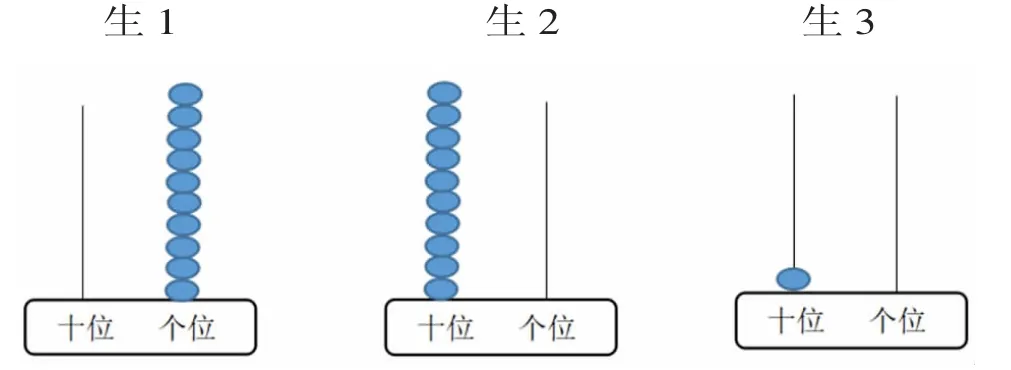
师：说说喜欢的方法，并说一说理由。

由学生自主讨论三种方法，重点讨论第三种方法，并根据十位上1 颗珠子表示1 个十，得出“1 个十也就是10 个一”的结论。

●环节4：在类比迁移中理解10 作为新的“计数单位”。

与“几个一是几”类比，渗透“几个十是几十”的初步认知。

师：（PPT 中1 捆1 捆出示书）书店老板也像我们这样把书捆起来，现在你知道他的仓库里有几本数学书吗？你有什么好方法能够快速知道呢？

预设：10 本10 本数。1 个十、2 个十、3 个十……9 个十。个别学生说出几十。

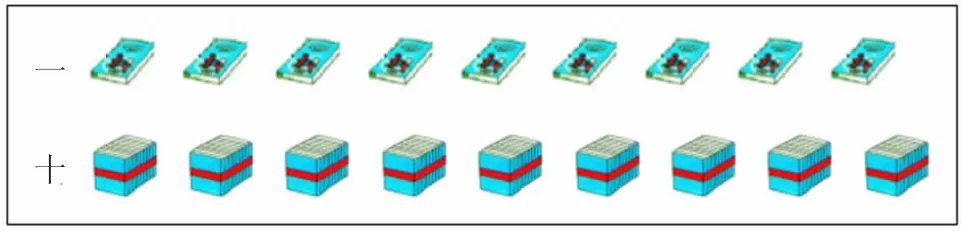
总结：（出示如图两组对比图）第一排一本一本数，1 个一是1、2 个一是2……9 个一是9。第二排十个十个数，1 个十是10，猜一猜，2 个十是——20，3个十是——30……9 个十是90。这是我们以后会进一步学习的。

三、总结

认识10 并不是简单的对“理解10 所表示的具体数量、基数10 与序数10、10 的分与合”等学生已知的事实性知识进行重复机械的再读、再认，而应基于10在课程前后的重要属性，结合学生的认知基础，明确教学目标，厘清重难点，并制定有效的教学策略。

本研究第一个部分中，我们剖析了10 概念的重要性，提出《认识10》这一课的教学重难点为攻克两个重要的“第一次”：第一次遇到新的“计数单位”和第一次建立“位值”概念。

在教学策略中则提倡，要将数学情境“生活化”，形成“以一当十”的表象，在生活情境的支持下，理解“10 个一就是1 个十”，理解10 不仅有10个元素的概念，“打包”后还有1 个集合的概念；又提出将生活经验“数学化”，借助半抽象化的认知工具，凸显“数位”和“位值”的含义，体验作为计数单位的10。