重历算法形成过程,寻求对算理的深度理解
2020-12-02管小冬
管小冬
教完“两、三位数除以两位数”后,我都会给学生们再上节“特殊”的复习课。课上,既没有单元学习的回顾与梳理,也没有日常复习课的对比练习、查错、析错,而是让学生们“忘记”已学的除法计算法则,从头学起,重历除法竖式算法的形成过程,在其间达成对除法的深度理解,感悟这看似寻常的除法竖式中所蕴含的治学方法与精神。
【案例】复习课《我真的懂除法吗?》教学片断
播放视频:记者街头采访一位外国朋友,请他计算8×7。外国朋友知道8×7 就是把7 个8 相加,于是便从8、16、24、32 一直往后加,可惜加到7 个8 时出现了错误,得到答案55。
(观看过程中,很多学生都忍不住笑了起来。随后,教师组织学生交流自己的感受。略)
师:如果请这位外国朋友去算我们刚学过的“两、三位数除以两位数”,比如“823÷21”,想想,他会怎么算?
生:估计会用823 不断去减21,看要减多少次,最后还余多少。
生:也可能不断加21,看多少个21 最接近823。
师:看来大家都认为这位外国朋友知道“823÷21”就是要算823 里有多少个21。不过,如果这么算的话,你们觉得他……
生:(笑着说)他会崩溃的。这也太麻烦了!
师:是啊,根据除法的意义可以得到上面这两种基本方法。但如果每次都这么算,显然太烦了!怎样可以简便?大家有什么适用于他的好建议吗?
生:我觉得他可以先减210。因为虽然他乘法计算能力不强,但21×10=210 还是好算的。
师:那我们就用210 来试试。
师生交流后,教师板书:823-210-210-210=193。
师:接下去怎么办?
生:再用193 去减21,看能减多少次。
师:减多少次,大家知道吗?
生:193÷21=9……4,要减9次,还余4。
(板书:193-21-21……-21=4)
师:最后答案是多少?
生:39 余4。上面减了30 个21,下面还有9 个,一共就是39个,还余4。
师:哎呀,真不简单!在大家的帮助下,这回确实简便了不少。如果他想把除法计算的本领再提高些,有什么好建议吗?
生:那他就得去学除法竖式。
生:学除法竖式前,还得先背乘法口诀表。因为除法竖式计算离不开乘法。
师:(出示823÷21 的除法竖式,如下图)这是我们熟悉的除法竖式,与刚才的计算过程相比,有联系吗?
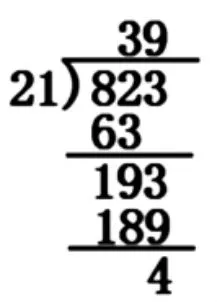
生:除法竖式是把刚才相同的步骤合在了一起。比如,第一步其实就是减去了30 个21,第二步再减去9 个21。
师:大家看出来了吗?除法竖式就是把原来分步减的过程又进行了优化。这样我们计算除法时就方便多了。不过,这么便捷易用的除法竖式,究竟是怎么来的呢?想知道吗?
教师逐步呈现历史上不同阶段的除法竖式。(如下图)

学生阅读后交流自己的理解与感受。感悟除法竖式计算就是一个在反复尝试、调整中,不断逼近、寻找结果的过程。今天所用的除法竖式算法,是一代代数学人不断思考、优化后的智慧结晶。
【思考】重历,为了寻找遗失的美好!
可能会有教师要问,学完“两、三位数除以两位数”后,学生已经基本掌握了除法竖式的算理与算法,为何还要专门花一节课的时间来让学生重历算法形成过程呢?以下是我一段时间以来在除法教学过程中的一些自我追问与反思,这节复习课正是在此基础上生成的。
一、对“除法教学”的追问
除法是四则运算中公认最难的一种运算。一方面,除法竖式的书写形式与学生经验系统中加、减、乘的竖式计算形式不同,因而学生在学习除法竖式时,前序知识带来的负迁移使其需要花费更多时间与精力去理解、掌握;另一方面,除法计算其实是一个逐次乘、减的过程。特别是当除数是两位数及以上时,要顺利且较为熟练地完成计算,对学生在口算、估算、判断、决策、短时记忆等方面均有不低的要求。
为了让学生理解除法竖式的算理,掌握算法,各版本教材多按照“表内除法——有余数除法——除数是一位数——除数是两位数”的脉络进行编排,于螺旋上升中逐步培养学生的运算技能,发展运算能力。在上述各章节内容的具体编排时,编写组专家也是精心设计、煞费苦心。以苏教版《两、三位数除以两位数》单元为例,依次就有“除数是整十数商是一位数的除法口算和笔算”“除数是整数十数商是两位数的笔算”“把除数看作与它接近的整十数试商”“四舍调商”“五入调商”等内容。然而,即使是在这样精细、周密的安排下,学生在除法计算中仍然会出现各种形式的错误。经过教师精心设计的练习与巩固,情况虽然开始逐渐好转,但当五年级继续学习小数除法时,之前我们熟悉的那些整数除法中的典型错误又卷土重来。
由此,我们是否应该做出类似这样的追问:“在整数除法的教学中,我们缺失了什么?”“学生真的懂除法吗?”
在《现代汉语词典》中,“懂”义为“知道、了解”。那么,对于除法,学生应该“知道、了解”什么?仅仅知道除法计算法则及相应的算理,行吗?
显然,当下我们所使用的除法竖式,是在既往研究的基础上对寻求除法结果所经历步骤的简约数学表达。但如果仅仅将这样的演算视为一种程序性运算,那么时间久了,操练过度了,学生们是否如机械一般,只知运作,不懂思考?如此,作为促进学生思维发展的数学教学,作用又何在?
更进一步,身处“百度一下就能知道”的时代,身处“计算器”随处可见的当下社会,学生为什么还要花费很长时间去学习、掌握这样的计算方法呢?
教学中,我们在重视、突出规范书写格式的同时,是否弱化了学生对“尝试、调整、优化”这一数学学习、数学研究中极为重要的解决问题的方法与精神的感悟?相较于那些能完美进行除法竖式计算的学生,我们是否更应夸赞那些能及时调整、修正直至寻找到正确结果的学生?
二、对“除法竖式”的深思
基于以上追问,我以为,我们必须再次审视、剖析作为基本运算的除法,尤其是于现在的我们看来,极具数学简约美与形式美的除法竖式,除其外显的程序性算法外,其间还蕴含着怎样的数学思想、方法与精神。
“已知两个因数的积与其中一个非零因数,求另一个因数的运算,叫做除法。”显然,除法的定义源自于乘法,即除法是乘法的逆运算。《数学课程标准(2011版)》对第二学段“数的运算”部分的教学也提出了这样的要求——“在具体运算和解决简单实际问题的过程中,体会加与减、乘与除的互逆关系。”
回顾除法竖式的发展历程,(见前图)不难发现,当下我们所学习的除法竖式,正是先辈们对“如何高效、简洁地‘求另一个因数’”这一问题反复思考、不断优化后的智慧结晶。除法,特别是除法竖式,是一个不断尝试(估算、对比、调整)并逼近结果的过程。
是的,除法的竖式计算仍然只是一个寻找结果的过程。既然是过程,我们就不应也不能对其间的书写、首次正确率提出过高的要求。而这,往往又会被熟悉教材、熟稔教学过程的我们所忽视。其实,凡事总可能会出错,没有错又哪来的对?或者说,没有经历过“错”的对,往往会来得不够深刻。
我想,如果我们允许学生在除法竖式计算的过程中“错”,鼓励他们在“错”上继续调整、完善,在这样的过程中,他们是否更易理解除法竖式为何要写成这样,更能感悟于尝试、对比、调整的往复中不断逼近真相的治学方法,体会竖式中所蕴含的孜孜不倦、精益求精的治学精神。亦如老子所说,“天下难事,必作于易。天下大事,必作于细。”
于是,就有了上面这样一节“特殊”的复习课。其实,不仅仅在学完除法后我会上这样的复习课,在平面图形面积计算、运算律、数的认识……学习之后,我都会上一节“特殊”的复习课。因为,很多时候,学生的数学学习都是站在前人的肩膀上,理解、掌握那些历经几百甚至是几千年探索总结出的数学成果。教材的编排、教师的教学总是竭力将这些数学成果掰开、揉碎,力图用最恰当的方式、最短的时间、最高的效率让学生掌握。然而方法易得,思想难悟,如果经历不充分、思考不深入、理解不透彻,学生是很难深刻感悟这些数学成果的优越性以及其间蕴含的思想、方法、意志、品质与精神的。
那么,不妨带着学生在此驻足,回首吧!正所谓“众里寻他千百度,蓦然回首,那人却在,灯火阑珊处!”
