培养推理能力 渗透代数思维

罗 丹

【教学内容】

浙教版二年级下册第77 页“智慧乐园三”。

【教学过程】

一、创设情境，导入新课

师：同学们听过《曹冲称象》的故事吗？大象那么重，曹冲是怎样称出大象有多重的？老师这里有几幅连环画，请你配合画面来讲一讲。

（学生结合画面，口述故事）

师：石头的质量等于大象的质量，它们是等量关系，相等的量就可以相互代换。今天我们就向曹冲学习，用等量代换来解决问题。（板书课题）

二、自主探究，解决问题

1.初步感悟“中间量”。

师：从图中你发现了哪些数学信息？

生：1 个菠萝的质量等于2个梨的质量，1 个菠萝的质量也等于4 根香蕉的质量。

师：根据这两个等量关系，你能提出什么数学问题？

生：两个梨的质量等于几根香蕉的质量？

生：一个梨的质量相当于几根香蕉的质量？

师：这两个数学问题你们能试着自己来解决吗？四人小组为单位，借助1 号学具袋中的学具（两架天平图片、香蕉、梨图片若干）摆一摆、换一换、说一说。

（小组活动：边换边说）

师：你是怎么换的？怎么想的？

生：因为1 个菠萝=2 个梨，1个菠萝=4 根香蕉，所以2 个梨=4根香蕉，1 个梨=2 根香蕉。

师：我们知道1 个菠萝=2 个梨，1 个菠萝=4 根香蕉，所以推断2 个梨=4 根香蕉，这是因为？

生：因为2 个梨和4 根香蕉都等于1 个菠萝，所以它们质量相等。

师：那么从2 个梨=4 根香蕉推断出1 个梨=2 根香蕉，又是因为——

生：两边都取一半，2 个梨变成1 个梨，4 根香蕉变成2 根香蕉。4÷2=2，每个梨都等于两根香蕉。

师：在你们摆的时候，梨和香蕉本来没有关系，是通过谁帮它们找到联系的？

生：菠萝。

师：菠萝就是一个中间量（板书），它就像一座桥。而这个中间量是借助等量找到的（板书：等量）。有了这座桥，我们就可以用换一换的方法，把本来没有联系的数量建起联系，从而解决问题了。

2.进一步体会不同的“中间量”。

师：水果交换大会还在继续，看图说说你知道了什么？能提出什么问题？

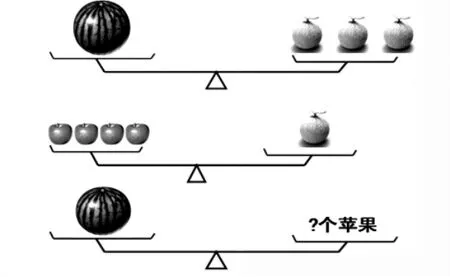
生：1 个西瓜=3 个哈密瓜，1个哈密瓜=4 个苹果。

生：一个西瓜可以换几个苹果呢？

师：你能尝试用不同的方法解决图中的数学问题吗？四人小组说一说、算一算，有困难的也可以利用2 号袋中的学具（西瓜、苹果、哈密瓜图片若干，天平图片）换一换。

（小组活动：边换边说）

师：你是怎么换的？怎么想的？

生1：（投影展示）我知道1个西瓜的质量等于3 个哈密瓜的质量，1 个哈密瓜的质量又等于4个苹果的质量，所以我把第一架天平右边的哈密瓜都换成苹果，按1 个哈密瓜换4 个苹果，3 个哈密瓜能换3×4=12 个苹果。

师：这位同学的方法借助中间量哈密瓜把第一个天平上的哈密瓜都换成了苹果，你还有不同的想法吗？

生2：1 个西瓜的质量等于3个哈密瓜的质量，1 个哈密瓜的质量又等于4 个苹果的质量，我可以给第二架天平右边增加2 个哈密瓜，那么左边应该同时增加8 个苹果，这样3 个哈密瓜的质量就等于12 个苹果的质量，因此1 个西瓜的质量就等于12 个苹果的质量。

师：生2 的方法与生1 的方法有什么不同？

生：生1 用1 个哈密瓜做桥，把西瓜和苹果联系起来；生2 是用3 个哈密瓜做桥，把西瓜和苹果联系起来的。

师：解决问题的方法和策略常常不是唯一的，从不同的角度思考问题，思路会更加开阔。

师：刚刚罗老师还注意到，有很多同学没有摆实物图片、不用动手换就得出了结果。你们又是怎样做到的呢？

生：我在脑子里想，1 个哈密瓜换4 个苹果，3 个哈密瓜能换3个4，也就是3×4=12 个苹果，所以1 个西瓜的质量等于12 个苹果的质量。

师：回忆我们刚才在水果交换大会上怎样换的？

生：观察、找等量关系；借助中间量；代换。

三、巩固练习，拓展应用

1.以物换物。

师：等量代换的方法古已有之！古代社会，人们就通过以物换物的方式交换自己需要的物品。

课件出示图片——

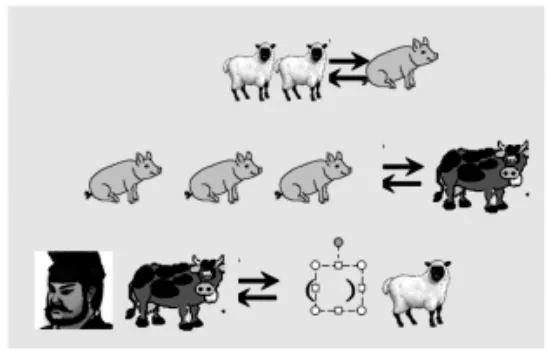
师：请同学们先独立解决，再交流汇报。

生：1 头牛=6 只羊。

师：谁能说说你是怎么换的？

生：我是这样想的：从图中知道2 只羊=1 只猪、3 只猪=1 头牛。在第一个等式右边加1 只猪，左边就要加2 只羊，加两次后得到：3 只猪就=6 只羊，而3 只猪=1 头牛，所以1 头牛=6 只羊。

师：他还想用狗也来换一换，你能帮帮他吗？

生：观察这三个等量关系，猪和牛之间的等量关系与这道题无关，是无关信息，可以去掉。

师：你们同意吗？去掉无用的干扰信息，更加有利于我们解决问题。谁来接着说？

生：要想知道狗与猪之间的等量关系，中间的桥梁就是它们分别和羊的关系。第三个等式中，1 只羊=2 只狗，那么2 只羊=4 只狗。再和第一个等式联系起来，4只狗=1 只猪。

师：经过这样的换物活动，你们有什么体会？

生：确定中间量很关键。

生：条件很多的时候，要根据自己的需要，找到有用信息，去掉无关信息。

2.题目大变脸。

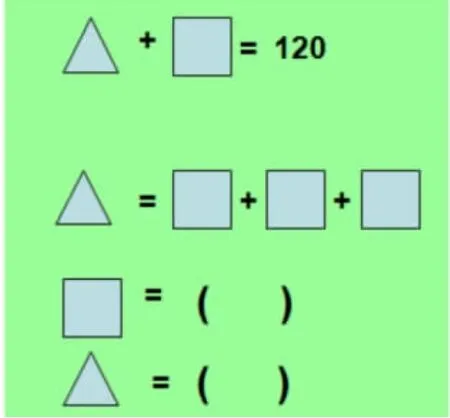
师：这个等式你能解决吗？

生：从题目我知道了：△+□=120，而1 个△=3 个□。这样，我可以把第一个等式中的1 个△代换成3 个□，等式变成了4个□=120, 那么1 个□=120÷4=30，1 个△=30×3=90。

师：同学们真了不起，用等量代换的方法，我们可以解决各种变化的问题。

3.茶水问题。

师：换了这么久，我们去茶水间歇歇吧。

课件出示图片——

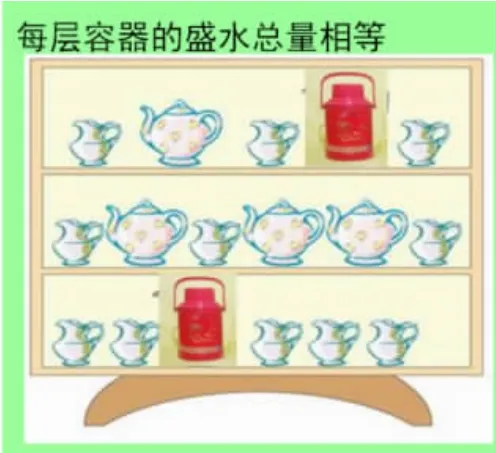
师：观察三层容器，说说有什么相同点与不同点？

生：相同点是每层容器的盛水总量相等，不同点是每层中盛水容器的情况不同。

师：它们之间也存在着等量关系，同学们能不能借助等量关系发现一个暖瓶等于几个茶壶的盛水量？一个茶壶等于几个水杯的盛水量？

生：我先看的是1、2 两层，因为每层容器的盛水总量相等、每种容器的盛水量也相等，如果把这两层相同的容器同等数量地划掉，总盛水量还是相等。我把1、2层的3 个水杯和1 个茶壶都划掉了，得到1 个暖瓶等于2 个茶壶的盛水量。

生：我是通过1、3 层划去相等的量，得到水杯和茶壶盛水量的关系。大家看，我们把1 个暖瓶和3 个水杯都划掉，会发现1 个茶壶等于2 个水杯的盛水量。

生：既然1 个暖瓶=2 个茶壶，而1 个茶壶=2 个水杯，那么我们还可以推断出1 个暖瓶=4个水杯。

师：同学们说得太好了。在解决茶水问题时，你又有什么新的心得？

生：可以通过划去同样的数量找到等量关系。

生：原来相等的数量，抵消一部分后仍然相等。

四、总结提升，课后延伸

师：本节课你有什么收获？

生：我学会了等量代换。

生：在解决等量代换问题时，找到中间量很重要。

生：对于已知的等量关系，我们可以在等号两边同时加减相等的数量，也可以同时乘几倍，有时，还可以对相等的量进行比较，抵消相同的部分……我们看到相等的关系后还可以变化出更多的相等关系，帮助我们解决问题。

师：我们可以运用各种方法实现等量之间的代换。和曹冲一样，将不可能的任务变得可能。