涂色问题有妙招
2019-01-23郭家豪
郭家豪
星期天,我正津津有味地看着一本趣味数学课外书。突然,一道有趣的题吸引了我的注意。题目是这样的:有一个由27个相同小方块搭成的正方体,把这个正方体的表面都涂上颜料,那么涂到一面的小方块有几个?涂到两面、三面的呢?
我饶有兴趣地研究起来。既然是在表面涂色,那就得除去不在表面的中心块,能涂色的就只有表面的26个小方块。我在草稿纸上画起草图来,一边画一边想:咦,这个图形好熟悉啊!我在脑海里搜索了一遍,忽然灵光一闪:这不就是我平时常玩的三阶魔方吗?于是我马上找来了三阶魔方,连草图都不用画了,直接在魔方上比画了起来。
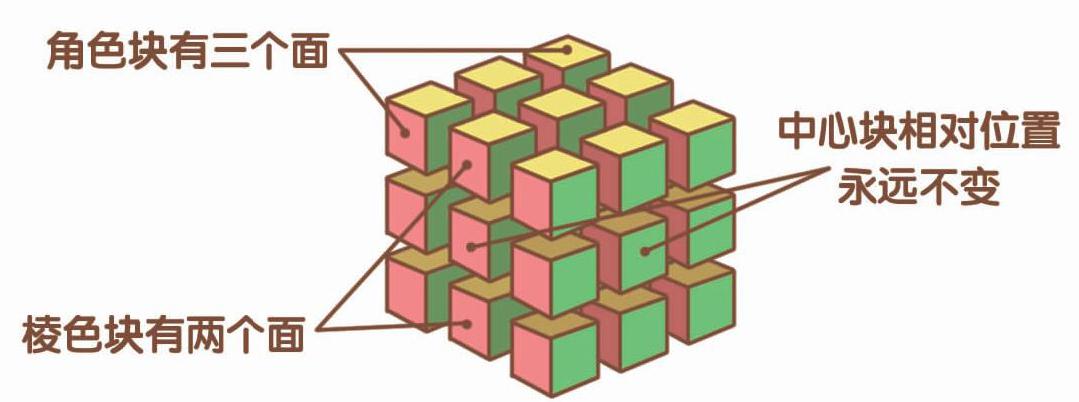
三阶魔方的表面(如上图)是由6个中心块、12个棱色块和8个角色块组成的,合起来,表面一共有6+12+8=26(个)小方块。
看三阶魔方的每个中心塊,我们只能看到一面,而每个棱色块我们可以看到两面,每个角色块我们能看到三面。所以,能涂到一面的小方块有6个,能涂到两面的有12个,能涂到三面的有8个。
运用魔方解这类题真是简单,我马上把我的新发现告诉了妈妈。妈妈听了后给我竖起了大拇指,但转而又问我:“要是组合正方体的小方块数量增多,又该如何计算呢?”我还没回答,紧接着妈妈就给我出了一道题:“由125个相同小方块搭成的正方体,能涂到一面、两面、三面的小方块各有几个?”
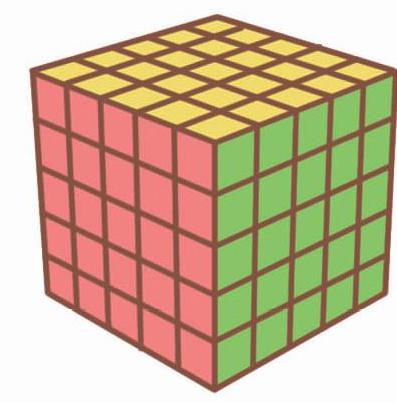
听完妈妈的话,我马上思考了起来。因为125=5×5×5,所以它的形状就是五阶魔方的形状。
因为魔方8个顶点上的8个角色块是不变的,所以不管正方体由多少个小方块搭成,能涂三面的小方块都只有8个。
而能涂两面的棱色块这时已经有了变化,棱色块个数的计算方法是用正方体的每条棱的小方块总数减去每条棱的2个角色块,再乘以正方体的总棱数12。也就是说,能涂两面的小方块有(5-2)×12=36(个)。
最后来看能涂到一面的中心块数量,也变多了。用正方体一个面的中心块个数乘以正方体的总面数6,就能得出能涂一面的小方块有3×3×6=54(个)。
由此我得出结论,不管组合正方体的小方块数量有多少,只要巧妙运用魔方的构造,求出魔方的中心块、棱色块、角色块的个数,就能求出能涂一面、两面、三面的小方块个数了。
我把得出的结果告诉了妈妈,妈妈连连称赞,夸我善于观察,好样的。
数学世界真奇妙,只要你善于观察,你就会发现再难的题也有小妙招。
钱多多 1月6日 09:20:12
难怪我思考半天都没解出这道题,原来是少了魔方这个道具,待会我就去买一个。
许浩然 1月6日 10:33:13
没道具可以画出来嘛,考试时可不给你拿什么道具。
周小诺 1月6日 11:45:10
告诉你们吧,对付这样的题目,我有万能公式:如果每条棱有n个小方块,那么能涂一面的有[(n-2)×(n-2)×6]个,能涂两面的有[(n-2)×12]个,能涂三面的有8个。
