开放性练习，让学生跳出知识学数学

2020-12-02孙贵合

小学教学设计(数学) 2020年11期

孙贵合

如果离开了知识本身，数学一定是无源之水，无本之木。那如何能够跳出知识呢？知识本身是一个结果，除了对于考试，可能在学生的一生中，很少能用到了。比如我们学习的《圆的面积》《三角形的面积》《圆柱的体积》《圆锥的体积》等等，认真回忆一下，除了在课堂中，在生活上我们什么时候用到过？虽然知识很少能用到，但在学习过程中所收获的动手能力、数学思想、学习经验，在学生今后的生活中是随处可见的：当遇到一个新的问题，如何去解决，可以把它转化成以前解决的问题；看到一件事情，能够快速地分析出与哪些信息有内部的联系等等。可见表面看起来不重要的学习过程，却对学生的成长起着至关重要的作用。这也正是“无用之用，方为大用！”林清玄正是留心生活中的点点滴滴，于残花片叶中发出无限的哲思；史铁生独对地坛，沉默不语，悟出生死的真谛……因此在课堂教学中，当教师真正从人的发展角度去思考教学，就能够跳出知识教数学了，学生也就能够跳出知识学数学了。

案例一：《数对》。

在教学这一内容时，更多的教师注重到了本节课的知识点，如何用数对表示位置，以及纵向知识之间的联系：一个数字，可以表示线上的位置；两个数字，可以表示面上的位置；三个数字，可以表示体上的位置；以及数对的产生、感受数对的作用等等。但数对又与哪些知识有内部的联系，却很少有人去思考和实践。于是在课后练习环节我设计了这样的题目：（）+（）=12，括号里的两个数所组成的数对，在网格图上连在一起会是什么样子？相信很多教师看到这道题目也是先想一想再给出答案。为什么呢？是因为没有考虑过这样的问题。学生思考数对的位置，是巩固本节课所学知识，进一步思考数对所表示的点连在一起的图形时，即是“数与形”在学生头脑中真正的建立联系。当然还可以出：（）×（）=12，括号里的两个数所组成的数对，在网格图上连在一起会是什么样子？相信教师们看到这道题目，都会毫不犹豫地说出点连在一起的样子，是因为这是六年级正反比例中的教学内容，等学生到六年级学习这部分知识的时候，自然感受到了“数与形”之间的联系。所以教师们都知道，只是没有考虑教学知识以外的内容，当我们能够用心去考虑知识之外的内部联系时，我们的课堂教学自然就有了新意，同时让学生更充分地感受知识之间千丝万缕的关系。其实不光加法、乘法能够建立“数与形”之间的联系，减法和除法也可以建立这样的联系。

通过这道题不难发现知识之间都是有联系的，这需要我们自己去思考，只有用心去理解，才能够发现，也只有教师发现，学生才能够感受。

教材中提到了“数与形”，所以在这一部分教师的思考也就深入了，其实除了“数与形”两种不同领域的知识之间有着密不可分的联系之外，在数学教学中，还能够找到很多的联系，这就像史宁中教授所提出的，我们要培养的学生应该能够“用数学的眼光观察世界，用数学的思维分析世界，用数学的语言描述世界。”同样这也需要我们教师能够做到，如果教师都做不到，怎么能够培养出这样的学生呢？这种意识的培养是必不可少的，但这种联系的用时不能过长，用力不能过重，不能喧宾夺主，否则就得不偿失了。

案例二：《三角形分类》。

本节课涉及两个知识点：按边分和按角分。如何能够把按边分与按角分有机整合在一起呢？于是很多教师便结合三角形的特点，得出了很多新的名称：等腰直角三角形、等腰钝角三角形、等腰锐角三角形。名称放在一起，就是知识内在联系在一起了吗？我想不是这样简单的，应该抓住知识内部建立联系，即使学生现在还不够清楚明白，但等到将来再次接触这一部分相关知识时，能够很快地与今天所学习的知识之间建立联系，不也是一件很好的事情吗？虽然今天没有感受到它的作用，但为学生的后续发展，以及学生知识体系的建立，打下基础也是功不可没的。于是在课堂最后，我设计了这样一道题目：

师：同学们，看看这是一个什么三角形？

生：等边三角形。

师：还是一个什么三角形？

生：锐角三角形。

师：如果把三角形的两条边延长，它会变成一个什么三角形？

生：还是锐角三角形、还是等腰三角形。

师：如果我再延长呢？

生：还是锐角三角形、还是等腰三角形。

师：在这个变化过程中，你发现了什么？

生：我发现上面的角在不断地变小，而下面的两个角在不断地变大。

师：那你们说，下面的两个角，不断变大再变大，最大能到多少度？

生：89.9°。

师：要是再大呢？

生：89.99°。

师：你们为什么不说90°？

生：不可能到90°，要是90°，左边和右边就平行了，就不能围成三角形了。

（培养空间观念的同时，为学习三角形的内角和打下基础）

师：还发现了什么？

生：都是锐角三角形，都是等腰三角形。

师：为什么都是锐角三角形和等腰三角形呢？难道就没有直角三角形和钝角三角形吗？

生：刚才总在延长，要是缩短一下试试呢？

师：缩短一下，还真的有直角三角形和钝角三角形，看来我们思考问题时，有时还要换个方向。

【思考：换个方向思考问题很重要，成人在解决问题遇到困难时，很多时候都会停下来去做点别的工作，然后换个思考方向，会收到意想不到的效果。曾有人用苍蝇和蜜蜂做过对比实验，分别把数量相等的蜜蜂和苍蝇装到同一个玻璃瓶里面，然后将玻璃瓶平放，瓶底朝着窗户光亮的方向，瓶口是敞开的。因为昆虫都有趋光性，很快，实验者就看到蜜蜂都聚集在瓶底，企图找到出路，它们不断地撞击瓶底，直到最后筋疲力尽，累死在瓶子里；而那些苍蝇，在最开始也都聚集到瓶底处，撞击几次后，就开始在瓶子里盘旋，向另一个方向飞去，不到两分钟，就纷纷找到瓶口，四散飞走了。

蜜蜂的命运固然可悲，但其反映出来的问题却耐人寻味，蜜蜂在判断出口的方向时，只是凭借过往的“经验”按照一个方向思考问题，经验告诉它光亮处才有可能是出口，墨守成规、生搬硬套才是这起蜜蜂“惨剧”的主要原因。而苍蝇之所以能够成功，是因为在遇到困难时懂得掉头，换个方向思考，所以换个方向去思考问题非常重要。现实中不也有很多这样的情形吗？固执己见、经验主义、被惯性思维严重束缚而不自知。在日新月异的时代发展过程中，无论个人还是企业，都会面临各种情形的改变或者不确定的状态，如果不能因发展变化而进行创新和改变，很可能终将被淘汰。最好的应对方法就如同那些苍蝇一样，敏锐地在变化中找到发展的新途径，既然无法预测变化的发生，那就需要掌握随机应变的本领，在变化中不断调整自己，这样才能取得主动，走向成功。通过一个简单的练习，让学生能够感受多角度思考问题，是非常值得的。】

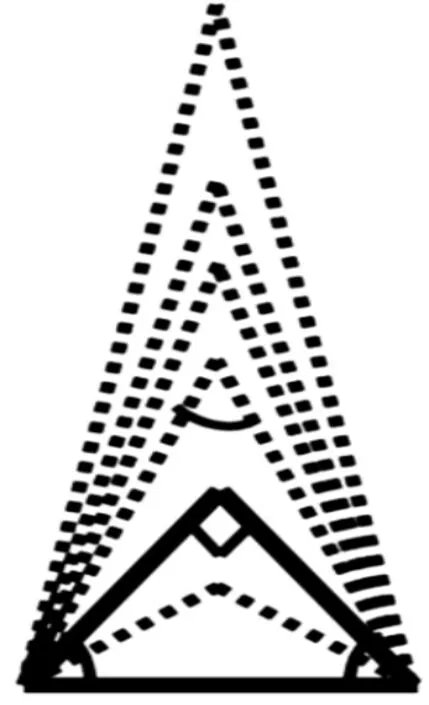
师：那你看这些三角形在一起像什么图案？

生：像金字塔、像屋顶……

师：你们看，和这个像不像？

师：这是2008年西班牙世博会主题馆水塔馆，让我们共同期待世博会带给我们更多的精彩。

【思考：让学生感受数学与生活的联系时，更让学生关心国家大事。风声雨声读书声声声入耳，家事国事天下事事事关心。】

看过之后，可能有些教师已经忘记本节课的主题，联系让学习更深刻，深刻在哪里？其实内在联系已经在悄然发生着，只是我并没有告诉学生，为什么您也没有发现呢？这就是一种教师经常会出现的问题，常教低年级的教师，过几年连高年级的题都不太会做了；小学教师教几年会发现，中学的题已经不会做了；教几年中学下来，会发现小学的题和高中的题不会做了……为什么会出现这种现象呢？是因为我们过多地关注所教学内容，而对于非主要教学内容已经不再看、不再学了，自然时间一长便忘记了。小学教师看到这幅图没有什么感觉，但如果把这幅图给中学数学教师看，他一定会说，这节课在学习“三角形的分类”。到中学时，学生再次学习“三角形的分类”时，一定会用到这幅图，只是今天的图片比较特殊，到中学还会穿插不等边三角形，认真观察这幅图不难发现：直角三角形具有勾股定理，即a2+b2=c2，而所有的锐角三角形a2+b2＞c2。只有这样的分类方法，才是真正地把三角形按角分、按边分，从知识体系上真正地结合在一起。有的教师会说，这么难的知识学生是否能够接受得了？学生一定是接受不了的，而且这些知识我也不会讲，我希望等到有一天，学生来到中学，再次学习《三角形的分类》看到这幅图时，能够想到“这幅图我见过”就可以了，使学生把小学所学的知识与中学所学习的知识进行有机整合。