稳定平台地理坐标系与空间大地直角坐标系的转换

翟玉健，李 敬

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

空间直角坐标主要是指笛卡尔直角坐标系，但是针对不同的平台，笛卡尔坐标系的坐标轴略有不同。机(弹)载坐标系又分欧美系和苏式坐标系，加之常用的舰载坐标系，组成了常用的右手直角坐标的3种坐标系。而坐标变换主要有2种方式，一种是平移变换，另一种是旋转变换。平移变换只改变原点的位置而不改变轴的方向，旋转变换改变轴的方向而不改变原点的位置。任何系统的坐标变换都可以通过这2种变换或其中一种变换方式完成。下面就根据平移和旋转推导出舰载平台和机(弹)载平台3种地理稳定坐标系到地心直角坐标系的变换，以实现空间目标的定位。

1 变换原理

直角坐标平移是指坐标轴的指向不变，只改变坐标轴的原点位置，具体见参考文献[1]，本文具体介绍坐标旋转。

直角坐标旋转是指坐标轴原点不变，只调整坐标轴的指向，如图1所示。

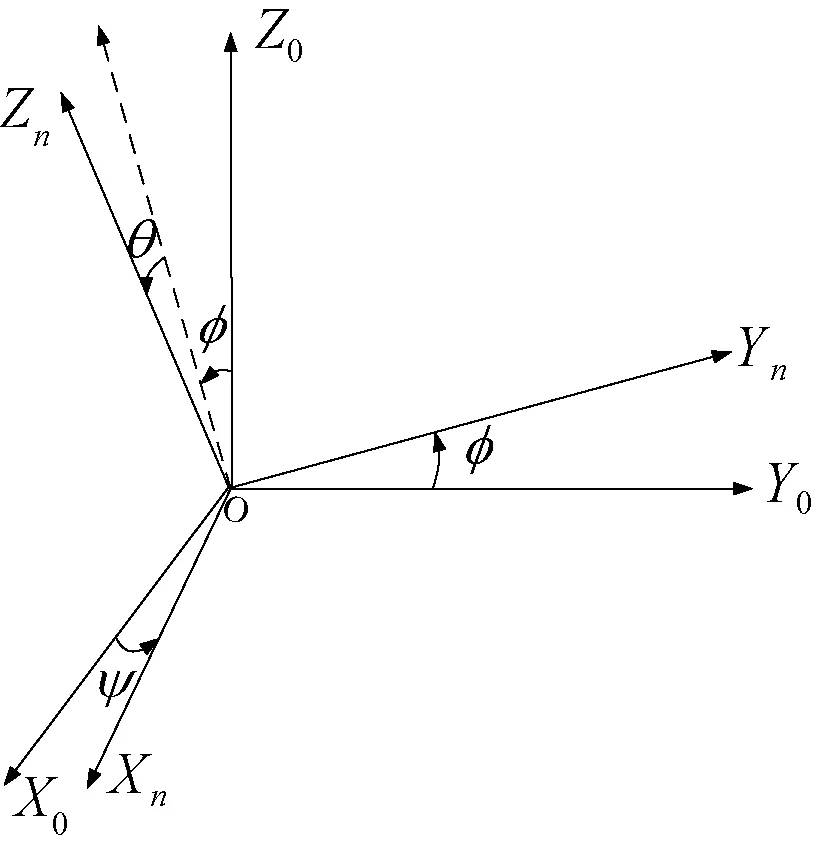
图1 直角坐标系旋转

设新坐标系Sn与原坐标系So原点一致，空间中点P在So中的坐标为(Xo，Yo，Zo)，点P在Sn中的坐标为(Xn，Yn，Zn)，则经过3次旋转有：

(1) 保持旧Zo轴不动，OoXoYo按右手规则旋转ψ角；

(2) 保持新Yo轴不动，OoZoXo按右手规则旋转θ角；

(3) 保持新Xo轴不动，OoYoZo按右手规则旋转φ角。

则：

(1)

引入旋转矩阵符号如下：

(2)

(3)

(4)

(5)

(6)

展开为：

(7)

2 稳定平台地理坐标系与空间大地直角坐标系的转换

要进行空间坐标系变换，首要确定坐标系。任何一个观测模型都是依据状态空间模型建立的，选择合适的坐标系，对于保持空间的一致性、简化计算是非常重要的，坐标系的选择将直接影响跟踪的精度和计算量的大小。WGS84大地坐标系是以地心作为椭球体中心的参考模型，具体定义和计算可以参考文献[1]。这里主要介绍空间大地直角坐标系，空间大地直角坐标系是地心坐标系，即以地球质心为原点，轴Zo与地球的旋转轴一致，轴Xo位于起始大地子午面和赤道面的交线上，在赤道面上与Xo轴正交的方向为Yo轴，见图2的OoXoYoZo坐标系。

图2 地球直角坐标系与舰载平台地理坐标系之间的旋转关系

2.1 舰载稳定平台地理坐标系与空间大地直角坐标系之间的转换

舰载体地理坐标系[2]的3条参考轴与舰载体不固连，它不随舰艇摇摆，因此是“稳定”的。它的3条参考轴的取向与地理参考系相同，在大地坐标系下Yr轴指向正北，Xr轴指向正东，由于其原点会随着舰载体一起移动，因此称它为舰载稳定平台地理参考系或相对地理参考系。设舰载体的地理位置为Or，其大地坐标系的坐标表示为(LrBrHr)，此处Br为地理维度。空间大地直角坐标系的表示为(Xor,Yor,Zor)，如图2所示。

设目标点P在舰载地理坐标系(以Or为原点)的位置为Xrt,Yrt,Zrt，如果将P点从以Or为原点的坐标系转换到以Oo为原点的(大地空间直角)坐标系下，旋转顺序为：

(1) 保持旧OrXr轴不动，OrYrZr按右手规则旋转-(90°-Br)角度，此时Zr轴与Zo平行，OrYrXr平面与OoYoXo平面平行。将旋转角度代入式(6)中的CX(φ),则旋转矩阵为：

(8)

(2) 保持新OrZr轴不变，OrXrYr按右手规则旋转-(90°+Lr)角度，此时2个坐标系就平行了。将旋转角度代入式(6)中的CZ(ψ),则旋转矩阵为：

(9)

(3) 再通过坐标平移就可以实现舰载平台地理坐标系到地心直角坐标系的转换，总的转换公式如下：

(10)

式中：LrBr为观测点Or的经度、纬度；Xor,Yor,Zor为观测点Or的空间大地直角坐标位置；Xot,Yot,Zot为目标点P的空间大地直角坐标系位置；Xrt,Yrt,Zrt为目标点P在观测点Or坐标系的位置。

用旋转矩阵符号表示如下：

(11)

根据旋转矩阵为正交阵，其逆变换的旋转公式如下：

(12)

则目标P空间大地直角坐标转换到舰载体地理坐标系下的完整转换公式为：

(13)

2.2 苏式坐标系下机(弹)载稳定平台地理坐标系与空间大地直角坐标系之间的转换

苏式坐标系下机(弹)载地理坐标系[2]OrXrYrZr的原点Or为弹载体发射点或机载雷达的观测点，Xr轴是原点Or至目标点的照准面和包含发射点的水平面的交线，指向目标点方向，Yr轴和原点Or的铅垂线方向一致，指向地球外，Zr轴和Xr、Yr轴构成右手坐标系。Xr轴与正北(N)轴有一个射击方位角Ar(机载坐标系下Ar=0，Xr轴指向正北)，设发射坐标系的地理位置为(LrBrHr)，射击方位角Ar，如图3所示。

图3 空间大地直角坐标系与苏式坐标系下机(弹)载平台地理坐标系之间的旋转关系

设目标点P在苏式地理坐标系(以Or为原点)的位置为Xrt,Yrt,Zrt，如果将P点从以Or为原点的坐标转换到以地球中心Oo为原点的坐标系下，旋转顺序为：

(1) 保持旧OrYr轴不动，OrZrXr按右手规则旋转(90°+Ar)角度，此时Zr轴指向正北(Zo轴)；

(2) 保持新OrXr轴不变，OrYrZr按右手规则旋转-Br角度，此时Zr轴就与Zo轴平行了；

(3) 保持新OrZr轴不变，OrXrYr按右手规则旋转(90°-Lr)角度，此时2个坐标系就平行了。

用旋转矩阵表示：

(14)

这与参考文献[1]中给出的发射坐标系到空间大地直角坐标系的转换公式是一致的。

(4) 再通过坐标平移就可以实现机(弹)载平台地理坐标系到空间大地直角坐标系的转换，总的转换公式如下：

(15)

根据旋转矩阵为正交阵，其逆变换的旋转公式如下：

(16)

则目标P空间大地直角坐标系转换到机(弹)体地理坐标系下的完整转换公式为：

(17)

2.3 欧美系下机(弹)载平台地理坐标系与空间大地直角坐标系之间的转换

欧美系下机(弹)载地理坐标系[3]的原点同苏式坐标系，只是坐标轴指向不同。原点Or为弹载体发射点或机载雷达的观测点，Xr轴指向当地北子午线，Yr轴垂直Xr轴指向正东，Zr轴垂直于XrOrYr平面，指向飞行器下方。如果是弹载发射坐标系，则Xr轴与指向正北之间有一个射击方位角Ar。设发射坐标系的地理位置为(LrBrHr)，则如图4所示。

图4 空间大地直角坐标系与欧美系下机(弹)载平台地理坐标系之间的旋转关系

比对图3和图4，可以看出欧美系下的机(弹)载平台地理坐标系与苏式坐标系下的机(弹)载平台地理坐标系之间差了一个90°。只要保持欧美系下的机(弹)载平台地理坐标系的OrXr轴不变，OrYrZr按右手规则旋转-90°，就变成了苏式坐标系下的机(弹)载平台地理坐标系，因此，欧美系下将P点从以Or为原点的观测(发射)地理坐标转换到以地球中心O0为原点的空间大地直角坐标系下的旋转公式顺序是：

(1) 先保持OrXr轴不变，OrYrZr按右手规则旋转-90°；

(2) 按照2.2节中(1)～(3)的旋转顺序进行旋转即可，用旋转矩阵表示为：

CY(90°+Ar)CX(-90°)

(18)

(3) 再通过坐标平移就可以实现机(弹)载平台地理坐标系到空间大地直角坐标系的转换，总的转换公式如下：

(19)

根据旋转矩阵为正交阵，其逆变换的旋转公式如下：

(20)

则目标P空间大地直角坐标系转换到欧美系下机(弹)体地理坐标系下的完整转换公式为：

(21)

3 验 证

假设观测点的大地坐标位置是东经119°58′42″，纬度39°58′20″，高度架设27 m，目标点的大地坐标位置是东经119°52′32″，纬度39°59′32″，高度架设10 m，则将其转换到空间大地直角坐标系下的位置见表1。将观测点和目标点的位置信息以及观测点的经纬度值代入式(13)、式(17)和式(21)可以求得表2中目标在观测坐标系下的位置。

表1 空间大地直角坐标

在地理坐标系下一点P，用雷达测量坐标系[4]表示为P(R,α,φ)，方位基准线位于过原点O的水平面内，指向正北；斜距R为原点O与目标点P之间的距离；俯仰角φ为目标视线与水平面夹角，向上为正；方位角α为目标视线在水平面投影与方位基准线间夹角，顺时针为正。设欧美系和苏式坐标系下机(弹)载的射击方位角Ar=0，这样3种平台的雷达测量坐标系就统一了。 因此将目标分别通过3种坐标系的平移和旋转后转到雷达测量坐标系下应该是同一个位置，具体参数见表2中目标在雷达测量坐标系下的位置。

表2 目标在各平台地理坐标系下位置

4 结束语

稳定平台地理坐标系与空间大地直角坐标系的转换是目标定位的主要计算方法，参考各种文献都有提及某个转换公式，但没有具体全面给出转换公式所属的坐标系定义，例如文献[1]中只给出了发射坐标系的转换矩阵。本文系统、全面、明确地对3种坐标系进行定义，根据坐标旋转的原理推导三种坐标系下稳定平台地理坐标系与空间大地直角坐标系的正反转换公式，并给出了验证，证明转换的正确性。