平台摇摆下舰载相控阵雷达被动探测测角误差仿真

朱 润，沈 凡，高 清

(中国船舶重工集团公司第七二四研究所，江苏 南京 211153)

0 引 言

角度测量是相控阵雷达接收系统重要任务之一。被动超视距探测侦收的辐射源信号幅度受双方天线方向图调制以及传输路径损耗起伏影响，难以通过多脉冲积累的方式获得高精度测角结果。单脉冲测角仅凭单个脉冲信号即可完成辐射源精确测角，故被动超视距雷达常采用单脉冲测角方法对辐射源进行测向。

文献[1]分析了单脉冲测角理论测角精度。文献[2]对方向图切割与相控阵天线安装精度对测角精度影响进行了详细分析研究。文献[3]对不同信噪比对被动相控阵雷达测角精度影响进行了分析。文献[4]根据相控阵雷达波束扫描导致波束展宽、归一化斜率因子下降等因素对测角精度影响进行了仿真。本文对舰载平台摇摆引起信号相对相控阵天线入射俯仰角变化，进而导致单脉冲比幅测角误差进行了仿真研究。

1 比幅法单脉冲测角原理

相控阵雷达所采用的单脉冲测角方法主要有3种：幅度比较法、相位比较法、幅度相位比较法。被动相控阵雷达一般采用双波束比幅法对入射信号进行测角[5]。2个相互交叠的波束方向图分别为F1(θ)、F2(θ)，如图1所示。图中θ1、θ2分别为2个波束最大增益所在位置。

图1 相互交叠的2个接收波束

对于θ方向入射的信号，2个波束接收到的信号幅度比值为：

(1)

式中：G1、G2分别为2个波束对对应接收通道增益。

采用查表方法在预先存储的K(θ)与θ1、θ2之间位置对应关系表中，获取入射信号所在方位。对于3 dB交叠的2个波束，当信噪比为S/N时，单脉冲双波束比幅测角误差的理论极限为：

(2)

式中：θ3 dB为波束3 dB宽度；工程应用中，系数K一般取0.6～0.8。

2 坐标系转换

舰船平台罗经都采用卡尔丹环架结构，舰船地理坐标系到甲板坐标系的坐标变换必须按航向变换、横摇变换及纵摇变换的顺序进行。舰船地理坐标系OXYZ至甲板坐标系OXdYdZd变换步骤如图2所示。最后完成甲板直角坐标系到阵面坐标系的变换。

图2 舰船地理坐标系至甲板坐标系变换

文献[6]～[9]给出了详细的推导过程，可得舰船地理坐标与阵面坐标相互转换的公式为：

MA=TC×TQ×TP×TR×TH×MG

(3)

(4)

3 无纵横摇时测角仿真

相控阵雷达进行被动超视距探测时，利用了对流层对辐射源信号散射的特性，故接收信号时可认为信号均从大地0°仰角入射。为解决舰船平台摇摆对被动相控阵雷达接收的影响，对固定阵相控阵雷达，往往采用俯仰宽、方位窄的扇形波束作为接收波束，此时可保证方位测向满足精度要求，且俯仰宽覆盖，在舰船摇摆时，保证一定的接收增益。

3.1 方向图仿真

采用矩形平面阵，包含6行×60列阵元。每行包含60个阵元，每列包含6个阵元，阵元间距离为d=λ/2。方向图仿真原理公式为[5]：

k(dr2sinθ-β)]}

(5)

考虑到提升波束方向维主副比，仿真时采用了主副比27 dB的泰勒窗。仿真频率1 GHz时相控阵天线全波位三维方向图如图3所示。

图3 全波位三维方向图

大地坐标下，1 GHz时相控阵天线全波位水平方向切割方向图如图4所示。

图4 大地坐标系下水平切割方向图

3.2 比幅曲线获取

在进行测角前需要预先获取方位-幅度比值关系表，工程中通常采用暗室实测校准后各波束方向图计算得到的比值关系表。根据文献[2]分析结论，本仿真采用大地坐标系俯仰0°对仿真的平面阵方向图进行等俯仰切割，获取比幅测角的方位-幅度比值关系K(θ)。阵面坐标下方位-幅度比值关系曲线如图5所示。

图5 阵面坐标系下方位-幅度比值曲线图

3.3 比幅测角

比幅测角过程为：依据信号入射方向，计算不同接收波束接收到信号的幅度，选择幅度最大的2个波束，计算幅度比值。依据比值查找方位-幅度比值表，获取入射信号阵面坐标，最后变换到大地坐标系，得到比幅测角结果。

仿真时，设置舰船航向为0°，阵面与艏向夹角为45°，阵面倾角为15°。当舰船平台纵横摇均为0°时，信号从大地坐标方位0°～90°、俯仰0°入射，通过仿真得到无纵横摇时测角误差曲线如图6所示。

图6 无纵横摇时测角误差曲线

由图6可见，无纵横摇时，采用双波束比幅测角方法测角误差较小，仿真误差主要来源于仿真过程中的量化误差。

4 不同纵横摇下测角误差仿真

坐标转换过程以及方位-幅度比值关系K(θ)的获取与前述过程相同。当舰船平台横摇为5°、纵摇为1°时，以及横摇为10°、纵摇为2°时，分别将仿真信号从大地坐标系方位0°～90°、俯仰0°入射，通过仿真得到测角误差曲线如图7、图8所示。由图7、图8可见，随着舰船平台纵横摇摆角度增加，测角误差明显增大。

图7 横摇5°、纵摇1°时测角误差曲线

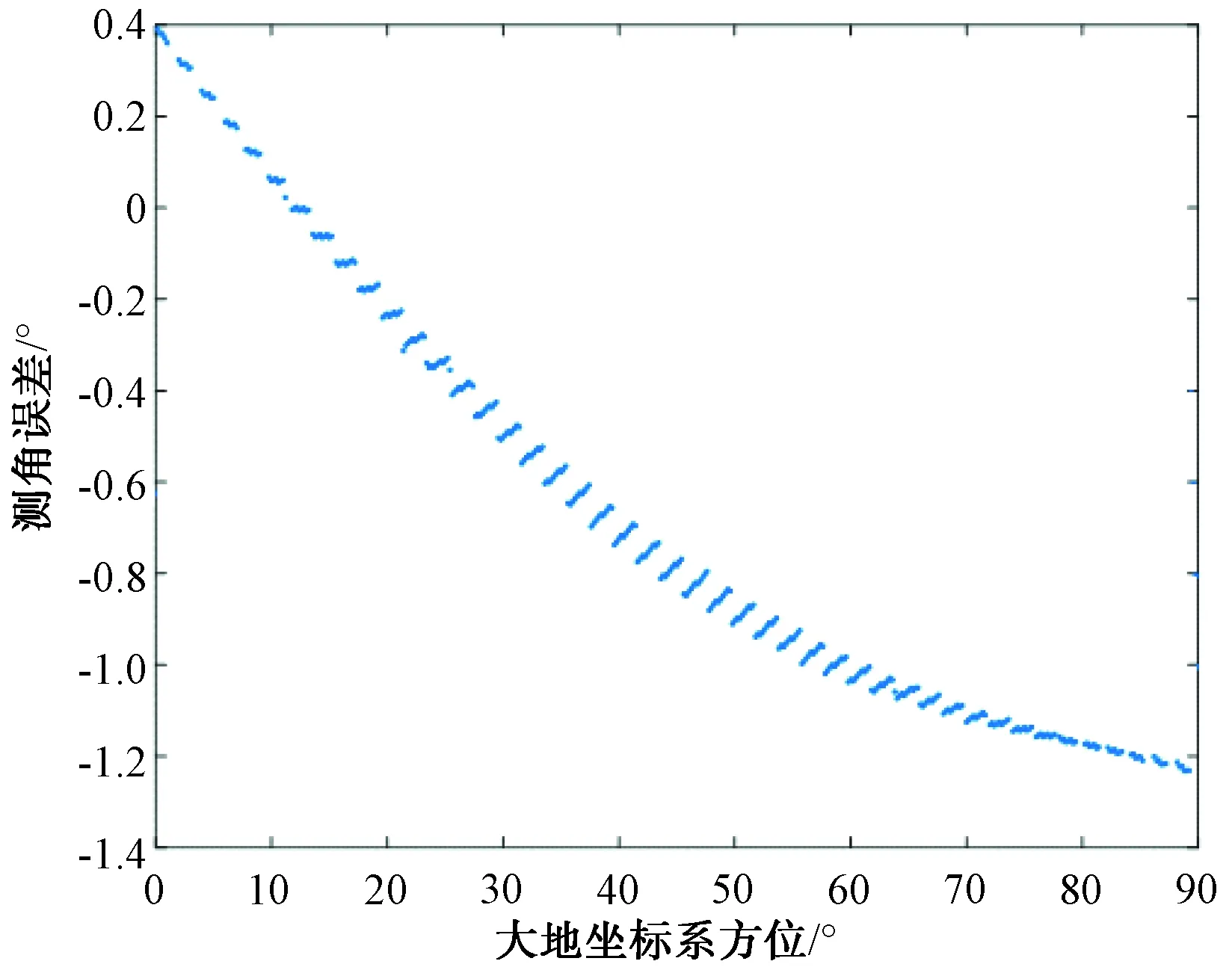
图8 横摇10°、纵摇2°时测角误差曲线

5 误差分析

方位-幅度比值关系K(θ)是在大地坐标系俯仰0°切割获得的结果，当舰船无纵横摇时，信号从大地坐标系俯仰0°入射，接收信号幅度-方位比值与K(θ)获得过程中采用的大地俯仰0°切割相匹配，故此时测角结果比较理想。当舰船有纵横摇时，大地坐标下位置相同的入射信号变换到阵面坐标后，在阵面坐标中位置发生变化。无纵横摇时，大地坐标不同方位信号入射时，各接收波束幅度关系见图9。当有纵横摇时，假设舰船平台固定，则入射信号大地坐标俯仰不再是0°。图10仿真了大地坐标系不同方位信号俯仰8°入射时，各接收波束幅度关系。

由图9、图10可见，在波束合成系数未发生变化时，同一个波束、不同仰角方位指向发生了变化，这是由于在阵中扇形波束是弯曲的，如图11所示。舰船平台摇摆时接收波束幅度比值发生变化，而幅度比值与方位关系是一一对应的，故测角结果发生变化，进而产生测角误差。

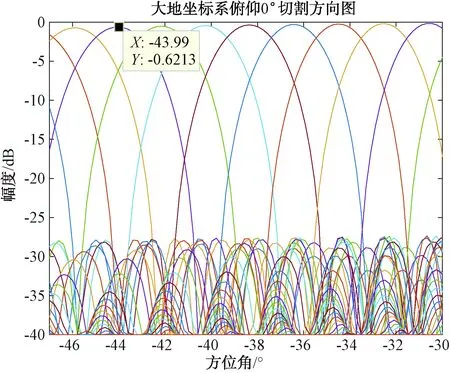
图9 无纵横摇时信号入射各接收波束幅度关系

图10 有纵横摇时信号入射各接收波束幅度关系

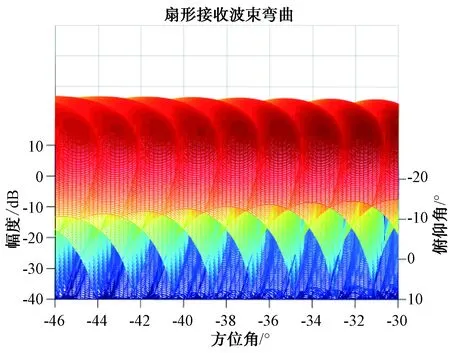
图11 弯曲的扇形接收波束

6 结束语

本文首先介绍了测角与坐标变换原理，然后对不同舰船摇摆条件下的固定相控阵雷达扇形接收波束测角误差进行了仿真和分析。从仿真结果来看，随着舰船摇摆程度加大，测角误差也随之增大。后续工作需要对如何降低平台摇摆对测角精度的影响进行进一步研究。本文对被动超视距相控阵雷达测角误差分析提供了有力支持。