化归思想在一类函数问题中的应用

成都师范学院数学学院 (611130) 王成强

化归，即将一个数学问题转化成一个数理逻辑等价的新问题的思想与方法的集合.化归思想与转化技巧是学习高中数学中必须掌握的本领之一；借助于化归思想与转化技巧解答数学问题是学习高中数学中必须积攒的数学活动经验.函数综合题形式丰富多样，成功处理此类问题需要学生具有很高的转化与化归能力、逻辑思维能力、科学计算能力、空间想象能力等.概因于此，“函数与导数”是学习高中数学难点[1].借助于转化与化归解答函数综合题，能帮助学生加深理解待处理的问题，加深认清问题的本质.本文基于化归思想，构造辅助函数，将三道涉及证明不等式的函数综合题，转化成极值点偏移问题，最后，利用该方向的惯用方法解答新得的极值点偏移问题，从而完成对原问题的解答.

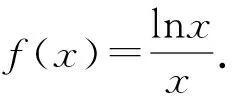
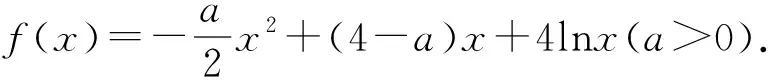
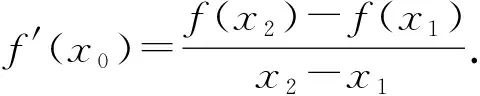
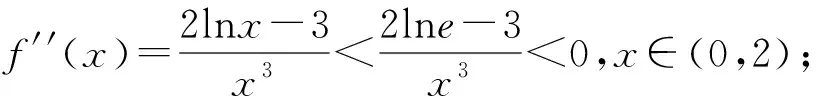
1 借助极值点偏移问题中的想法处理问题1-3

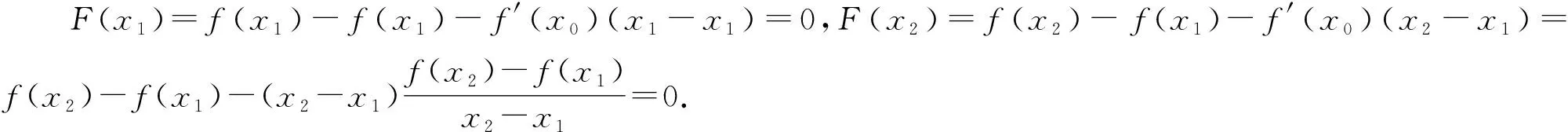
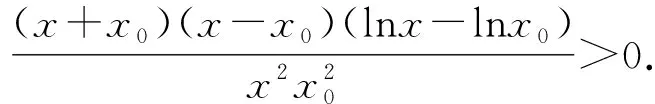
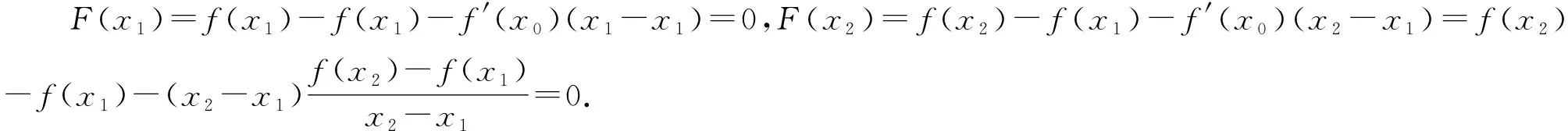
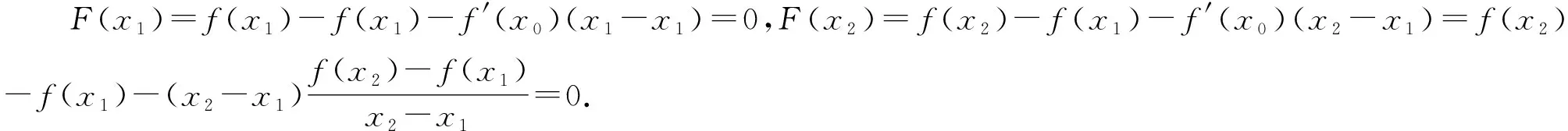
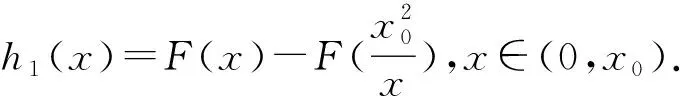
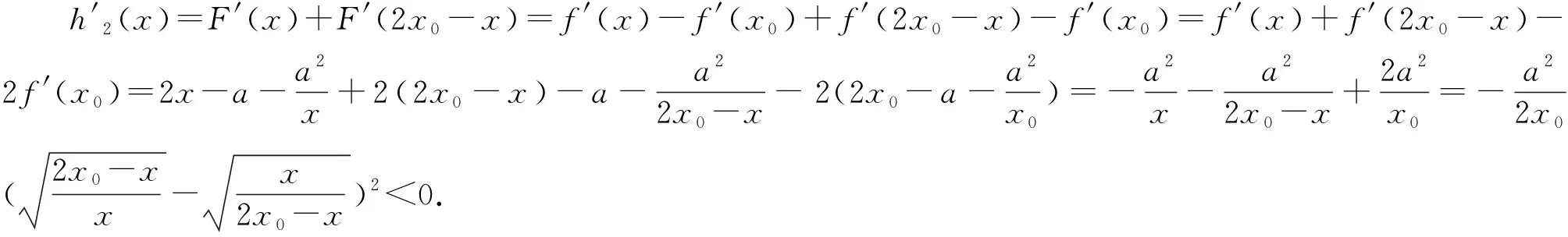
注1 证明问题1-3过程中引入的辅助函数F(x)都可以替换成F1(x)=f(x)-f′(x0)(x-x1)；

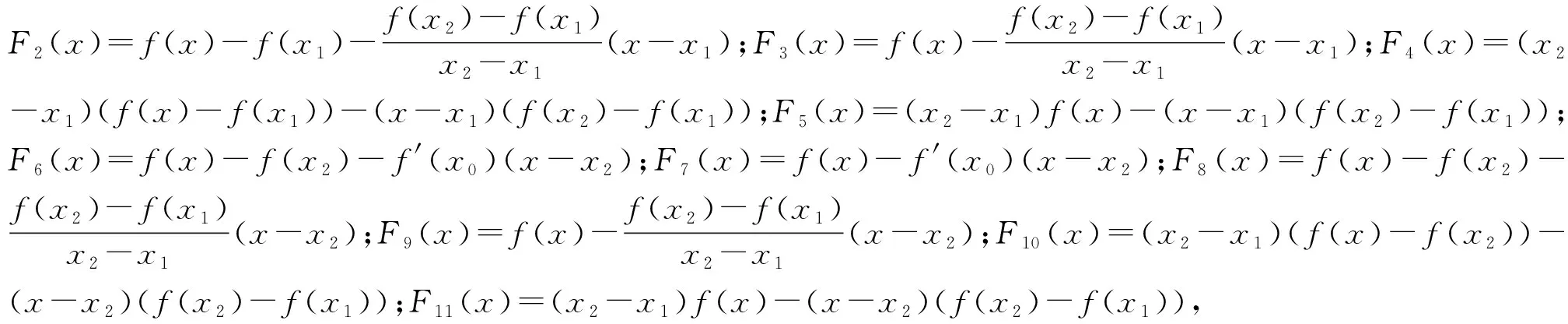
F1(x1)=F3(x1)=f(x1)=F1(x2)=F3(x2)，F2(x1)=F4(x1)=0=F2(x2)=F4(x2)，F5(x1)=(x2-x1)f(x1)=F5(x2)，F6(x1)=F8(x1)=F10(x1)=0=F6(x2)=F8(x2)=F10(x2)，F7(x1)=F9(x1)=f(x2)=F7(x2)=F9(x2)，F11(x1)=(x2-x1)f(x2)=F11(x2).

2 结束语

问题1-3具有函数综合题的典型特征，创新性充分，数学情境营造合理，是各地高三数学模拟考试的热门问题.模拟考试试卷的答案都是借助于化归思想，将问题中的不等式转化成新的不等式，之后，借助于齐次化方法，再将问题转化成函数的单调性问题，最后采用导数分析法，断定函数的单调性并完成问题的证明.本文提出的方法也是基于化归思想，但与现存解答不一样的是，本文是将问题转化成极值点偏移问题.这样处理的优点有二：其一，与现存解答相比，本文的计算更加具有目的性，且计算量相当于或略低于现存证明方法中的计算量，其二，借助于本文的方法，把问题转化成极值点偏移问题，能帮助加深学生对问题的理解并认清问题的实质，能“引诱”学生尝试利用极值点偏移问题中的方法处理问题，过程中不仅累积了解题经验，也反过来加深了对极值点偏移问题的理解，能帮助学生将学过的知识“嵌入”更少的知识模块中，从而使学过的知识更加系统化.