解题中应展现学生的思维碰撞——以一道椭圆试题教学为例

江苏省无锡市第一中学 (214000) 吴明飞

圆锥曲线试题一般都是秉承简洁、灵动的命题风格，呈现了许多设问通俗、内涵丰富、解题多样的好题.通过这些试题既考查了学生的基础知识和基本技能，又考查了学生的核心素养以及思维能力.一道好题就会使得一堂课丰富多彩，并激发学生的潜能，碰撞思维的火花.下面以一道椭圆试题课堂教学为例，并谈谈笔者的思考.

一、试题呈现

图1

二、求解探究

试题考查了直线与椭圆的位置关系，同时考查了逻辑推理、数学运算等数学核心素养.笔者在教学过程中发现，学生的思维很灵活，并提供了多种不同解法，使得课堂更有活力.

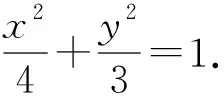
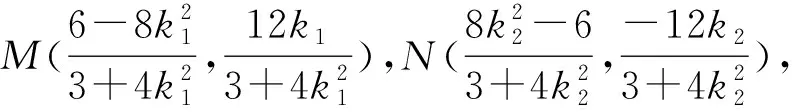
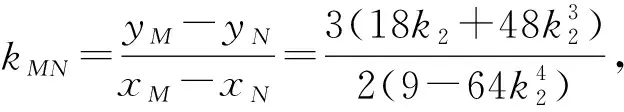
总结：在求解过程中，直线与椭圆联立，求交点、解方程、化简式子都是高中数学得基本要求.当运算遇到困难时，可以先从目标出发，中途汇合，整体代换从而高效得解决问题.可以提高学生前后兼顾得能力，培养逻辑推理、数学运算数学素养.

思考：能否不具体求出点M,N坐标，设直线l的方程，通过联立方程韦达定理刻画出点M,N的信息呢？

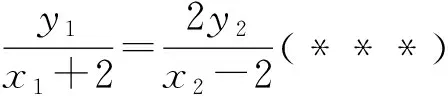
教学片断2：此时有一位同学举手并能提供更简洁得解法.

这里分析到有对称点，从而运用椭圆的几何性质，值得掌声.

教学片断3：进而探究以下问题：(3)若动直线l与椭圆交于M,N两点(直线l不过顶点且斜率存在)，记直线AM的斜率为k1，直线BN的斜率为k2，若k1=2k2，求证：直线l过定点.

由前面的解法，不难发现，此问同样采用解法4会更简单.

三、教学启示

从困境中突围，拓宽解题思路，本题得解法可谓灵活多样，最开始的思路都是通性通法，只是过程中会遇到棘手的问题，不轻易放弃，从困难中找方法，也许能擦出不一样的火花.从不同的视角、不同的高度都可以得到解决问题的思路，但不同的思路，运算的繁简程度也不尽相同，通性通法是解题的基础，要让学生独立思考、尝试解答.通过这次的教学，笔者相信学生能够站在更高的角度看待问题，培养学生的数学核心素养.