基于运算素养下的椭圆标准方程的推导*

福建省南安第一中学 (362300) 洪丽敏

数学运算是数学课堂上重要的教学活动之一，创造性的数学思维就是通过数学运算得以发展的.正如罗增儒等人在《数学教学论》中指出的：运算能力是数学教学所要培养的最基础能力，可以说只要数学存在，问题就存在，数学运算就存在.

数学运算素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，主要包括：理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等.具体而言，数学运算包括“算什么”、“如何算”、“依何算”三要素.从解决问题的角度看，知道“算什么”是第一位的，否则一切都无从谈起；从发展人的智能看，懂得“如何算”至关重要，否则会走很多弯路；从问题解决的结果看，“依何算”也是十分重要的，否则所有运算都将白忙活.

本文，笔者基于“算什么”、“如何算”、“依何算”三要素，以人教A版选修2-1中椭圆标准方程的推导为例，谈谈课堂教学中怎样落实运算素养的培养，力求“窥一斑而知全豹”.

1.算什么？

“算什么”，即要“理解运算对象”，就是要明确问题解决的对象，知道问题解决的方向.

图1

(节选)师：由上面……，我们得到平面内与两个定点F1,F2的距离之和为等于常数(大于|F1F2|)的点的轨迹为椭圆．

师：刚才好几个同学曾说“扁圆”是椭圆，那么生活中的“扁圆”一定是椭圆吗？如图1，残缺的曲线如何判断它是否属于椭圆的一部分？

生：众说纷纭.

生形成共识：需要将椭圆数量化，用数据说话.

【算什么】此时学生已明确运算对象：如何研究椭圆的标准方程.

不失一般性，可先研究焦点在x轴上的椭圆的标准方程.

2.如何算？

“如何算”，就是“厘清算的思路”，包括探究运算思路、选择运算方法、设计运算程序.

首先是设计运算程序，按照求动点轨迹方程的五步骤：建系、设点、列式、化简、说明，依次序进行.

其次是探究运算思路，具体到各个步骤，运算的具体实施.

①建系设点：如何建系能使方程更简洁？类比圆的方程，观察椭圆的几何特征，利用椭圆的对称性建系.同时为了简化运算，设焦距|F1F2|为2c(c>0)，距离之和为2a．以直线F1F2为x轴，以线段F1F2的垂直平分线为y轴，建立平面直角坐标系，则F1(-c,0)，F2(c,0)，设M(x,y)为椭圆上任意一点;

②动点M满足的条件:|MF1|+|MF2|=2a；

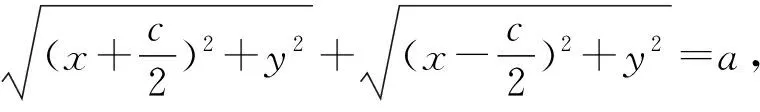
④化简：化简椭圆方程是教学难点，涉及运算方法的选择及“依何算”，两者互为渗透.

3.依何算？

“依何算”就是“明确算的依据、明白算理”，包括掌握运算法则、求得运算结果.

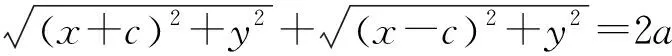
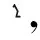
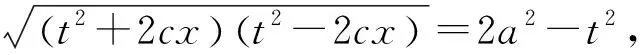
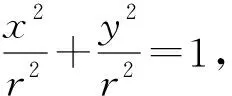
【运算思考】①为什么令a2-c2=b2，教学中不可强加给学生，可从“类比圆的方程”或从“方程的对称美”或从“优化运算”等角度加以阐述，要让学生在欣赏之中，理解“数学是合理自然的”；

②教学中，我们也可以从运算的角度对化简过程进行适度的探究，比如：

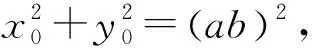
我们看到，基于运算角度对化简过程的适度探究，使得例题的呈现水到渠成.

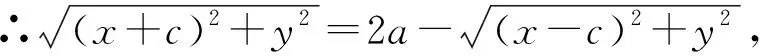
【运算思考】教材为什么要采用方案二，主要原因有二，一是这种计算思想不仅符合学生的认识水平，而且相对方案一更为优化；二是不仅保留了方案一的两种探究，而且还可以得到新的探究，比如：

可见，教材的推导方法不仅迎合学生的认知水平，而且注重培养学生的“优化意识”，还给广大的师生给予进一步拓展的空间，且与教材的例题(椭圆的其他定义和重要性质)遥相呼应.

【算理依据2】类比等差数列的性质，可构造等差数列.

【算理依据3】解析几何解题，画图是关键，可结合图形，利用平几知识求解.

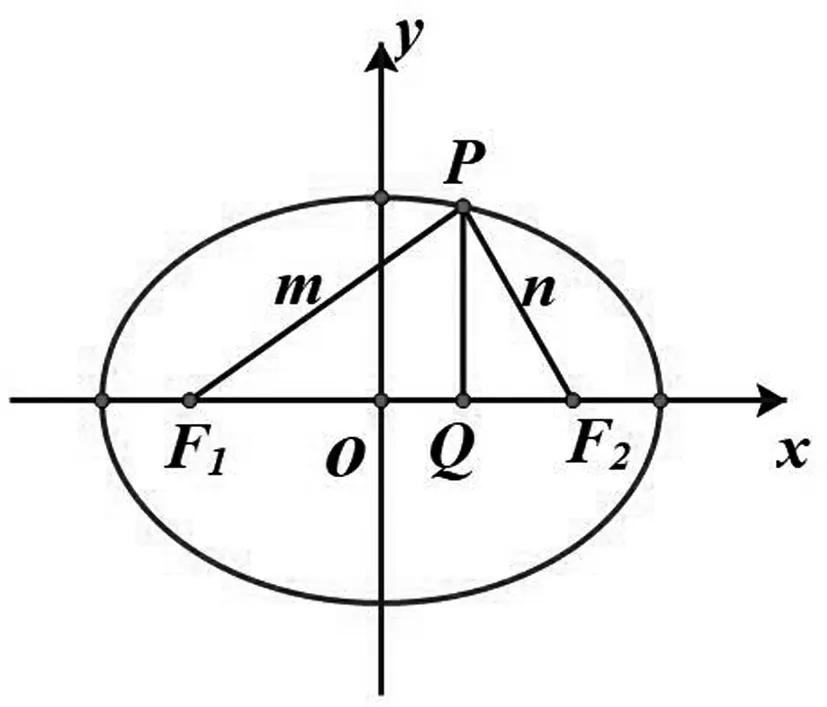
图2

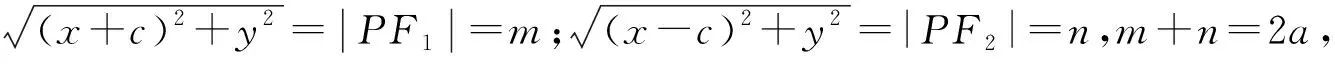
方案六：考虑△PF1F2中，|PF1|=m，|PF2|=n，|F1F2|=2c，可用余弦定理.

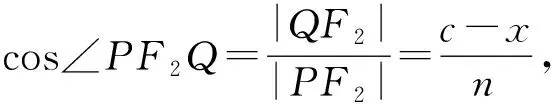
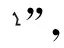
数学运算是演绎推理的重要形式，是得到数学结果的重要手段.数学运算的培养功在平时，不可急功近利.因此，教师应以课本为载体，立足课堂教学，落实数学运算的培养.特别地，“计算繁琐”常会使解析几何的教学、问题解决不尽人意.因此在解析几何教学中，教师可以不拘泥于教材的解法，从“算什么”、“如何算”、“依何算”三步骤，并可基于运算进行适度探究……让学生明白算理，合理“优化运算”，最终实现运算能力的提升.