一道高三调研题的探究及反思

江苏省连云港市外国语学校 (222006) 段丫头

解题教学是数学教学的重要组成部分,正如波利亚所说:“中学数学教学的首要任务就是加强解题训练.”因为通过解题教学,不仅可以强化学生对数学基础知识的理解和基本技能的掌握,还可以发展学生的思维能力,提高学生的数学素养.但数学教师如何才能让解题教学不落入“题海”之中?关键是教师要对选择的每一个数学问题作全面的解题研究,使每一道例题都能真正体现它的思维训练价值,使学生能举一反三、触类旁通.本文针对一道高三调研卷中的解析几何综合题第二问,谈点自己的解题体会,与同仁探讨.

一、题目再现

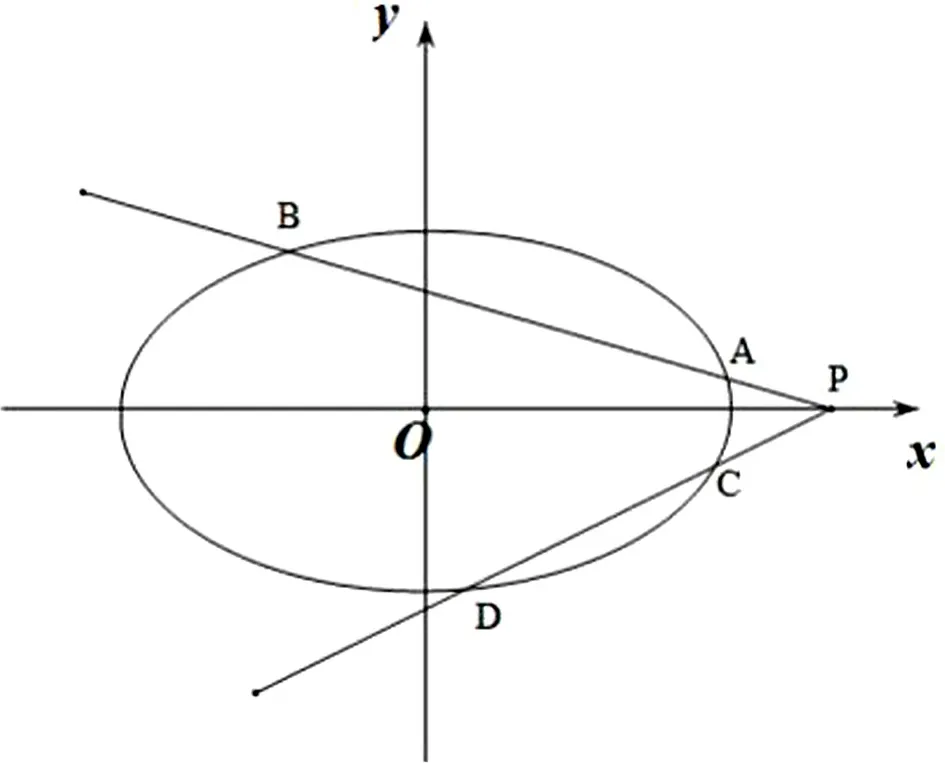
图1

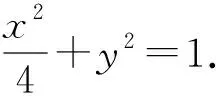
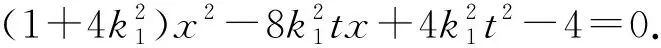
二、解题研究

1.本质寻根

在解题教学中,教师要善于引导学生分析问题,破译问题的条件和结论的内涵与外延,寻求条件与结论的关联与差异，进而认清问题的本质,建构合理的解题思路.

2.背景溯源

在解题教学中,教师不仅要能分析问题的结构,揭示问题的本质,还需要有高屋建瓴的认知能力.对于一道数学问题,不一定需要每一位学生都去弄清问题的深层次的数学背景,但身为教师却必须习惯于把握问题的源与流.教师才能游刃有余地驾驭课堂,应对课堂上那些善于钻“牛角尖”的学生的奇思妙想.实际上,本题是2018全国高中数学联赛江苏赛区复赛第二题改编而成.

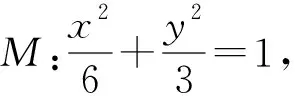
(1)证明：PA·PB=PC·PD;(2)记直线AC,BD的斜率分别为k1,k2，求证k1+k2为定值.

3.变式反思

解题教学还应使学生养成一种反思的习惯,反思可以使经验升华和理性化,产生认识上的飞跃.教师针对数学问题不仅要注意一题多解,还要注意引导学生从“变换”的思想角度去联想、拓展、纵向挖掘、横向延伸,争取做到一题多变、多题一解.这对强化数学思想方法,提高数学解题的能力都是十分有益的.

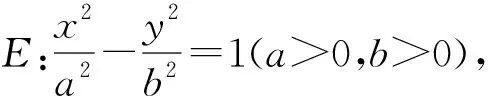
变式3 已知抛物线E：y2=2px(p>0)，过一点P(m,n)分别作直线l1和l2，直线l1和l2分别交抛物线E于点A，B和点C，D，且l1和l2的斜率分别为k1和k2，若k1+k2=0，则PA·PB=PC·PD.

4.结论应用

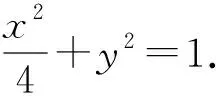
5.教学反思

解题教学中,解题并不是唯一的目的,而是一个学习与积蓄力量的过程,解题研究也不仅仅是全面的认识一道数学问题,更是对自身教研能力的一次提高.而一种良好习惯的培养,一种正确意识的确立,都会在不断的实践和熏陶中得以形成和完善.这就是提倡教师做解题研究的出发点与归宿.