一道椭圆试题的探究及变式

广东省中山市东升高级中学 (528414) 姬兴瑞

圆锥曲线一直是高中数学的主干和核心知识，特别是涉及圆锥曲线的综合解答题，由于难度和区分度较大，运算也较复杂，因而一直是高考的重头戏.本文通过探究一道与椭圆有关的定点问题，发现椭圆、双曲线、抛物线共有的一组优美结果.

一、一题多解、提炼思想

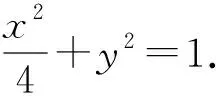
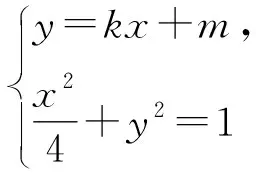
评注：此解法是解析几何试题中求定点问题的常用方法，用斜率和截距作为参数来表示直线方程，通过运算研究两个参量关系进而确定定点坐标；解法思路自然，学生容易想到，但是运算量大，对学生的运算能力有较高的要求.

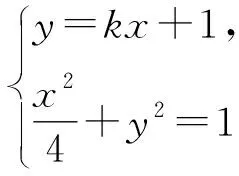
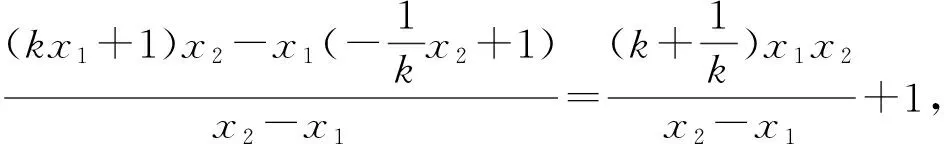
评注：本解法2根据对称关系找到定点的特殊位置，方法较为巧妙，但运算量亦较大，对学生基于图形的特征判断要求较高.

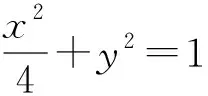
评注：本解法利用两条直线方程的乘积形式来刻画直线AB的方程，其本质是利用曲线系方程解题，可以将两条直线看做二次曲线的退化，作为曲线的特殊形式，联立两条直线(曲线)与椭圆得到的解就是对应交点A,B的坐标，从而快速锁定直线AB的方程，此过程中代数变形简单，极大提高了解题效率，但是要求学生熟悉曲线系方程的应用.

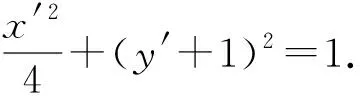
评注：解法4将两条直线的交点平移到坐标原点，使直线的斜率之积的代数形式变得简单，再联立直线和椭圆方程得到二次齐次问题，最后再根据根与系数的关系得出m,n的等量关系，进而求出定点坐标.此法大大简化运算，不失为解析几何解决定点问题的一个较好的方法.

二、一题多变，揭示本质

一题多解不是追求解题的目标，重要的是提炼解决一类问题的通性通法，揭示数学本质，形成数学方法与思想，促进学生数学抽象素养的提高.

(1)若将斜率之积-1换成任意的实数t，是否也有类似的结论？引导学生探索可得：

(2)点P(0,1)是椭圆的上顶点，自然联想到对于其他三个顶点的类似问题，通过类比探究可得到：

(3)若将椭圆方程一般化，对本题结论做拓展研究，可得如下一些一般性的结论：

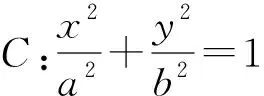
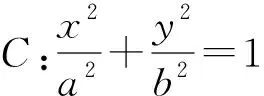
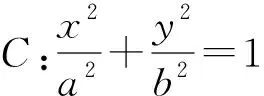
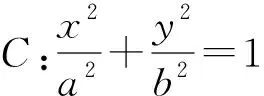
(4)若点P为椭圆C上的任一点呢？那么我们是否会有更一般的结论呢？

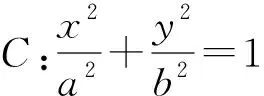
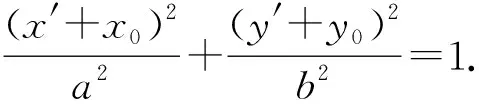
(5)由于椭圆、双曲线和抛物线都是二次曲线，可以通过类比的方式横向拓展一些结论：

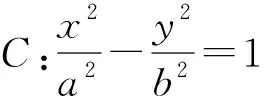
以上结论，从具体数字到字母，从特殊到一般，从椭圆到双曲线和抛物线，层层深入，不断揭示数学本质，形成一般结论.从这一道模拟试题的结论研究可知：通过对问题变条件、变结论等方式，可以引导学生对命题进行不同角度、不同层次的探究，完善了学生的认知结构和方法体系，有利于发展学生的抽象能力素养，学生数学抽象素养的形成是一个长期的过程，要求我们在平时有意识的培养和引导，只要坚持下去，学生的抽象素养能力定会大幅提升.

三、编题变式，拓展能力

显然由结论3可知，直线l过定点Q(6,0)，则P点到直线l的最大距离是PQ，即为4.

题2 已知直线y=kx+m与抛物线y2=2x交于A,B两点，且直线OA与直线OB的斜率之积为-1，其中O为坐标原点，若OM⊥AB于点M,求M点的轨迹方程.

由结论11知直线AB过定点C(2,0)，依题意得M点的轨迹是以OC为直径的圆，从而轨迹方程是(x-1)2+y2=1.

通过编题解题，一方面能加强学生对基本的解题思想方法的运用，加深学生对数学本质的理解，另一方面培养学生的创造思维能力.

四、探后反思

美国著名数学教育家波利亚说过：“掌握数学就意味着要善于解题.”而想要学会解题，好的数学题目是关键.一道好的试题之所以能引起大家的共鸣，不是因为其独特的解题技巧，而是其中蕴含着的数学思想和方法.本文中的试题素材平实，但求解方法和过程精彩纷呈，妙趣横生，真可谓是一道平中见奇的好题.在日常教学中，教师精心选择这样极具代表性的一题多解题目作为练习，通过一题多解、多题一解的训练，增强学生的数学核心素养和思维能力的提升.正如波利亚说：“一个专心的认真备课教师能拿出一个有意义的但不复杂的题目，去帮助学生发展问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的领域”.