圆锥曲线中的“圆性”探析*
2020-11-20浙江省绍兴鲁迅中学312000虞关寿
浙江省绍兴鲁迅中学 (312000) 虞关寿
先看下列两个问题:
1、已知圆O:x2+y2=r2,圆O上有一动点M在y轴上的投影为N,在x轴上有两个定点A(a,0),B(b,0),其中a≠b,b≠0,连接MA,NB相交于点P,当点M在圆上运动时,点P的轨迹是什么?
2、已知圆O的半径为定长,A是圆O所在平面上不在圆O圆周上的一定点,P是圆上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?
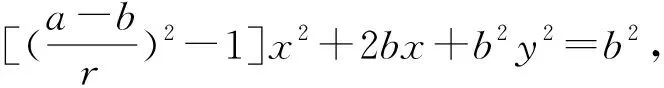
第二个问题由圆锥曲线的定义易知:当点A在圆内时,点Q的轨迹是椭圆;当点A在圆外时,点Q的轨迹是双曲线.
从上面两个问题可看出,在圆中适当调整一些条件可生成出圆锥曲线,即圆锥曲线可由圆而来.圆锥曲线的定义、有关性质及解决问题的方法策略都可“圆”化,充分体现出圆的基础性.本文从圆锥曲线的定义、几何性质、解题策略等方面探究其中的“圆性”.
一、椭圆的定义可由圆的定义来生成
我们先看圆的定义:平面有一动点M到一定点F的距离为定长a,则动点M的轨迹叫做圆.
将定点F看成是两个定点F1,F2的合点,直线段MF看成是两条线段MF1,MF2的合线段,现将两定点F1,F2拉开一段距离,设拉开的距离|F1F2|=2c,这时动点M到两定点F1,F2的距离和为|MF1|+|MF2|=2a,动点M的轨迹就成了椭圆.
椭圆就其外形来看,可以看成圆在一个外力作用下压成的.


解:(1)设动点M(x,y),两定点F1(0,-3),F2(0,3),由已知条件知MF1+MF2=10>6,得动点M的轨迹是以F1,F2为焦点,长轴长为10的一个椭圆.
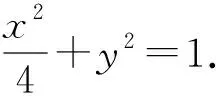
二、椭圆、双曲线、抛物线可由圆与圆的位置关系来呈现
平面内有两个定圆,这两个定圆半径不等,有一个动圆,这个动圆与这两个定圆都相切(外切或内切),则这动圆的圆心所形成的轨迹为椭圆、双曲线或抛物线.
例2 (1)已知两圆C1:(x-4)2+y2=169,C2:(x+4)2+y2=9,动圆在圆C1内部且与圆C1相内切,和圆C2相外切,则动圆圆心的轨迹方程为___;
(2)已知两圆C1:(x+3)2+y2=1,C2:(x-3)2+y2=9,一动圆与这两个定圆都外切,则动圆的圆心轨迹方程为;
(3)已知圆A:(x+2)2+y2=1与定直线l:x=1,且动圆P与圆A外切,并且与直线l相切,则动圆圆心P的轨迹方程为.
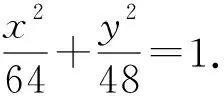
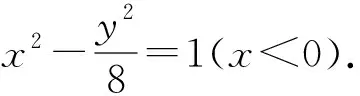
(3)设动圆圆心为P(x,y),半径为r,∵动圆P与圆A都外切,∴PA=r+1,∵动圆P与直线l相切,∴点P到直线l的距离为r.现将直线l向右平移一个单位得直线l′:x=2,则点P到直线l′的距离为r+1,即动点P到定点A的距离等于到定直线l′的距离,∴动点P的轨迹是抛物线,其轨迹方程是y2=-8x.
三、圆锥曲线的一些几何性质可由圆来体现出来
椭圆、双曲线、抛物线的几何性质常与其它元素结合来考查,如与直线、与圆等.有三个圆常常出现在各级各类的考试中,是我们值得要关注的.
1、椭圆、双曲线、抛物线的焦半径直径圆
定理1 椭圆中以焦半径为直径的圆必与长轴为直径的圆相内切;
双曲线中以焦半径为直径的圆必与实轴为直径的圆相切;
抛物线中以焦半径为直径的圆必与顶点处的切线相切.
下面以椭圆为例证之.

图1
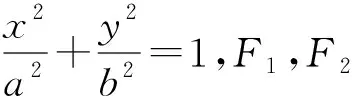
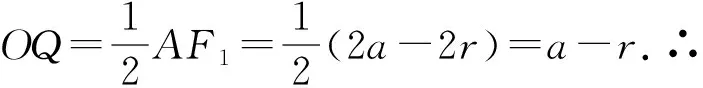
2、椭圆、双曲线、抛物线的焦点弦直径圆
定理2 椭圆中以焦点弦为直径的圆必与准线相离;双曲线中以焦点弦为直径的圆必与准线相交;抛物线中以焦点弦为直径的圆必与准线相切.
下面以抛物线为例证之.
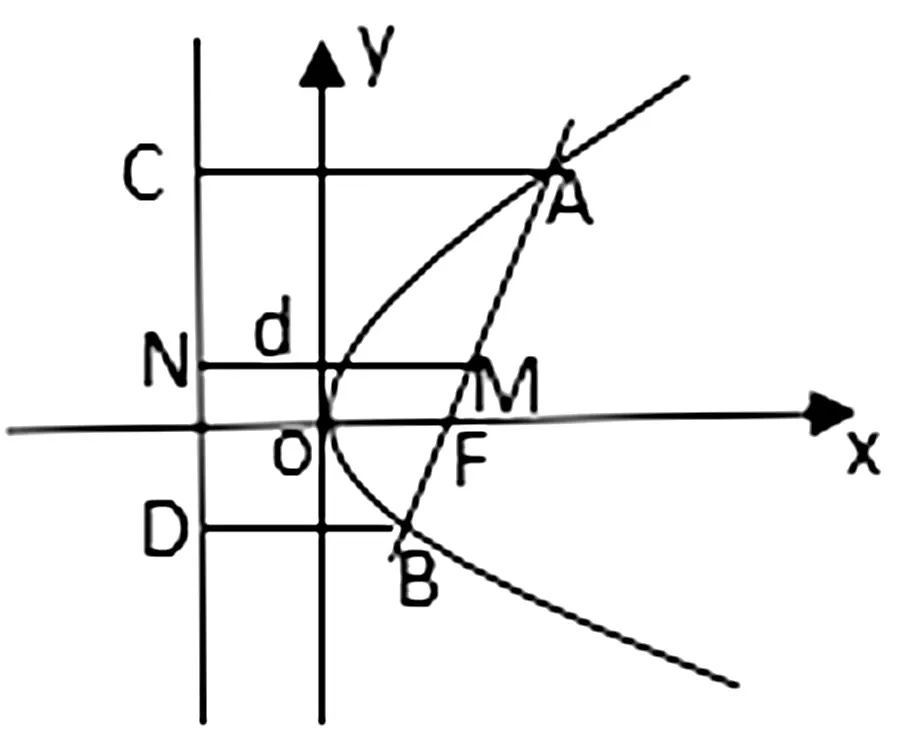
图2
例4 已知抛物线y2=2px(p>0)中,过焦点F作直线交抛物线于A,B两点,记抛物线的准线为l,以AB为直径的圆为M,如图2,求证:圆M与准线l相切.
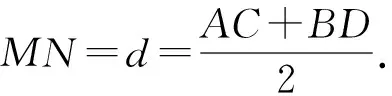
3、椭圆、双曲线、抛物线焦点三角形的内切圆
定理3椭圆中焦点三角形的内切圆圆心轨迹是以原焦点为顶点的椭圆;双曲线中焦点三角形的内切圆圆心轨迹是以过原顶点的两平行开线段(长为2b);抛物线中焦点三角形(另一焦点在无穷远处)的内切圆圆心轨迹是以原焦点为顶点的抛物线.
下面以双曲线为例证之.

图3

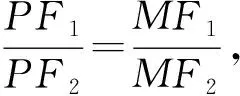
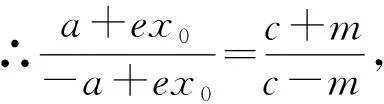
从上述证明过程中,也可得到双曲线焦点三角形的一个重要性质:双曲线焦点三角形的内切圆过定点.
四、圆锥曲线的一些综合问题可由圆辅助解决
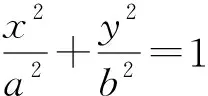
下面以椭圆为例体会解决圆锥曲线问题可借助圆的功能去完成.
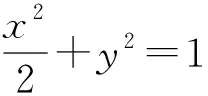
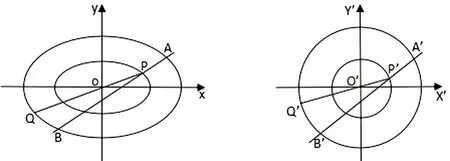
图4 图5
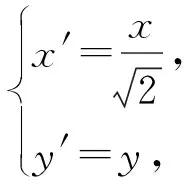


图6 图7