探“源”觅“圆” 才能“方圆”——对一道课本习题的再认识

江苏省海门中学 (226100) 顾旭东 王金忠

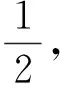
题目平易近人，可谓入手容易操作简单.也正因为大家对于书本的深耕挖掘，因此与阿波罗尼斯圆(以下简称阿氏圆)有关的题目在各省市的模拟试卷上屡见不鲜，甚至在高考中也是频频出现.笔者通过课堂研究，发现学生对于阿氏圆的由来能欣然接受，但对于其中的变用常感到心有余而力不足.鉴于此稍作整理，罗列如下，恳请各位同行和专家批评指正.

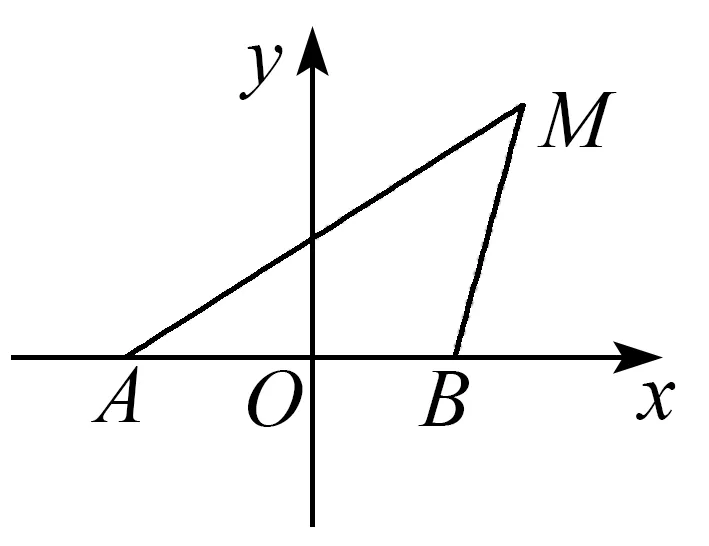
图1

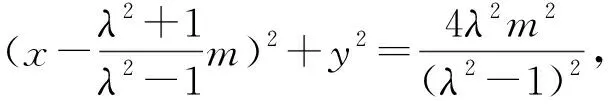
其中我们还不难发现如下结论：①该圆的圆心C与点A,B三点共线；②当λ>1时，C在射线AB上；0<λ<1时，C在射线BA上．

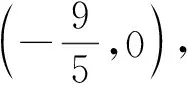
点评：本题虽说以阿圆为背景，但指向比较明确，难度一般，对普通类学生的借鉴意义不大.而对于教师来讲，实是一个不可多得素材.通过从特殊到一般的研究会发现其中定点、定值之间错综复杂的关系，我们先来看问题2.

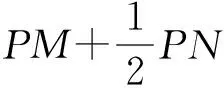
点评：本题对学生而言，困境就在于第一步，即如何利用阿圆的逆向思考来实现点的转移，无独有偶笔者发现第58届白俄罗斯数学奥林匹克竞赛的一道试题，对其中的两个点与阿氏圆中学生苦苦探寻的点不谋而合.

题目如图2，A为⊙O外一点，过点A作⊙O的割线l与⊙O交于点B,C,B′为点B关于直线OA的对称点，证明：直线OA与CB′的交点位置与直线l的选择无关.

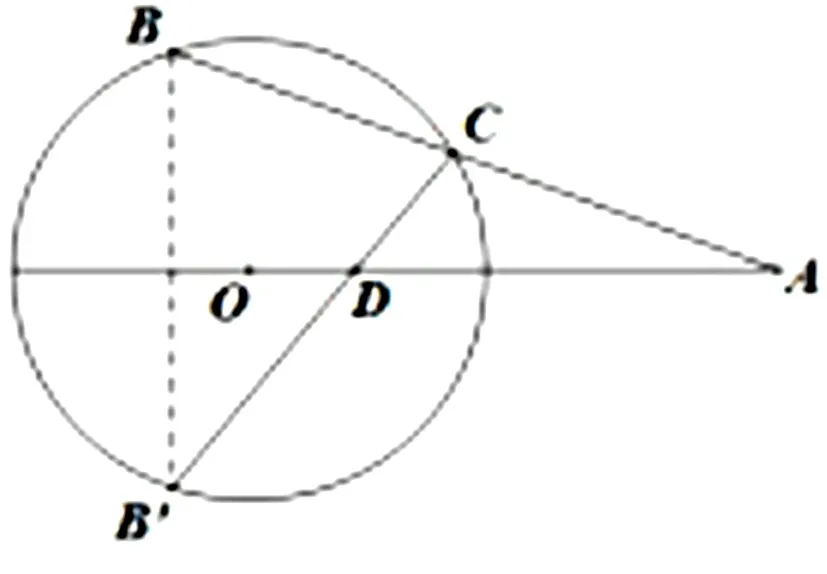
图2

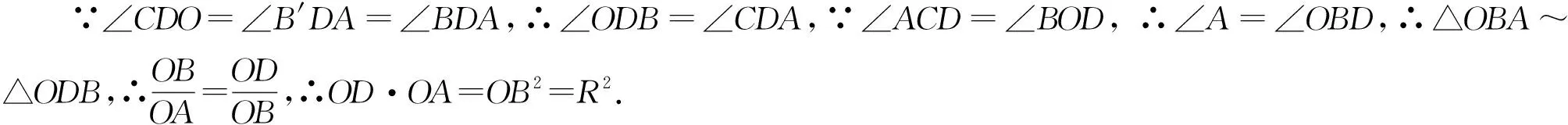
同样若通过建系(以O为原点，OA所在直线为x轴)，圆方程为x2+y2=R2,不难发现xD·xA=R2.

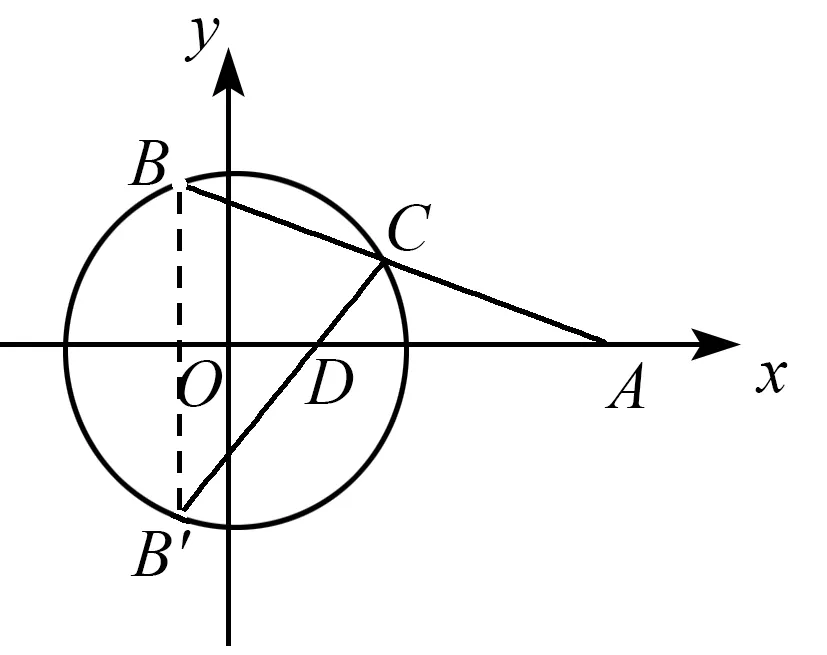
图3

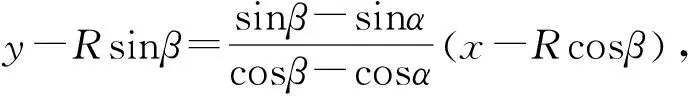
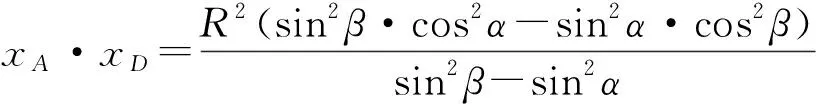
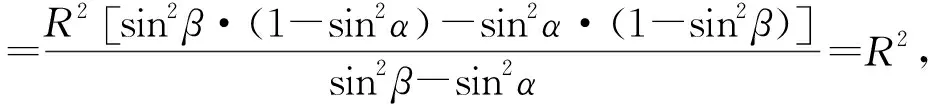
经过探索研究后，发现点A与点D不一般，若我们在圆x2+y2=R2上任取一点P(x0,y0),则

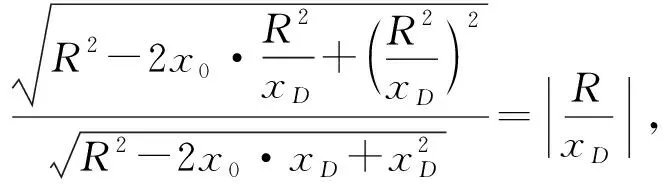
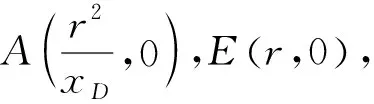
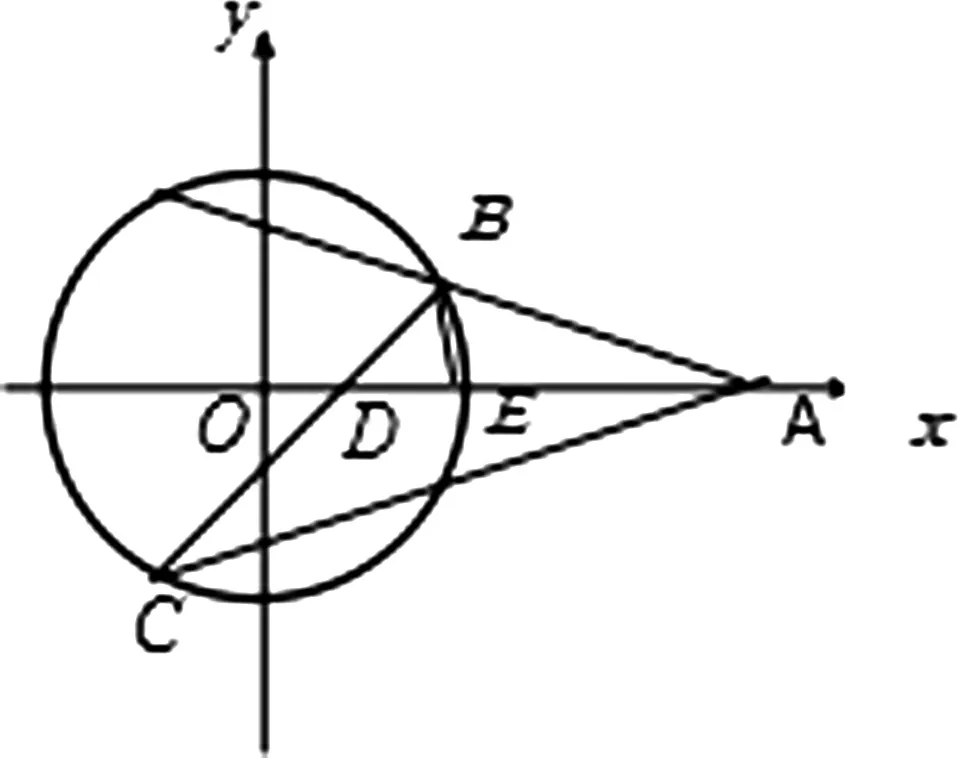
图4

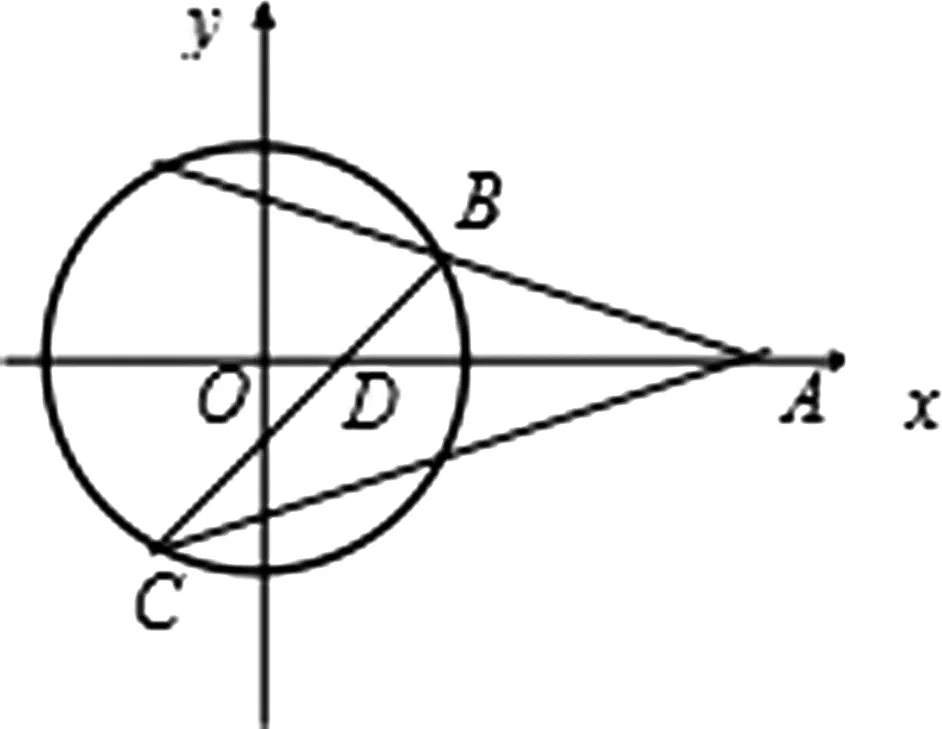
图5

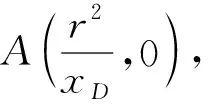
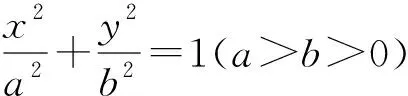
图6

同样相关的结论在双曲线与抛物线中也成立，在此不一一列出.为了表示对阿波罗尼斯的纪念，17世纪法国著名数学家费马还把以下两个关于圆的轨迹称为阿波罗尼斯轨迹.

①到n个定点的距离的平方和等于已知数的动点轨迹为圆;②动点P到两个定点A、B满足mAP2+nBP2=k2(m、n、k是正常数)，则点P的轨迹为圆.

希望通过本文的探源分析，能让学生主动体验阿圆系统化的建构过程，从而真正意义上掌握阿圆.