基于核心素养问题设计的三个原则——以利用待定系数法求多项式最值问题设计为例

浙江省宁波市北仑中学 (315800) 毛浙东

史宁中教授认为，数学教育应当遵循的一个原则是设计并且实施合理的教学活动.众所周知，问题是数学的心脏，因此在课堂教学中，教师如何设计例题就显得非常关键.不同的例题承载着不同的育人功能，教师通过合理的例题设计，进行有针对性的教学，能有效培育学生的数学核心素养.

高中阶段的数学核心素养包括六个要素，其中最为重要的有三个：抽象、推理和模型【1】.发展学生的数学核心素养，有助于学生学会用数学的语言表达世界，用数学的思维分析世界，用数学的眼光观察世界.下面笔者就以“利用待定系数法求多项式最值”这堂课为例，从核心素养的维度，来谈谈课堂中问题设计的三个原则.

1 核心素养的三个维度

1.1 维度一：用数学的语言表述问题——让学生学会建立模型

数学的语言就是数学模型，数学模型构建了数学与现实世界的桥梁，为了更好地培育学生用数学的语言表达世界的能力，教师应当在课堂中设计一些能指向数学建模能力培育的例题，培养学生举一反三的能力，完善学生知识和方法在脑海中的建构.

问题1 若x,y,z∈(0,+∞)，且4x+5y+8z=30，求8x2+15y2+48z2的最小值.

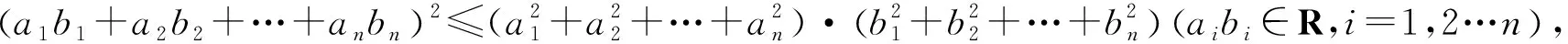
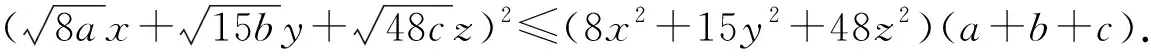
1.2 维度二：用数学的思维思考问题——让学生学会逻辑推理

用数学的思维思考问题，也就是进行逻辑推理，它体现了数学的另外一个重要的特征——严谨性.为了培育学生的逻辑推理能力，教师在进行例题设计时，需要给学生适当增加“障碍”，让学生必须先通过推理和分析，选择出最优的模型，有时甚至需要多次综合运用不同的模型，才能解决问题，这是一种更高级的要求.

问题2 已知正实数x,y,z满足x2+y2+z2=1，求xz+xy+2yz的最大值.

分析：观察题目结构，初步确定可以选择基本不等式这个模型来解决，但是对题目的数据进行仔细分析后，我们发现需要多次运用基本不等式才能顺利求解.

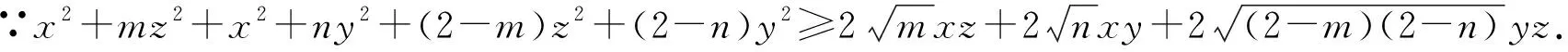
1.3 维度三：用数学的眼光看问题——让学生学会数学抽象

抽象是数学最重要的一个特征.让学生学会剥离原题的数学情境，进行数学抽象，是数学最基本的“童子功”，只有练好了这个“童子功”，我们才能学会用数学的眼光看问题，用数学的眼光洞察这大千世界.当然，在数学的抽象过程中，适当的等价转化是不可或缺的，因为这能让我们更好地看清问题的实质，从而成功地实现数学抽象.

问题3 已知函数f(x)=ax2+bx+c(a,b,c∈R)，若存在实数a∈[1,2]，对任意的x∈[1,2]，都有f(x)≤1，则7b+5c的最大值为.

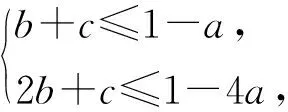
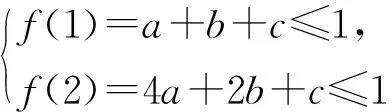
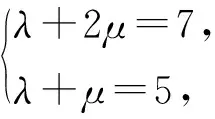
2 基于核心素养的问题链设计的三个原则

2.1 原则一:问题设计要有明确的素养指向性

基于核心素养的问题设计要有明确的核心素养培育的指向性.正所谓“有的”才能“放矢”，教师在课堂例题设计时要特别关注例题设计的目的，即关注如何通过例题教学来有效提升学生的不同数学核心素养.因为不同的问题对学生素养培育的侧重会有所不同，因此我们在设计问题时，应当先明确这堂课重点要培育学生哪方面的素养，然后根据这个目标来设计例题，让每个问题都有明确的指向性.具有明确指向性的问题设计，能有效驱动、引领学生学习，也能避免重复地、机械地在课堂中进行满堂灌，让课堂更从容，也更具有厚度和底蕴.

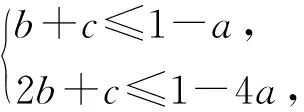
2.2 原则二:问题设计要有合理的层次梯度性

问题的设计需要遵循梯度性原则.行为主义认为，学习是刺激与反应的联结，是有机体在接受外界的刺激后做出相应的反应，是反应的强化和经验的获得，而带有梯度性的问题有助于学生可持续注意力的激发，能提升学生的学习效能.同时，这种循序渐进的做法也遵循了学生的认知规律，让学生的能力在课堂中不断螺旋上升.

比如在上述案例中，因为问题1直接利用柯西不等式的模型即可解决，是最简单的建模思想的运用，因此也是最浅层的设计，作为第一道例题是恰当的.而问题2则需要多次运用基本不等式的模型才能解决，这个过程需要一定的逻辑分析，因此问题2的层级是高于问题1的.而问题3的情境更复杂，需要先进行数学抽象，才能进行模式识别和模型建构，因为问题的难度更高，因此将其作为第三道例题.这种由浅入深，环环相扣，带有梯度性的问题设计从不同的维度培养了学生的数学核心素养.

2.3 原则三:问题设计要有紧密的内在关联性

维果茨基认为，在学生的“最近发展区”展开教学，更能加速学生的发展.具有前后关联的例题串就是在学生的近发展区中设置的一个个补给站，让学生通过不断地补充“能量”，从而能到达更远的目的地.因此具有前后关联性的例题链对学生学习的推动性是远远大于“各自为战”的例题链的.

另一个方面，虽然每一个数学核心素养都有自身的独立性，在学习数学的过程中，在发现与提出、分析与解决数学问题和实际问题中，各自在不同的环节发挥不同的作用，但我们更需要强调整体性，六个核心素养是一个有机联系的整体，它们不是两两“不交”的独立素养，而是相互“交着”相互“渗透”的【2】.既然各个核心素养本身就是相互“交着”与“渗透”的，那我们有什么理由不在问题设计时关注一下问题的前后关联性，让问题之间也能做到相互“交着”与“渗透”呢？

例如，在本案例中，我们就选择了非常“紧凑”的三个问题，围绕同一个中心和同一种方法进行设计，问题之间前后关联，你中有我，我中有你.这三个问题都围绕一个中心问题——“求多项式的最值”来展开，采用的核心方法也是一致的，都是利用待定系数法来解决，同时三个问题都渗透了数学建模的思想，它们组成了一个有机的整体.正因为问题的设计注重了其内在的关联，学生对知识和方法的理解更加深刻，核心素养的培育也更加有效.