基于动力特性的混合结构地震响应复模态叠加法

孙攀旭，杨 红,2，刘庆林3(. 重庆大学土木工程学院，重庆；重庆大学山地城镇建设与新技术教育部重点实验室，重庆；深圳信息职业技术学院交通与环境学院，深圳 5872)

由不同阻尼特性材料组成的工程结构称为混合结构，目前已经广泛应用到机械工程、航空航天工程、土木工程等领域。混合结构是非比例阻尼体系，对应的阻尼矩阵不再满足经典阻尼条件，如何求解混合结构的动力响应是抗震分析中亟待解决的问题。解决该问题的常见方法是，采用应变能法[1 − 4]、近似解耦法[5 − 6]、复频率法[7 − 8]、Rayleigh 阻尼法[9 − 11]等计算出等效阻尼比，进而基于传统的实模态叠加法计算结构动力响应。上述方法的思路是将混合结构简化为等效的单一材料比例阻尼体系，这容易导致一定的误差，计算精度难以保证。Foss[12]将运动方程扩展为状态方程组，进而提出了状态空间法。依据状态空间法，可实现混合结构的复模态叠加法，在复数域中求得运动方程的精确解[13 − 16]。复模态叠加法计算结果的正确性依赖于阻尼矩阵的合理构造，但在结构地震反应分析中，合理地构造出能正确反映结构真实情况的阻尼矩阵是十分困难的[17]。

Rayleigh 阻尼模型假定结构的阻尼矩阵是质量矩阵和刚度矩阵的线性组合[18]，由于数学处理上的简易性，使其得到了广泛的应用。Clough 等[19]将子结构的阻尼矩阵假定为Rayleigh 阻尼矩阵，进而组装得到混合结构的分块Rayleigh 阻尼矩阵。保证分块Rayleigh 阻尼模型合理性的关键在于如何确定阻尼系数。阻尼系数的计算方法不合理将带来较大误差[20 − 22]。针对如何确定Rayleigh阻尼系数的问题，国内外学者进行了系统研究，Idriss 等[23]仅采用结构的基本频率确定阻尼系数，Yoshida 等[24]提出了在主要频率范围内计算阻尼系数的方法，Hudson 等[25]依据结构的基本频率和地震波的卓越频率确定阻尼系数，邹德高等[26]、李哲等[27]在考虑结构基本频率和地震波卓越频率的基础上，进一步修正了阻尼系数的计算方法，许紫刚等[28]提出基于基本频率、地震波卓越频率与形心频率的平均值确定阻尼系数。为考虑整个振动频率范围内阻尼系数的影响，王田友等[29]依据结构的基本频率和输入振动的频率范围确定两个振型，并用于计算阻尼系数，潘旦光等[30 − 32]以结构位移反应峰值的误差为目标函数，采用最小二乘法确定阻尼系数。

上述方法依据结构体系的振动特性和/或外激励的频谱特性确定阻尼系数，本文在上述研究的基础上，提出了基于结构动力响应特性确定阻尼系数的新思路。Rayleigh 阻尼系数一般通过选择两个重要振型的自振频率和振型阻尼比进行确定，为保持这一工程常用方法的简便性，同时解决振型选择方式不唯一导致地震响应计算结果存在不确定性的问题，本文提出了一种基于动力特性确定Rayleigh 阻尼系数的计算方法，即在求解瞬态反应时，根据结构的前两阶振型确定阻尼系数；求解稳态反应时，根据结构的基本振型和外激励频率确定阻尼系数，可有效避免传统方法计算阻尼系数时振型选择的不唯一性，从而构建出对应的分块Rayleigh 阻尼矩阵，实现了混合结构的复模态叠加法。事实上，非比例阻尼模型计算过程需涉及复振型，这样才能更符合工程问题的本质特性[33]，相比基于等效阻尼比的实模态叠加法，本文提出的基于动力特性的混合结构地震响应复模态叠加法可考虑工程结构中不同阻尼特性材料导致的非比例阻尼特性。

1 基于动力特性的阻尼矩阵构建

1.1 黏性阻尼模型的复模态叠加法

基于黏性阻尼模型的时域运动方程为：

式中：M为质量矩阵；K为刚度矩阵；I为与地震动输入有关的向量(N×1 )，与g(t)方向相同的位移自由度元素为1。

由M和K可计算得到结构的无阻尼自振频率，进一步依据分块Rayleigh 阻尼模型[19]，阻尼矩阵可表示为：

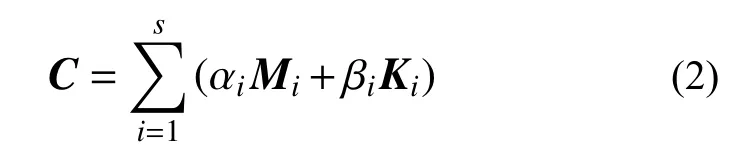
1.2 基于动力特性的阻尼矩阵构造

混合结构复模态叠加法的正确性依赖于合理的阻尼矩阵，目前常用的阻尼矩阵构造方法为分块Rayleigh 阻尼模型。Rayleigh 阻尼模型的实质是选择两个重要的振型，以便使计算的结构动力响应逼近结构的实际响应。结构承受地面运动激励时需要考虑瞬态反应和稳态反应[19]，因此本文依据瞬态反应和稳态反应的特性分别确定对结构动力响应贡献最大的两个振型，进而构建出阻尼矩阵。

考虑到地震波可以分解为一系列简谐波，因此首先分析谐波作用下基于黏性阻尼模型的时域运动方程，对应的方程形式为：

随着振型阶数的增加，ωj逐渐增大，振幅的幅值H逐渐减小，qpj(t)逐渐减小，同时振型参与系数 γj也逐渐减小；当阻尼比 ξj较小， 2ξjβj的大小可忽略不计， βj接近1 时，振幅的幅值趋近于无穷大，此时结构发生共振现象。因此，在结构的稳态反应xp(t)中，最重要的两阶振型分别为第一阶振型以及与外激励频率接近的振型。

综上，本文提出了基于结构线弹性响应分离的经典思路构造分块Rayleigh 阻尼矩阵的新方法，即针对瞬态反应部分，选择与第一阶振型和第二阶振型对应的自振频率、振型阻尼比构造分块Rayleigh 阻尼矩阵；针对稳态反应部分，选择第一阶振型以及与外激励频率接近振型所对应的自振频率、振型阻尼比构造分块Rayleigh 阻尼矩阵。

2 基于地震波卓越频率的混合结构复模态叠加法

2.1 基于地震波卓越频率的阻尼矩阵

地震波作用下基于分块Rayleigh 阻尼矩阵模型的齐次运动方程为：

依据1.2 节分析，求解齐次方程通解时，选取第一阶振型和第二阶振型对应的自振频率和振型阻尼比，可计算出阻尼系数为：

式中：ω1为第一阶振型的自振频率；ω2为第二阶振型的自振频率； ξei为第i种材料对应子结构的材料阻尼系数产生的振型阻尼比[9, 34 − 35]。

地震波作用下基于分块Rayleigh 阻尼矩阵的非齐次运动方程为：

稳态反应对应的阻尼矩阵可表示为：

依据1.2 节分析，求解非齐次方程特解时，选择第一阶振型、与外激励频率接近振型对应的自振频率和振型阻尼比。目前确定阻尼系数的计算方法较多[23 − 32]，本文对比了利用结构基频确定阻尼系数的方法、利用最小二乘法确定阻尼系数的方法、利用结构基频和地震波卓越频率确定阻尼系数的方法。选择不同的方法并不影响以下理论推导过程，为了更清楚地展示本文方法的核心思路、保持计算的简便性，并考虑同时利用结构振动特性和地震动特性，本文首先选择依据结构的第一阶振型自振频率、地震波卓越频率确定阻尼系数，进一步可得：

综上，由式(35)可确定阻尼系数，进而得到了基于地震波卓越频率的分块Rayleigh 阻尼矩阵。

2.2 基于地震波卓越频率的复模态叠加法

采用数值积分方法进行计算时，按照时间步长 ∆t对输入地震动加速度记录进行离散，任意时刻可表示为tk=k∆t(k=0,1,2,···) ，利用tk时刻结构的动力响应，计算tk+1时刻的响应。由式(16)可知，求解混合结构的加速度响应需要计算方程式(14)中单自由度结构的加加速度(即qj(t)的三阶微分)，因此传统的时域逐步积分计算方法将不再适用，本文采用瞬态反应与稳态反应分离的时域数值方法计算结构的动力响应。

重复式(36)～式(45)，可实现基于地震波卓越频率的混合结构复模态叠加法。

3 基于地震波的谐波频率的混合结构复模态叠加法

3.1 基于谐波频率的阻尼矩阵

对于频带较宽的地震波，卓越频率不能有效地表现地震波的主要频谱特性，为此本文对基于地震波卓越频率的阻尼矩阵进行改进，将输入地震波加速度采用三角级数展开，得：

综上，由式(51)可确定阻尼系数，进而得到基于谐波频率的分块Rayleigh 阻尼矩阵。

3.2 基于谐波频率的复模态叠加法

为实现基于谐波频率的复模态叠加法，首先计算齐次运动方程对应的通解xc(t)，与基于地震波卓越频率的复模态叠加法相同，解耦后的齐次方程为式(36)，求解可得：

依据复特征向量的正交性，可由xc(t0) 和x˙c(t0)得到qcj(t0) 和q˙cj(t0)，完成初值的确定，进而实现基于谐波频率的混合结构复模态叠加法。

4 试验校核与计算分析

图1 试件动力响应的试验系统Fig. 1 Test system of specimens’ dynamic responses

将由不同阻尼特性材料组成的悬臂板试件作为试验对象采用图1 所示的试验测试系统，通过振动台控制系统对试件的基底施加随机激励，同时采用多普勒振动测试系统测量试件的动力响应。振动测试系统可直接采集试件的速度响应，需根据采集频率进行相应的积分或微分处理才能得到构件的位移或加速度响应，为避免后期的数据再处理导致的误差，本文仅分析了试件的速度响应，以验证本文方法的正确性。

悬臂板试件的具体尺寸如图2 所示，拾振点的位置如图3 所示，考虑到4 个拾振点的位置是对称分布的，本文仅选取拾振点A和拾振点B的动力响应进行分析、对比。试验选取尺寸和材料相同的2 个试件(CP-1 和CP-2)进行测试，试件的材料参数如表1 所示，子结构的振型阻尼比为对应材料损耗因子的1/2[38−40]，基层结构的振型阻尼比为0.0015，阻尼层结构的振型阻尼比为0.295。采用数值模拟，由试件的整体质量矩阵和整体刚度矩阵通过模态分析可得到试件的前5 阶振型的无阻尼自振频率为15.26 Hz、35.58 Hz、90.13 Hz、118.54 Hz 和132.41 Hz。

图2 试件的尺寸 /mm Fig. 2 Size of specimen

图3 拾振点的位置 /mm Fig. 3 Locations of vibration receiving points

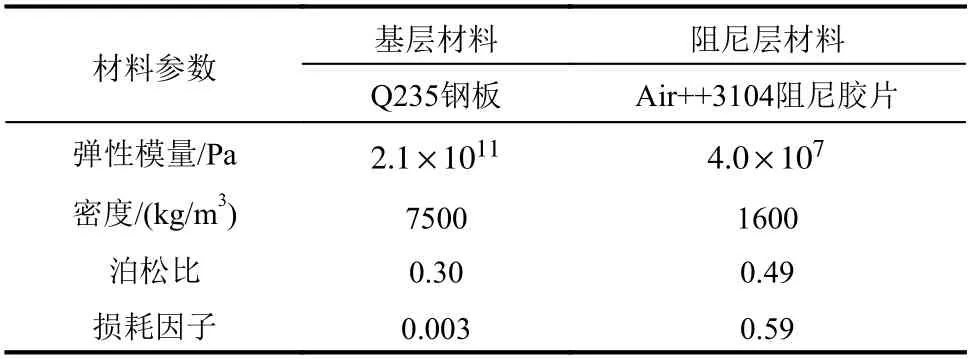
表1 试件的材料参数Table 1 Material parameters of specimen

4.1 试件CP-1 的试验结果和计算结果对比

利用振动台控制系统，对试件CP-1 施加随机激励，其振动频率的范围为100 Hz～150 Hz。由信号采集系统可得到随机激励的加速度时程(见图4(a))和对应的傅里叶谱(见图4(b))。分别采用基于第一阶振型和第二阶振型的复模态叠加法(CRS)、本文提出的基于地震波卓越频率的复模态叠加法(CRZ)和基于地震波的谐波频率的复模态叠加法(CRX)计算试件CP-1 在随机激励作用下的速度时程，并将其分别与多普勒振动测试系统测量的试件速度响应时程(CP-1-Test)进行对比，结果如图5 所示。如表2 所示，对比拾振点A的速度峰值IA，CRS的相对误差 δA为39.33%，CRZ 的相对误差 δA为10.49%，CRX 的相对误差 δA为8.16%；对比拾振点B的速度峰值IB，CRS 的相对误差 δB为32.19%，CRZ 的相对误差 δB为15.78%，CRX 的相对误差δB为11.90%。结果表明，相比CRS，考虑了地震动频谱特征影响的CRZ 和CRX 的计算精度更高；对于窄频带的外激励，相比CRZ，CRX 的计算精度并没有明显提高，但CRX 的计算量较大。因此，对于窄频带的外激励，应优先选用CRZ。

4.2 试件CP-2 的试验结果和计算结果对比

利用振动台控制系统对试件CP-2 施加频带较宽的随机激励，其振动频率的范围为40 Hz～150 Hz。由信号采集系统可得到随机激励的加速度时程(见图6(a))和对应的傅里叶谱(见图6(b))。分别采用CRS、CRZ 和CRX 计算试件CP-2 在随机激励作用下的速度时程，并分别与多普勒振动测试系统得到的速度时程(CP-2-Test)进行对比，结果如图7所示。如表3 所示，对比拾振点A的速度峰值IA，CRS 的相对误差 δA为23.45%，CRZ 的相对误差 δA为13.11%，CRX 的相对误差 δA为7.92%；对比拾振点B的速度峰值IB，CRS 的相对误差 δB为47.50%，CRZ 的相对误差 δB为19.28%，CRX 的相对误差 δB为11.15%。结果表明，与试件CP-1 的分析结果相同，CRZ 和CRX 的计算精度相比CRS 明显更高。与试件CP-1 不同的是，随着外激励频带增宽，CRX 的计算精度比CRZ 明显增高。因此，CRZ 计算量更小、适用范围受限，CRX 的计算精度更高，具有更宽泛的适用范围，在对计算精度有要求时，建议采用CRX。

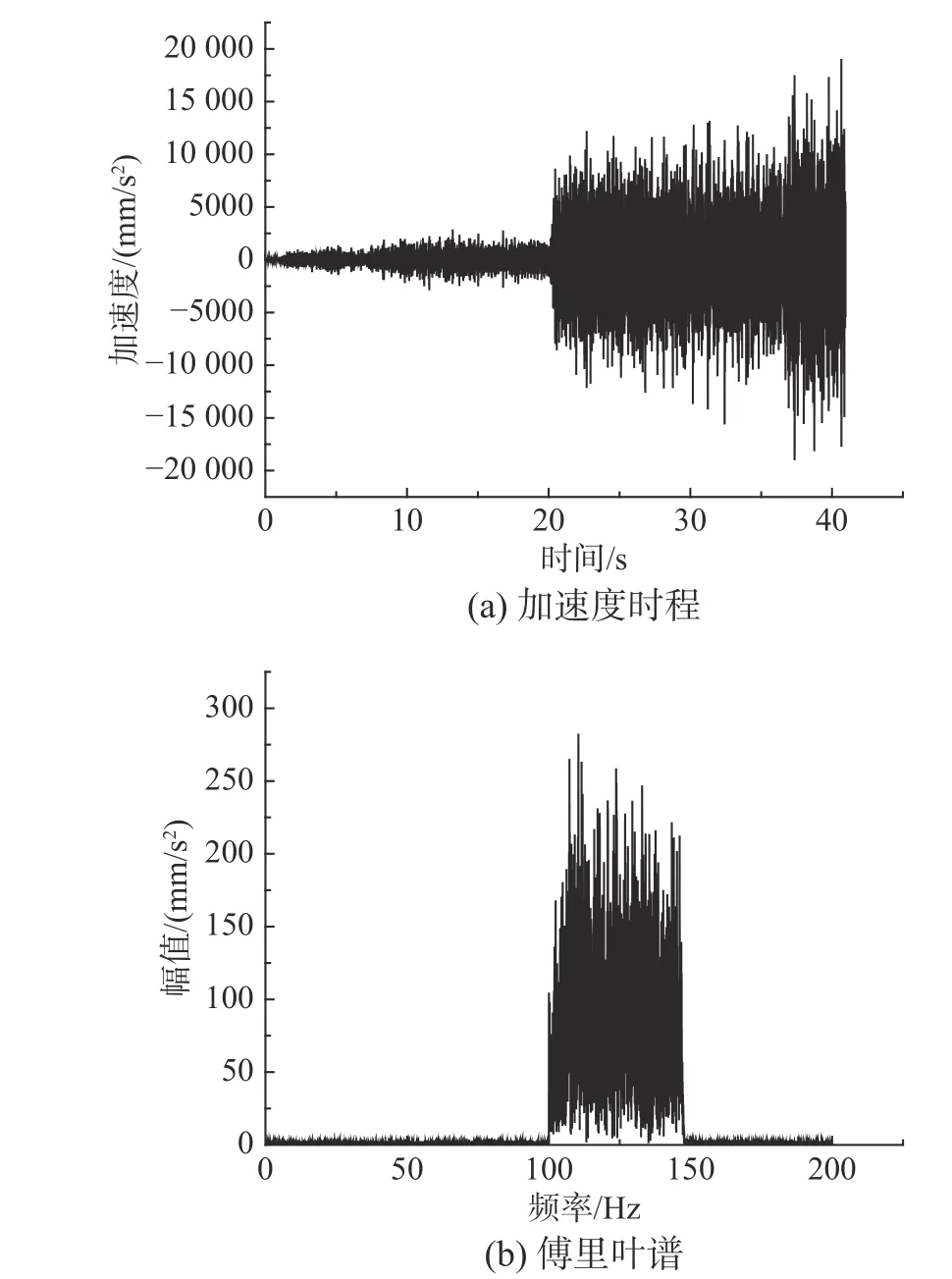
图4 试件CP-1 的随机激励Fig. 4 Random external excitation of specimen CP-1

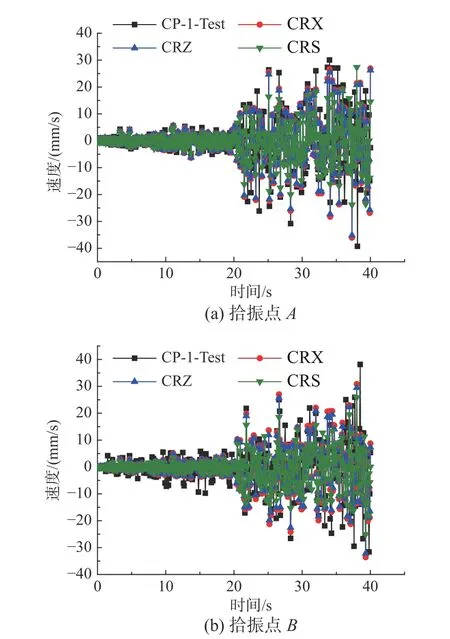
图5 试件CP-1 的速度响应时程Fig. 5 Velocity time-history responses of specimen CP-1

5 算例分析

如图8 所示，模型A 和模型B 是由不同阻尼特性材料组成的7 层平面框架，1 层～4 层均为钢筋混凝土结构、5 层～7 层为钢结构。框架底层高度皆为6 m、其余各层层高均为3 m，跨度均为6 m，钢筋混凝土柱、梁的截面尺寸分别为400 mm×500 mm、300 mm×400 mm，钢柱、梁的截面尺寸分别为HM400 mm×300 mm×10 mm×16 mm、HM300 mm×200 mm×8 mm×12 mm，各 楼 层 集 中 质 量 皆 为2 0000 kg。与模型A 相比，模型B 的唯一区别是增设了X 型阻尼器，材料参数见表4。

表2 试件CP-1 的动力响应对比Table 2 Comparisons of dynamic responses of specimen CP-1

图6 试件CP-2 的随机激励Fig. 6 Random external excitation of specimen CP-2

图7 试件CP-2 的速度响应时程Fig. 7 Velocity time-history responses of specimen CP-2

表3 试件CP-2 的动力响应对比Table 3 Comparisons of dynamic responses of specimen CP-2

地震动输入选取天津地震波和迁安地震波，对应的加速度时程和傅里叶幅值谱分别如图9 和图10 所示。其中，天津地震波的频带较窄，迁安地震波的频带较宽。分别采用基于应变能法的实模态叠加法(RY)[1 − 4]、CRZ 和CRX 计算模型A、模型B 在地震波作用下结构顶层节点1(位置见图8)的动力响应，结果如图11、图12、图13 和图14所示。

图8 模型示意图Fig. 8 Schematics of structural models

表4 不同材料的参数Table 4 Parameters of different materials

对于模型A，天津地震波作用下，RY、CRZ和CRX 计算得到的顶层动力响应时程近似相等(见图11)。相比RY，CRZ 的位移峰值相对误差为3.65%，加速度峰值相对误差为2.47%；CRX的位移峰值相对误差为0.35%，加速度峰值相对误差为在0.30%(见表5)。迁安地震波作用下，RY和CRX 计算得到的顶层加速度时程近似相等，但CRZ 计算得到的动力响应时程明显不同(见图12)。相比RY，CRZ 的位移峰值相对误差为19.78%，加速度峰值相对误差为14.96%；CRX 的位移峰值相对误差为0.27%，加速度峰值相对误差为在0.18%(见表5)。因此，对于非比例阻尼特性较小的混合结构，RY 和CRX 的计算结果近似相等，而CRZ 仅适用于计算窄频带地震波作用下结构动力响应。

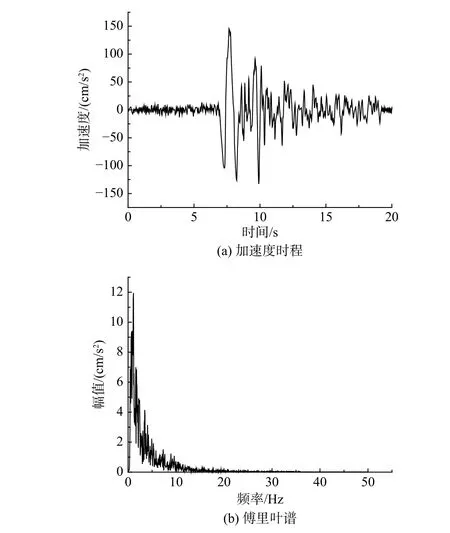
图9 天津地震波的加速度时程和傅里叶谱Fig. 9 Acceleration time-history and Fourier amplitude spectrum of Tianjin seismic wave

图10 迁安地震波的加速度时程和傅里叶谱Fig. 10 Acceleration time-history and Fourier amplitude spectrum of Qian'an seismic wave

图11 天津波作用下模型A 的顶层时程响应Fig. 11 Top floor time-history responses of Model A under Tianjin wave

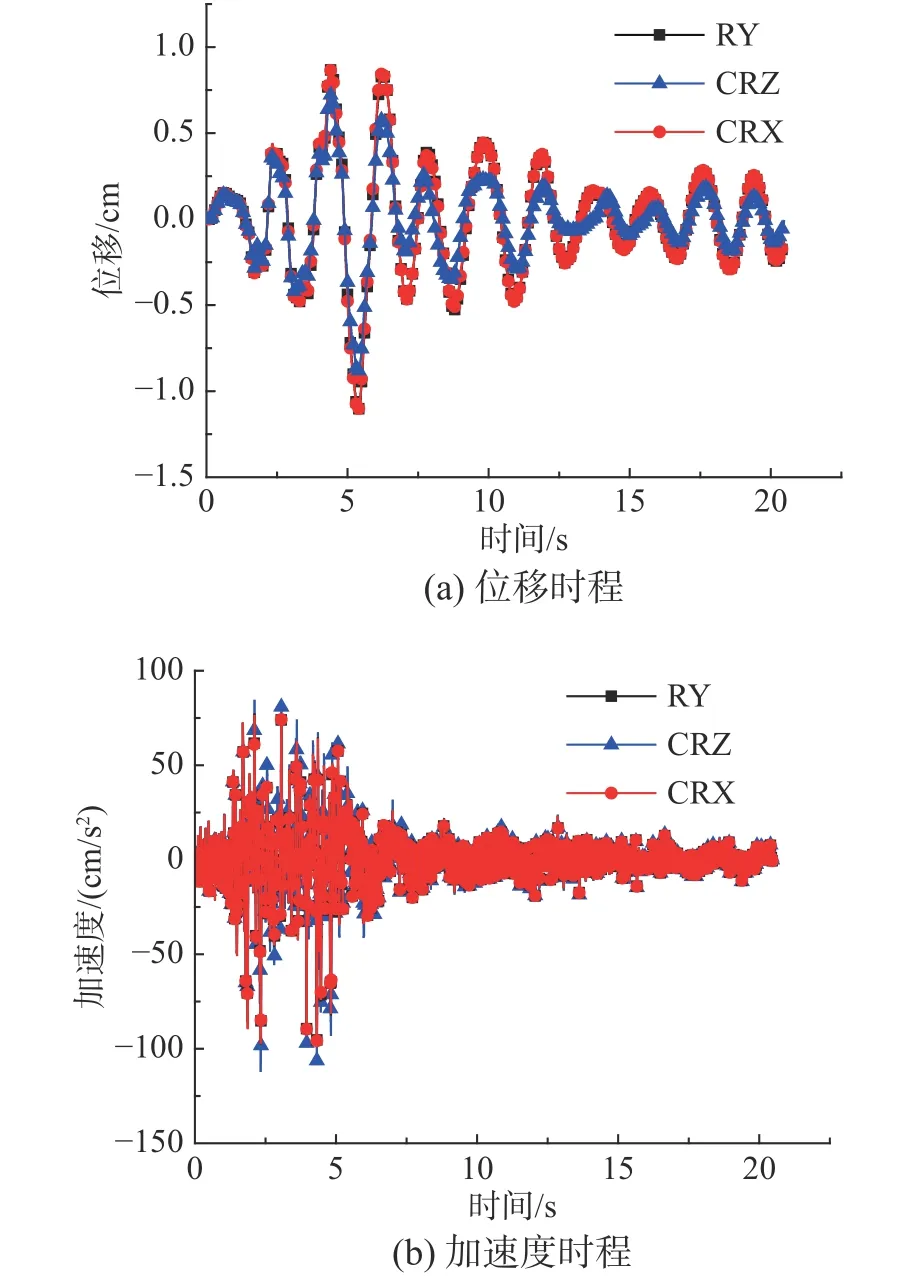
图12 迁安波作用下模型A 的顶层时程响应Fig. 12 Top floor time-history responses of Model A under Qian'an wave

图13 天津波作用下模型B 的顶层时程响应Fig. 13 Top floor time-history responses of Model B under Tianjin wave

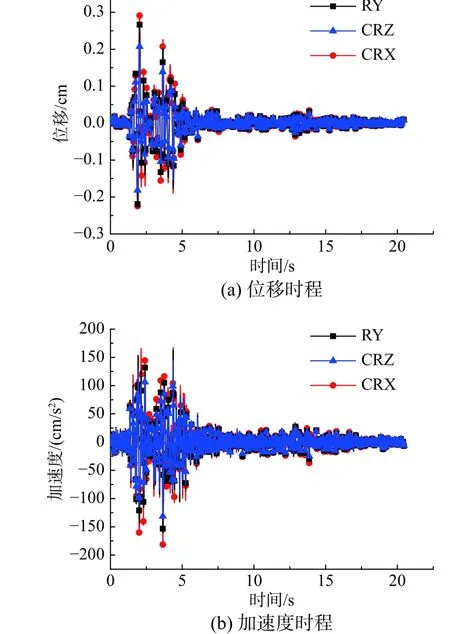
图14 迁安波作用下模型B 的顶层时程响应Fig. 14 Top floor time-history responses of Model B under Qian'an wave

表5 模型A 的顶层响应对比Table 5 Comparisons of top floor responses of Model A

对于模型B，天津地震波作用下，CRZ 和CRX计算得到的顶层动力响应时程近似相等，RY 计算得到的动力响应时程明显不同(见图13)。相比RY，CRZ 的位移峰值相对误差为12.85%，加速度峰值相对误差为22.11%；CRX 的位移峰值相对误差为10.19%，加速度峰值相对误差为在17.16%(见表6)。迁安地震波作用下，RY、CRZ 和CRX计算得到的模型B 顶层加速度时程明显不同(见图14)。相比RY，CRZ 的位移峰值相对误差为22.21%，加速度峰值相对误差为11.58%；CRX 的位移峰值相对误差为12.12%，加速度峰值相对误差为在11.98%(见表6)。因此，对于非比例阻尼特性较大的混合结构，RY 与CRZ、CRX 的计算结果差异较大。与模型A 的规律相同，窄频带地震波作用下，CRZ 和CRX 的计算结果近似相等，随着地震波频带的增宽，CRZ 与CRX 的计算结果差异增大。

表6 模型B 的顶层响应对比Table 6 Comparisons of top floor responses of Model B

综上，对于非比例阻尼特性较小的混合结构，RY 与CRZ、CRX 的计算结果近似相等，随着混合结构非比例阻尼特性增大，RY 与CRZ、CRX 的计算结果差异增大。与试验结果的规律相同，CRZ 的计算量小，但仅适用于窄频带地震波作用下结构动力响应的计算；CRX 的计算精度更高，且适用于宽频带地震波作用下结构动力响应的计算，但计算量大。

6 结论

针对基于Rayleigh 阻尼模型的地震反应分析过程中阻尼系数确定方法存在的问题，本文提出了基于动力特性确定Rayleigh 阻尼系数的新方法，经过理论推导和试验校核得到以下结论：

(1)求解地震波作用下结构的瞬态反应时，依据结构的前两阶振型确定阻尼系数；求解地震波作用下结构的稳态反应时，依据结构的基本振型、与地震波卓越频率接近的振型确定阻尼系数，得到基于地震波卓越频率的分块Rayleigh 阻尼模型。结合输入地震波加速度时程在时间步长内线性变化的假定，提出了相应的混合结构复模态叠加法。

(2)卓越频率仅能反映窄频带地震波的频谱特性。对于具有明显宽带频谱特性的地震波，借助快速傅里叶变换，将输入地震波加速度表示为一系列谐波的叠加组合，得到每一条谐波的频率。求解地震波作用下结构的稳态反应时，依据结构的基本振型、与谐波频率接近的振型确定阻尼系数，得到基于谐波频率的分块Rayleigh 阻尼模型，建立了对应的混合结构复模态叠加法。

(3)试验结果和计算对比分析表明，基于动力响应特性确定Rayleigh 阻尼系数的计算方法避免了传统方法存在的振型选择不唯一导致的计算结果不确定的问题，且计算结果误差较小；与基于地震波卓越频率的复模态叠加法相比，基于谐波频率的复模态叠加法计算量更大，但计算精度更高、适用范围更广。