基于ACP的碳纤维复合材料气瓶渐进损伤与爆破压力预测

窦丹阳 郑传祥 林 娇 陈建阳

（浙江大学化工机械研究所）

复合材料碳纤维增强气瓶有许多优点，被广泛应用在航空航天、化学工程、车辆工业及生物工程等领域［1］。现今，复合材料气瓶技术发展呈现出越来越多样化的趋势，这也和我国经济快速增长的国情密切相关。 随着人口总量和工业生产的不断增长，能源供需短缺和环境保护问题亟需改善。 碳纤维复合材料气瓶是国家“十三五”规划部署在新材料领域的项目，其科学研究领域众多。

复合材料气瓶爆破失效主要是由纤维失效引起的连锁反应，在出现初次失效点后，失效处纤维刚度软化， 应力在其他纤维层重新分配，致使新的纤维层发生失效，直到结构失效。 因此，气瓶的极限强度是衡量一个气瓶质量优劣的重要指标。 但由于各项异性的材料的复杂力学特性，至今还不能用完全准确的方法预测。

陈营利用APDL对复合材料气瓶自紧和残余预应力影响进行了探究［2］。 Wu Q G等利用Hashin失效准则模拟气瓶渐进失效，发现自紧力对气瓶平均应力有显著影响［3］。 施建伟利用ABAQUS基于连续介质损伤力学模型对复合材料层合板失效过程力学变化进行了分析［4］。 王宗鑫和赵建平利用ABAQUS研究处于不同工况的气瓶等效塑性应变值，得出承载的压力小于自紧力时该值相等的结论［5］。 Ramos I等利用ANSYS APDL通过Tsai-Wu破坏准则评估了复合压力容器失效条件，并预测了爆破压力［6］。 王浩利用ACP分别以最大应变/应力准则对有缺陷复合材料气瓶极限承载力进行了探究［7］。

复合材料建模软件ACP （ANSYS Composite Pre/Post）是整合于ANSYS Workbench环境的新的复合材料前后处理模块。 ACP的可视化铺层信息定义、支持定义复杂的纤维铺层形状，与复合材料气瓶制作工艺相同的人性化建模方式，在处理层压复合材料结构方面具有非常高的优势。

目前，工程上普遍使用APDL或ABAQUS模拟气瓶受力，采用最大应力准则或最大应变准则预测， 但这种方法有以下问题：APDL或ABAQUS和ACP相比不能进行直观的铺层设置， 在复杂铺层要求下，尤其是封头处纤维缠绕角度和厚度不断变化时，需要多级分段设置，不够准确且较为繁琐；采用最大应力准则或最大应变准则预测没能考虑纤维渐进失效这一真实过程。

笔者以长为493.2mm， 公称容积为2.4L的钢结构内胆碳纤维复合材料气瓶为研究对象，采用Hashin失效准则对它在ACP中进行渐进失效仿真模拟， 重点分析气瓶内胆和纤维缠绕层筒体、封头处的应力分布和大小，预测气瓶最终的失效压力。

1 模型建立

1.1 几何模型

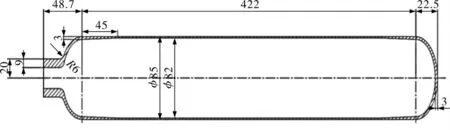
图1 2.4L气瓶几何结构

1.2 材料属性

复合气瓶的材料属性定义分为两部分：内衬和复合材料层。

文中复合材料气瓶的内衬采用6061-T6铝合金材料，纤维采用碳纤维T800，材料的室温性能参数见表1。

表1 铝合金与碳纤维的力学性能参数

气瓶的纤维缠绕层力学性能见表2，其中E为不同方向的弹性模量，下标x为纤维方向，y、z为垂直于纤维方向。 Prxy代表xy平面的泊松比，指的是在单轴作用下，x方向的单位拉（或压）应变所引起的y方向的压（或拉）应变，同理Prxz和Pryz代表xz和yz平面的泊松比。Gxy、Gyz、Gxz分别代表xy、yz和xz平面的剪切模量， 第1个下标代表作用面的外法线方向，第2个下标代表应力分量。

表2 碳纤维/环氧树脂复合材料力学性能

1.3 有限元模型建立和网格划分

如图2所示将实体模型导入Spaceclaim即可抽取实体外表面模型，将上述两个模型分别导入Static Mechanical和ACP-Pre中。

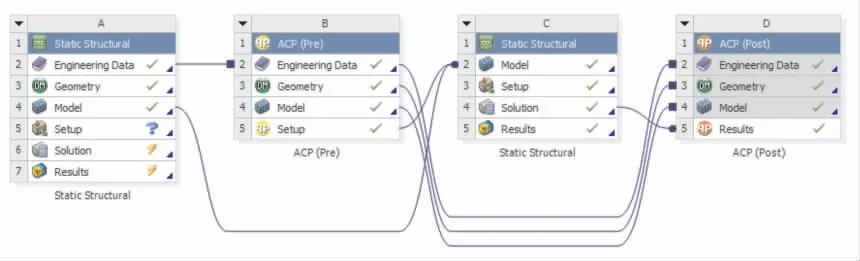
图2 ACP有限元分析流程软件界面

对封头与气瓶口过渡处附近的网格进行了细化。 一方面是由于此处几何形状变化较大，应力分布较复杂；另一方面是由于纤维缠绕在这里切根， 所以缠绕层的厚度在这里有很大的变化，网格细化能比较好地模拟缠绕层在该位置的分布情况。

ANSYS Workbench中实体的单元类型是10节点的四面体单元（Solid187）和20节点的六面体单元（Solid186），壳体的单元类型是4节点的四边形单元（Shell181），笔者选用Solid186和Shell181分别对内衬和纤维层划分网格。

对于一直以来建模的难点——封头部分，用传统建模软件分段划分，分段设置不同的是，ACP里Look-up Tables 功能可以基于Excel 表格或Python生成的数据进行变化， 解决封头上纤维缠绕角度和复合层厚度难以准确定义的问题。 定义方向为沿气瓶轴向， 封头的基面为坐标零点，则螺旋缠绕的单元角度和厚度的具体变化如图3所示。

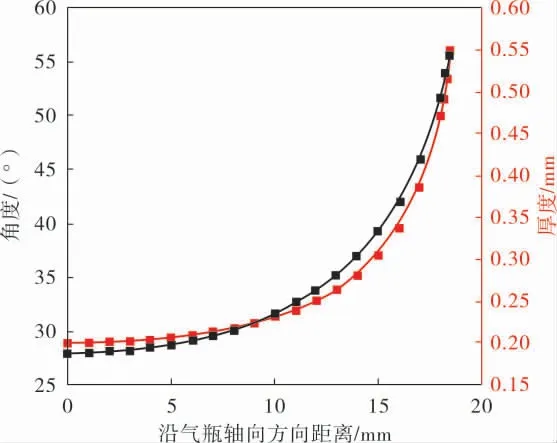
图3 封头处螺旋缠绕的单元角度和厚度沿气瓶轴向的变化

1.4 边界条件与载荷

根据气瓶受压的实际工况，选定边界条件由两部分组成：一是内载荷；二是自由度约束条件。且要考虑瓶口处的作用在端塞上的内压，其载荷可通过在瓶口上施加等效轴向拉应力代替；然后瓶口施加轴向约束和旋转约束，即：

式中 D1、D2——气瓶口的内、外径；

p——内压；

T——轴向拉应力；

下标i——不同的载荷步。

筒体由截面厚度不断增加的过渡段和等厚段组成，为了探究基体的开裂过程，将渐进失效压力设置为一个工况，采用不断增加内压的方式（每个内压增量Δp=1MPa）进行加载，直到气瓶计算不再收敛为止。 具体操作为：内压从零均匀向设定值62MPa变化， 同时瓶口拉应力也随着内压的不同而相应发生变化， 内压每个子步增加1MPa，瓶口拉应力增加0.43MPa，直到气瓶发生爆破为止。

2 结果与分析

2.1 渐进失效分析与退化准则

针对刚度退化参数这一问题，在许多单层板的失效准则（如Tsai-Hill、Hoffman、Tsai-Wu）被提出后，Chang F和Chang K提出Chang-Chang失效准则，之后被广泛引用［8］。 Tan S C分析了层合板渐进损伤， 在Chang-Chang失效准则的基础上，提出不同的损伤形式需要用不同的参数，但没有给出刚度折减系数［9］。 Camanho P P和Matthews F L借鉴了Hashin失效准则， 按照Tan的参数退化方式，提出了相应的折减系数，该方案在求解薄板问题的失效上，与实际值吻合较好［10］，笔者采用这一方案，其参数退化方案如下：

基体拉伸 Ey′=0.2Ey，Gxy′=0.2Gxy，Gyz′=0.2Gyz

基体压缩 Ey′=0.4Ey，Gxy′=0.4Gxy，Gyz′=0.4Gyz

基体纤维剪切 Gxy′=0，Pr′=0

分层 Ex′，Prxz′=0；Gxy′，Gyz′=0

纤维拉伸 Ex′=0.07Ex

纤维压缩 Ex′=0.14Ex

2.2 基体开裂损伤

由前所述，基体强度相比纤维低很多，故失效也发生在纤维还没有失效之前， 根据二维Hashin失效准则，基体因拉伸开裂的损伤系数为：

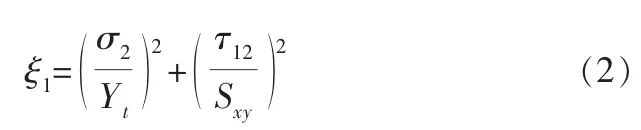
ξ1＞1视为失效，退化方案为：Ey′=0.2Ey，Gxy′=0.2Gxy。

在ACP-Post中，工作压力下，可以看出基体开裂的损伤系数各处并不相同，环向层损伤系数普遍接近0。 以图4为例，筒身处基体开裂损伤系数较大，且在筒中段处系数普遍平稳、较大，靠近过渡段则逐渐减小，且保持平稳，进入封头段后迅速下降为接近0，总体来说，损伤系数变化连续、平稳，中段等厚段大于两端，螺旋缠绕层损伤系数大于环向缠绕层。因此，可以预见在内压载荷不断增加的情况下， 基体开裂系数将在筒身段最先出现，而后再出现在封头上。 为了更加清楚，接下来将分别分析不同的损伤系数变化规律。

图4 缠绕层基体损伤系数

2.2.1 筒体上基体开裂

如图5所示为筒体上基体随内压增大的开裂过程，为了更清楚地展示这个过程，图6列出了不同纤维层开裂过程中的损伤系数，鉴于损伤系数变化近似呈现对称关系，本节对称地选取筒体含瓶口部分的一段。

图5 筒体基体开裂过程的损伤系数

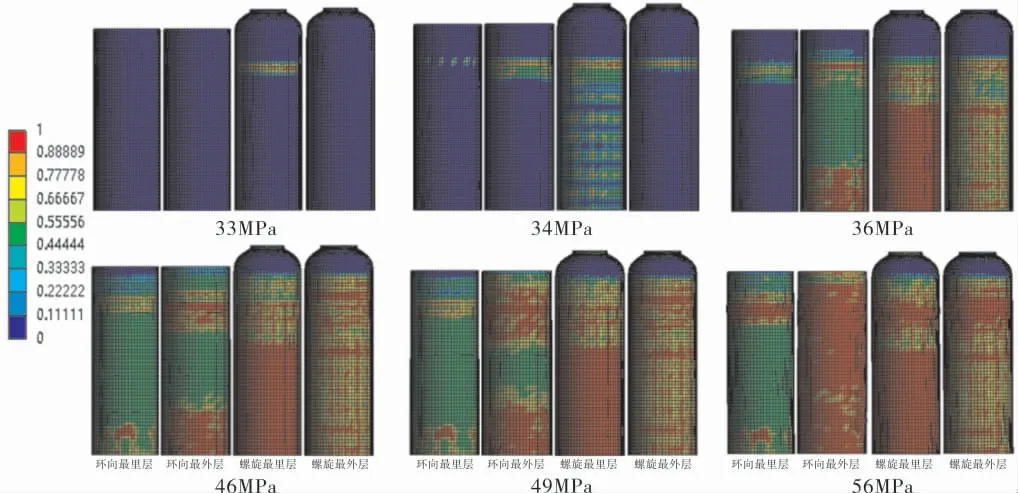
图6 不同纤维层基体开裂过程的损伤系数

从图5中可以看出，内压为33MPa时，等厚段筒体部分的第3层纤维层，即28°螺旋纤维最里层开始出现基体损伤，损伤系数最大值超过1，即认为该处出现了基体失效，其他的筒体环向和螺旋缠绕层还保持完好， 但其应力值却已达到很高；内压为34MPa时，两个螺旋缠绕层都出现了失效，同时， 环向缠绕层最外层也出现失效； 内压为36MPa时，失效的范围进一步快速延伸，螺旋缠绕层最里层的等厚段几乎全部失效，环向缠绕层最外层的失效范围显著扩大，筒体等厚段靠近对称面部分失效，而环向缠绕层最里层也出现了损伤系数超过1的失效单元；内压达到46MPa时，螺旋缠绕层基体损伤系数由等厚段扩展到过渡段，环向缠绕层最里层失效范围快速增加，最外层也出现了过渡段的损伤；内压为49MPa时，环向缠绕层最外层失效范围进一步扩大，只有与封头连接处和等厚段上一部分还未处于失效状态，其他纤维层也出现不同程度扩大；直到内压为56MPa时，螺旋缠绕层和环向缠绕层的大部分单元都已出现了沿纤维正交方向的基体失效，产生刚度退化。

2.2.2 封头上基体开裂

封头的纤维层相对筒体的来说，出现失效单元的情况较晚，在内压达到36MPa时，封头瓶颈段接近了失效极限；内压为38MPa时，瓶颈纤维层曲率过渡处首次出现失效单元， 呈现点状分布，失效后进行刚度退化并不断延展；内压为46MPa时，失效区域由点状发展为环形，向下更大的区域接近了失效极限，同时封头和筒体上的过渡段也出现了明显的损伤系数增长；内压为48MPa时，封头和筒体上的过渡段首次出现损伤系数超过1的情况；内压为56MPa时，损伤面积迅速扩大，瓶颈处的失效区域向下延伸扩展，向筒身过渡的区域也出现了沿环向的扩展，这种情况一直持续到内压为59MPa筒体纤维接近断裂失效（图7）。

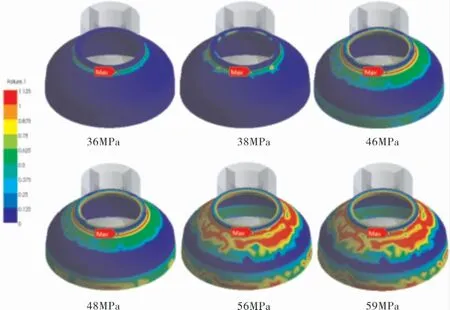
图7 封头上基体开裂过程的损伤系数

2.3 纤维断裂损伤

前已述及，纤维是复合材料气瓶中主要的承压部分， 纤维部分的失效将带来刚度的迅速下降，显著降低气瓶的承载能力，也意味着结构逼近整体失效。根据二维Hashin失效准则，纤维断裂损伤的失效系数表达式为：

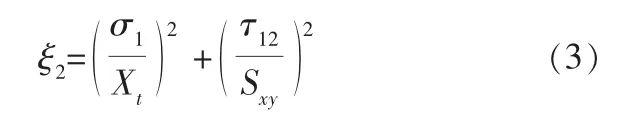
当ξ2＞1时， 视为纤维断裂失效， 其刚度乘以0.07的折减系数。 如图8所示， 内压从51MPa到56MPa时，最大纤维向应力逐渐增大，并从筒体中部移到靠近筒体和封头过渡段处，随着内压的不断增大，60MPa时气瓶发生爆破，位置在筒体中部靠近封头过渡段处，因此近似选取筒体段复合纤维层的一半分析气瓶的失效过程。

图8 气瓶结构失效形貌

图9a、b所示分别为筒体纤维和对应内压下的不同纤维铺层的损伤系数，由左到右分别为环向缠绕层最里层、环向缠绕层最外层、螺旋缠绕层最里层，螺旋缠绕层最外层。 可以看出，内压为56MPa时， 缠绕层环向最外层和螺旋最外层逼近损伤临界值；内压为58MPa时，环向最外层的直筒段靠近封头的过渡区出现若干失效点， 同时，同样位置的螺旋纤维层也出现了环形纤维损伤系数大于1的区域， 而环向最里层接近失效但未出现失效区域， 表明结构仍然有一部分承载能力；内压为60MPa时， 环向最里层的失效面积迅速扩大， 且螺旋缠绕层也出现了显著的失效区域扩展，同时环向最里层也出现了失效区域，形变显著扩大，可以认为结构发生了失效；内压为61MPa时， 由于失效单元完成了纤维方向的刚度退化，导致失效区域快速扩展， 因此认为内压60MPa是结构的极限承载压力。

2.4 内胆破裂损伤

图9 筒体纤维和缠绕层纤维断裂失效

图10为气瓶内胆出现泄漏过程筒体的Von-Mises应力分布云图， 可以从中看出， 内压为56MPa时，筒体大部应力处于内胆材料屈服强度270MPa以上，表明筒体大部处于屈服，最大值出现在封头与筒体的连接处， 最大应力为303.06MPa。 DOT-CFFC标准要求缠绕层随着内压的持续增大，纤维持续刚度退化，内胆应力不断升高而局部塑性断裂，先行泄漏，即“未爆先漏”现象；内压为58MPa时，气瓶出现局部泄漏，内胆的Von-Mises 应力在纤维断裂初始位置达到398.22MPa，超出了极限强度320MPa，放大图中可见内胆在纤维断裂初始位置处环形区域出现了开裂，发生泄漏，而复合材料层还未整体失效，因此，满足标准的未爆先漏要求；随着压力的继续增大（60MPa），裂纹向两端扩展，位移显著增大，内胆爆裂，位置在气瓶侧壁上。

3 实验验证

制得实验用气瓶样瓶两个（样瓶1、2），进行水压爆破试验。 采用J-91-6 爆破试验装置，DSY200试压泵（100MPa量程，1.6级） 进行增压实验，得到水压爆破试验曲线（图11）。 可以看出，样瓶爆破压力分别为56.3MPa和57.0MPa，均高于最小爆破压力44.2MPa，实验值相比理论值60MPa偏小， 可能是由于生产制造过程中的微小缺陷，造成局部应力集中进而降低结构的承载能力，与理论值误差大约为5%左右，故上述理论分析是可接受的。

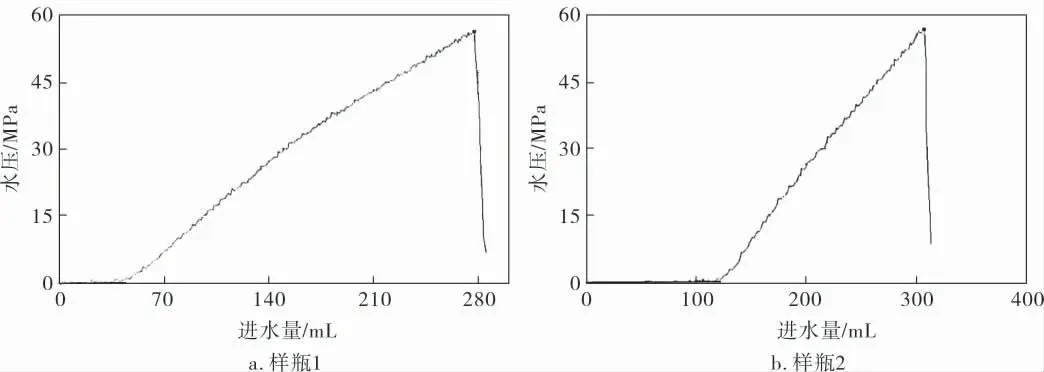
图11 水压爆破试验压力与进水量曲线

观察破口形貌， 气瓶破口位置在气瓶上部，破口长度分别为108、113mm， 破口宽度分别为51、54mm，可以看出由于纤维断裂引发结构刚度急剧下降，进而导致爆破失效。

4 结论

4.1 内压为33MPa时，螺旋缠绕层最里层开始出现基体损伤；内压为34MPa时，两个螺旋缠绕层都出现了失效， 环向缠绕层最外层也出现失效；内压为36MPa时，失效的范围进一步快速延伸，环向缠绕层最里层也出现了损伤系数超过1的失效单元；内压为46MPa时，螺旋缠绕层基体损伤由等厚段扩展到过渡段；内压为49MPa时，只有与封头连接处和等厚段上一部分还未失效； 直到内压为56MPa时， 螺旋缠绕层和环向缠绕层的大部分单元都已出现基体失效，产生刚度退化。 封头纤维层出现失效单元的情况较晚，内压为36MPa时，封头瓶颈段接近失效；内压为38MPa时，曲率过渡处首次出现失效单元；内压为46MPa时，失效区域由点状发展为环形；内压为48MPa时，封头和筒体上的过渡段首次出现损伤系数超过1的情况； 内压为56MPa时，瓶颈处的失效区域向下延伸扩展，向筒身过渡的区域也出现了沿环向的扩展。

4.2 内压为56MPa时，环向缠绕层最外层和螺旋缠绕最外层纤维接近断裂失效；内压为58MPa时，环向缠绕层最外层的直筒段靠近封头的过渡区出现失效点，同时，同样位置的螺旋缠绕层也出现了环形损伤区域；内压为60MPa时，螺旋缠绕层也出现了显著的失效区域扩展， 同时环向缠绕层最里层也出现了失效区域，认为结构发生了失效。

4.3 由于纤维的断裂会显著降低刚度，气瓶内胆在纤维断裂初始位置应力明显增大， 内压为58MPa时，内胆的上述位置Von-Mises应力超出最大应力，出现开裂泄漏，满足未爆先漏要求。

4.4 通过与实验对比，实验值偏小可能是由于生产制造过程中的微小缺陷造成局部应力集中，进而降低结构的承载能力，理论气瓶爆破压力与实际气瓶爆破压力的误差范围大约为5%， 可认为数值模型较好地反映了气瓶的临界压力大小。