数学抽象及其教学实践

陈宝青 雒义霞

[摘  要] 数学抽象是数学学科核心素养的第一个要素，教师站在数学抽象素养培养的机制角度理解并实施其教学，是数学抽象素养落地的前提. 教师要从学生思维角度理解数学抽象，进而认识到数学抽象的本质是数学抽象概括能力培养. 数学抽象过程，对应的就是学生的数学抽象概括过程，因此培养学生的数学抽象概括能力，实际上就是在培养学生的数学抽象能力，也就是在提升学生的数学抽象素养.

[关键词] 高中数学;数学抽象;教学实践

数学抽象是数学学科核心素养的第一个要素，也是数学学科异于其他学科的本质特征之一，作为抽象的下位概念，数学抽象强调在抽象的过程中运用数学的思维去加工抽象的对象，因此从这个角度讲数学抽象是数学最基本的思维方式，它具有纯粹性、精确性、理想化、模式化、形式化等特点. 在传统的数学教学中，数学抽象的地位是比较高的，但是从教学经验以及一些教学文献来看，对数学抽象在教学中的重心，似乎更多地落在抽象过程与结果的经验化表达上，谈及数学抽象的过程，往往也只是用数学抽象这个概念去表达，对于数学抽象背后所运用的数学思想方法，往往着墨不够. 其背后的原因是因为重视不够，还是因为研究深度不够，这是值得思考的. 核心素养重视培养学生的必备品格与关键能力，这不是一个简单的任务，教师站在数学抽象素养培养的机制角度理解并实施其教学，是数学抽象素养落地的前提. 大量研究表明，高中数学教学中的数学抽象，对学生的抽象概括能力有着较大的依赖，在数学教学中应当重视学生抽象概括能力的培养，并且应当以之为支点，去撬起数学抽象的教学.

从学生思维角度理解数学抽象

首先必须强调的是，数学抽象的主体应当是学生，数学抽象是学生运用数学思想方法进行抽象的过程. 对数学抽象的研究，更应当站在学生心理的角度去理解，去实施. 上面已经阐述了从抽象概括能力培养的角度，去实现数学抽象素养的提升.

通常情况下都认为数学抽象概括能力是数学思维能力，也是数学能力的核心. 数学抽象概括能力具体表现为这样的几种能力：发现在普遍现象中存在着差异的能力、在各类现象间建立联系的能力、分离出问题的核心和实质的能力、由特殊到一般的能力、从非本质的细节中使自己摆脱出来的能力、把本质的与非本质的东西区分开来的能力、把具体问题抽象为数学模型的能力等方面. 对于这几种能力的理解，站在学生的角度应当有這样几点理解：一是数学抽象概括能力要引导学生在具体的情境中，发现普遍现象之间的差异，显然这是指数学视角下的差异，需要的也是学生的数学视角，这一点原本就体现着史宁中教授对数学抽象的界定，即用数学的眼光看事物;二是数学抽象概括能力要引导学生完成数学判断，数学判断的过程就是从数量关系、图形关系中抽象出数学概念以及概念之间的关系（数学规律）的过程，这个过程的结果是用数学语言来表达的;三是数学抽象与概括最终表征为数学概念、数学规则、数学命题、数学模型、数学思想、数学方法、数学结构、数学体系等等.

根据教学经验可以发现，高中学生在这些方面具有一定的能力基础，但是能力运用的逻辑并不清楚，更多的是一种学习经验支撑下的能力运用. 这样的能力运用过程理解为默会知识，而要想以抽象概括能力为抓手，培育学生的数学抽象素养，就要将这种隐性的默会知识变成显性的门类培养过程.

数学抽象中数学概括教学实践

将数学抽象作为一种宏观视角，而将数学抽象概括能力的教学作为抓手，这是有效的教学策略. 更加精确的研究表明，数学抽象通常要经历感知与识别、分类与概括、想象与建构、定义与表征、系统化与结构化等五个阶段，而为了更好地发展学生数学抽象素养，数学教学应夯实抽象的基础，指导抽象的方法，重视抽象的过程，加强学生抽象实践，加强对抽象素养的评价. 将这样的表述与数学抽象概括能力培养结合起来，有同行建议在教学过程中，利用弱抽象概括教学引出新知，利用强抽象概括教学巩固新知. 所谓弱抽象与强抽象，若抽象强调在原型中选取某一个特征或者某一个方面进行抽象，其前提是这个原型的特征比较丰富，也正是因为如此，人们在数学抽象的第一步往往选择的都是弱抽象;相应的，如果原型的特征比较贫乏，弱抽象无法发挥作用，就必须运用强抽象. 例如，在函数概念的建构中，教师往往都会给学生提供函数关系比较密切的实例，如一个做斜抛运动的物体，其距水平地面的距离（高度）与运动时间之间的关系. 对于高中学生而言，这样一个关系早在物理学科的学习中就已经遇到过，因此学生可以很快地建立起h=v0t-■. 在这里，斜抛运动是一个比较形象具体的生活实例，而函数关系式h=v0t-■则是一个抽象的数学表达式，因此学生的抽象过程实际上就是一个弱抽象过程，因此在实际教学中几乎看不到学生，有一个明显的抽象过程，学生学习过程中一下子发生的就是概括. 因此教师在教学中，只要将这个隐性的过程变成显性的过程，就可以比较直接地实现抽象概括能力的培养.

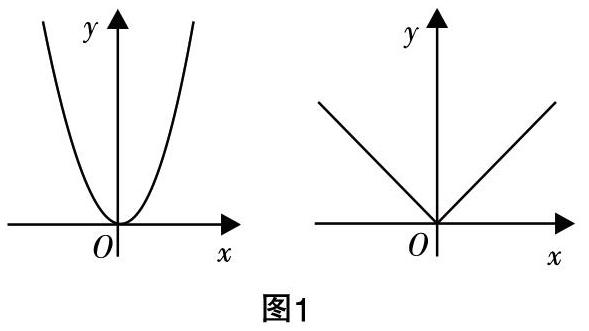
再看另外一个例子：在函数的奇偶性教学中，由于学生生活中缺乏对函数奇偶性提供支撑的实例，因此教师只可能从抽象的数学素材中寻找例子，来给学生创设情境. 如图，分别是两个函数图像，让学生去分析、比较，看两个函数有什么共同的特征？

这是一个非常重要的问题，是引导学生在原有知识基础上进行抽象概括的驱动力. 学生在抽象的过程中，只能通过函数图像的形状，发现其“对称性”;但是这个时候的对称性只是一种表象认识，而不是数学认识，因此必然要经历一个概括的过程，这个概括是对两个图像分析综合结果的概括——概括当然是指向对图像上坐标的分析的，两个图像上x与-x对应着同一个y值，这在数学上意味着什么？显然，从函数的角度来看，就是f（x）=f（-x）. 这个时候的抽象概括过程并没有结束，教师还需要引导学生思考，除了f（x）=f（-x），是否还存在其他的情形？

在这样的学习思路中，用抽象概括驱动起学生的思维，学生可以比较顺利地建构起关于函数奇偶性的认识. 而这样的一个抽象过程，由于提供给学生的抽象素材中，关于函数奇偶性的特征并不明显，因此学生的抽象就是强抽象.

从抽象概括能力培养的角度来看，从学生思维的角度来看，在上述两个案例的教学过程中，学生经历了数学抽象的过程，经历了运用数学语言概括数学抽象结果的过程，这两个过程都是指向思维的，无论是基于函数解析式的思维，还是基于函数图像的思维，都为数学概括奠定了基础，而将数学抽象与数学概括结合起来，数学抽象概括的过程都成为数学抽象素养形成的有力支撑.

基于抽象概括视角的数学教学

数学的研究对象，也就是数与形，都是数学抽象的产物，高中生在数学学习的过程中，在用自己的思维加工大脑当中相对熟悉的数形经验时，又或者是加工形象的事物，然后通过抽象获得的数形的时候，都是离不开思维的. 相应的数学抽象过程，对应的就是学生的数学抽象概括过程，因此培养学生的数学抽象概括能力，实际上就是在培养学生的数学抽象能力，也就是在提升学生的数学抽象素养.

研究数学抽象概括的基本界定可知，抽象概括能力是面向具体的、生动的实例的，在抽象概括的过程中，教师引导学生发现研究对象的本质，并从给定的大量信息材料中概括出一些结论，就能将其应用于解决问题或做出新的判断. 相对于传统的教学而言，这是一个新的教学视角，某种程度上讲也对应着教师的教育哲学. 数学教师的教育哲学影响着自己对教学方式的选择，影响着对学生学习过程的判断，对于数学教师而言，对数学抽象概括的认识可以成为数学教育哲学的基本组成部分，影响着教师在数学抽象教学中的选择.

笔者认为数学抽象是数学学习的基础，而数学抽象概括作为数学抽象的实质，又是基础的基础，认识到这个基础性作用，也就决定了在实际教学中必须高度重视数学抽象的教学. 笔者的教学实践表明，在教学设计中带着数学抽象概括的意识，在教学实践中带着数学抽象概括的培养技巧，在教学反思与教学评价的过程中，让学生认识到数学抽象和数学概括的价值，就可以让数学抽象在教学中真正得以落实，从而也就为数学学科核心素养的落地提供有力的保障.

总的来说，数学抽象是高中数学教学研究的一个热门话题，抓住数学抽象的本质进行教学研究，是从表面走向本质、从经验走向智慧的重要思路，每一个高中数学教师都应当建立起这样的认识，如此可以奠定核心素养培育的基础.