V型拱塔斜拉桥状态评估基准有限元模型研究

王 伟， 张玉平

(1.重庆中科建筑工程质量检测有限公司， 重庆 400080；2.长沙理工大学土木工程学院， 长沙 410114)

引 言

近年来随着人们生活水平的提高，审美要求越来越高，尤其是对城市桥梁的景观诉求越来越强烈。双拱塔斜拉桥因其受力合理、造型柔美轻盈，变化多端等特点建造得越来越多。双拱塔构成的V型不仅寓意胜利也有开放包容之意，同时兼具拱桥与斜拉桥的美学特点，受到设计师们的青睐[1-2]，如沈阳三好桥、荔波官塘大桥等。一般桥梁初始有限元模型是根据施工竣工图纸建立的，这样建立的模型是“完好”的，但是桥梁在长期运营过程中会形成一些新的病害以及遭受火灾、船撞等意外情况使得实际结构存在损伤，这就造成了理论模型与实际结构之间的误差。为了使初始有限元模型能够准确、真实地反映桥梁结构在当前状态下的实际受力情况，从而得到桥梁状态评估的基准有限元模型，就需要对初始模型进行修正[3-4]。

李志刚[5]、张国刚[6]等学者基于环境激励所获得的动力特性参数对桥梁有限元模型进行了修正，但是环境激励下的数据采集噪声较大，并且不同动力参数识别方法所获得的动力特性也有差别，此外修正后的动力模型又不能够准确地反映出结构的静力特性。姚南[7]、李旺东[8]等学者基于静力实测数据对桥梁进行了有限元模型修正，静力实测数据虽然较环境激励下获得的动力参数更为精确但是实测数据量较少。基于此，本文采用联合结构静力荷载试验中量测较为精确的挠度值与动力荷载试验中获得的实测自振频率来对初始有限元模型进行修正，这样既克服了单纯运用动力参数的片面，又避免了静力挠度实测数据量较少的局限。具体为：首先对V型拱塔斜拉桥开展了静动力荷载试验，得出结构当前状态下的受力情况及响应，然后运用模型修正技术，利用实测与理论差值的最小二乘原理，结合实测挠度与频率数据对初始有限元模型进行修正与验证，最后利用静动力荷载试验中获得的其他实测参数，如其他工况中的实测挠度与模态振型等来校验修正后模型的准确性，并以此作为桥梁状态评估的基准有限元模型。

1 工程概况及模型建立

1.1工程概况

大桥为跨径组合2×90 m V型钢拱塔斜拉桥，主梁采用C55混凝土，单箱四室预应力混凝土箱梁，箱梁全宽34 m，梁高2.8 m，顶底板厚0.28 m，在桥塔处增加到0.55 m；腹板厚0.45 m，在桥塔处增加到0.75 m。桥塔造型为双钢拱塔V字型，钢拱塔中心倾斜20°，采用Q345C级钢材，单箱单室断面。斜拉索和水平拉索采用标准强度为1670 MPa的高强镀锌平行钢丝拉索，全桥共60根。设计荷载为城—A级(双向6车道)。

1.2模型建立

采用MIDAS CIVIL 2010有限元软件建立空间有限元模型，由于该桥主梁截面为闭口截面，故采用“鱼骨梁模型”来模拟主梁，如图1所示。其中，主梁、主塔(墩)及承台采用空间梁单元模拟，斜拉索和水平拉索采用桁架单元模拟，并考虑拉索索力对结构几何刚度的影响；桥梁支座按照实际约束情况采用弹簧单元模拟，弹簧单元刚度根据支座厂家提供数据进行计算。

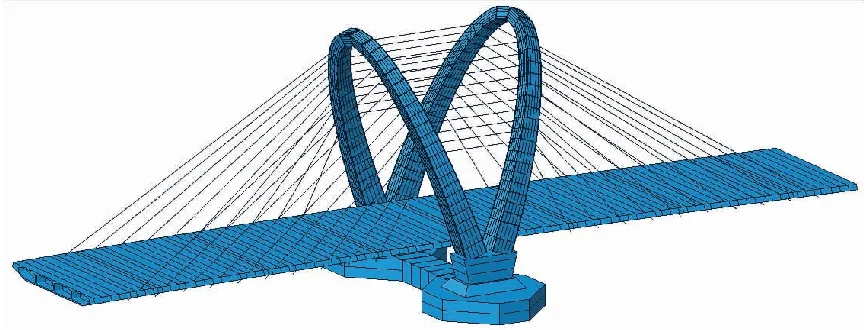
图1 空间有限元模型

2 荷载试验及评价

2.1荷载试验方案

结合《试验规程》要求与桥梁特点[9-10]，此次静载试验选取5个控制截面，即主跨主梁最大正弯矩(k1)、主塔附近主梁最大负弯矩(k2)、索塔最大负弯矩、塔顶最大纵飘、索力增量最大的拉索等截面。

采用三轴加载车等效模拟设计活载效应，根据荷载效率系数η来确定静力试验的现场加载荷载[9]。鉴于钢拱塔为工厂预制现场拼装，受施工环境与工艺影响较小，有限元模型的索力值亦是按照实测索力输入，可不进行修正。混凝土主梁的施工过程与材质特性影响因素较多，故此处主要介绍k1与k2加载工况(图2)，用于后续的模型修正。其中，当k1截面采用2排横向6辆(2×6=12辆)时，k2截面采用3排横向6辆(3×6=18辆)载重300 kN的加载车布置时，η分别为1.01与0.88，满足《试验规程》中该值在0.85～1.05范围内的要求[10]。

图2 桥梁荷载试验主要控制截面及测点布置(单位：cm)

2.2试验结果与评价

k1与k2控制截面加载工况下主梁主要挠度测点实测值见表1。其中挠度值为负表示结构下挠，正值表示上挠。

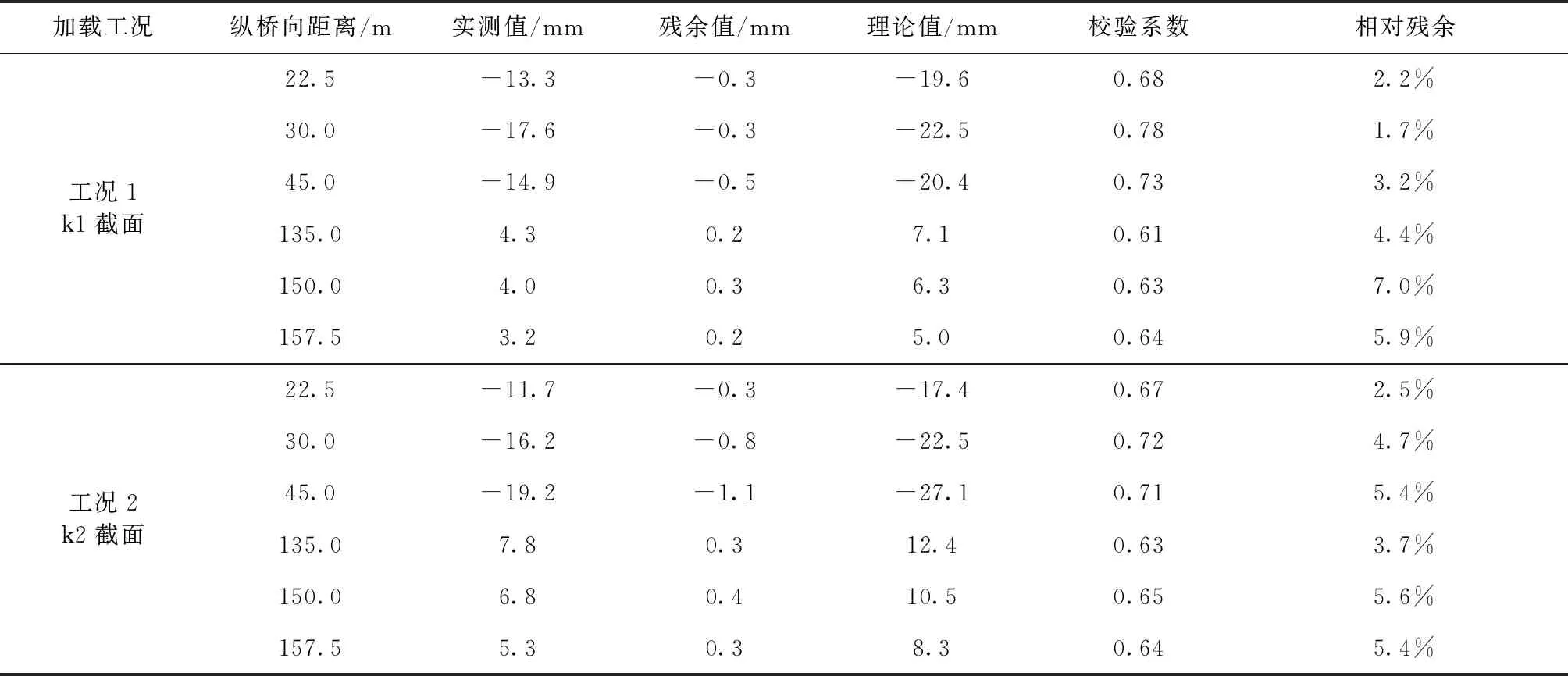
表1主梁主要挠度测点对比分析

由表1可见，主要挠度测点校验系数在0.61～0.78之间，说明实测主梁结构刚度大于理论值，具有一定的安全储备，表明结构整体刚度符合规范要求，另一方面也说明实际结构的刚度要大于初始有限元模型所得刚度；主要挠度测点相对残余在1.7%～7.0%之间，远小于20%，满足《试验规程》的要求[10]，表明结构处于弹性工作状态，整体性能良好。

利用环境激励下桥梁的加速度时程信号，跑车试验和跳车试验后的余振信号来获取桥梁结构的实际自振频率与模态振型以及阻尼比。各动载试验工况下桥梁竖向前四阶的频率与阻尼比见表2。

表2竖向前四阶的自振频率与阻尼比

从表2中可发现，3种方法得到的实测自振频率较为接近，且均高于理论值，表明结构的实际刚度要优于初始有限元模型刚度，这与初始有限元模型未考虑实际结构的横隔板、局部加劲肋有关；结构竖向前四阶实测阻尼比在0.023～0.028之间，属于小阻尼振动，处于正常范围。

3 模型修正及校验

3.1初始模型修正

为了使初始有限元模型能够准确地反映结构当前受力状况，为桥梁状态评估建立基准有限元模型，需要对初始有限元模型进行修正[11]。实质上，模型修正就是不断调整模型关键参数来使得理论值与实测值之间的差值最小，从而让有限元模型能够真实反映出实际结构当前状态下的受力状况[12-13]。影响有限元分析结果的结构参数有很多，修正参数的选择一般采用灵敏度分析[14]，有限元分析中，灵敏度可表达为一阶偏导函数的形式：

(1)

基于上述思想，利用静力荷载试验中k1控制截面加载工况下的实测挠度与动力荷载试验中结构的竖向前四阶自振频率来修正初始有限元模型[15-17]。联合静动力荷载试验的目标函数：

(2)

式中：g(x)为目标函数；dex、fex分别为荷载试验实测挠度与频率值；dca、fca分别为理论计算挠度与频率值；λi、λj分别为位移和频率在g(x)中的权重；n、m分别为用于修正的挠度测点与自振频率的数目。

3.2修正后模型验证

模型修正前、后k1截面加载工况下各测点的挠度曲线对比如图3所示。

从表1与图3中可发现，模型修正前，即初始有限元模型的理论值与实测值的误差最大达到39%，表明初始模型并不能够真实准确地反映出桥梁当前的受力状况。模型修正后，挠度误差均在10%以内，最大为8%，与实测值吻合较好，且挠度曲线变化趋势一致，表明修正后的有限元模型能够更好地反映出实际桥梁结构的静力性能。

图3 模型修正前、后k1截面挠度曲线对比

模型修正后，结构竖向前四阶实测与理论自振频率对比见表3。

表3模型修正前、后竖向前四阶自振频率对比

由表3中可见，模型修正前初始理论自振频率比实测值差距很大，最大误差达到33.7%，而经过修正后的有限元模型分析出来的频率值与实测值基本一致，误差均在6%以内，表明修正后的有限元模型刚度与实际结构一致。

模型修正前、后待修正参数值见表4。

表4模型修正前、后待修正参数值

由表4可见，修正后混凝土的弹模有所提高，这是因为初始有限元模型中材料的物理参数是按照设计规范取值，一般会较实际施工现场的混凝土弹模小，这也与现场检测结果一致，同时初始有限元模型未考虑铺装层对实际结构刚度的贡献；混凝土质量密度也变大，这是由于初始有限元模型未考虑主梁混凝土中普通钢筋的影响，同时也受现场混凝土骨料及配合比的影响。

3.3修正后模型校验

一个良好的数值基准有限元模型不仅要能够准确反映结构的静力荷载响应，还要能够与动力特性吻合，不仅要与修正域内的数据一致或接近，还要与修正域外的数据吻合[14-15]。利用静力荷载试验中获得的其他工况(k2控制截面)中的实测挠度以及动力荷载试验中获得的实测模态振型对修正后有限元模型的准确性进行了校验，模型修正前、后工况二(k2控制截面)挠度曲线对比，如图4所示。

图4 模型修正前、后k2截面挠度曲线对比

从图4中可发现，模型修正前，即初始有限元模型的理论值与实测值的误差较大，有限元模型修正后与实测值吻合较好，误差明显减小，且挠度曲线变化趋势相同，表明修正后的有限元模型计算的理论值能够较好地与修正域外的实测数据吻合，表明了修正后有限元模型的准确性。

模型修正后，结构竖向前四阶实测与理论模态振型对比如图5所示。由图5可见，修正后模型计算的竖向弯曲振型与实测结果吻合良好，模态振型趋于一致，表明修正后的有限元模型能够较好地反映桥梁结构的动力特性。

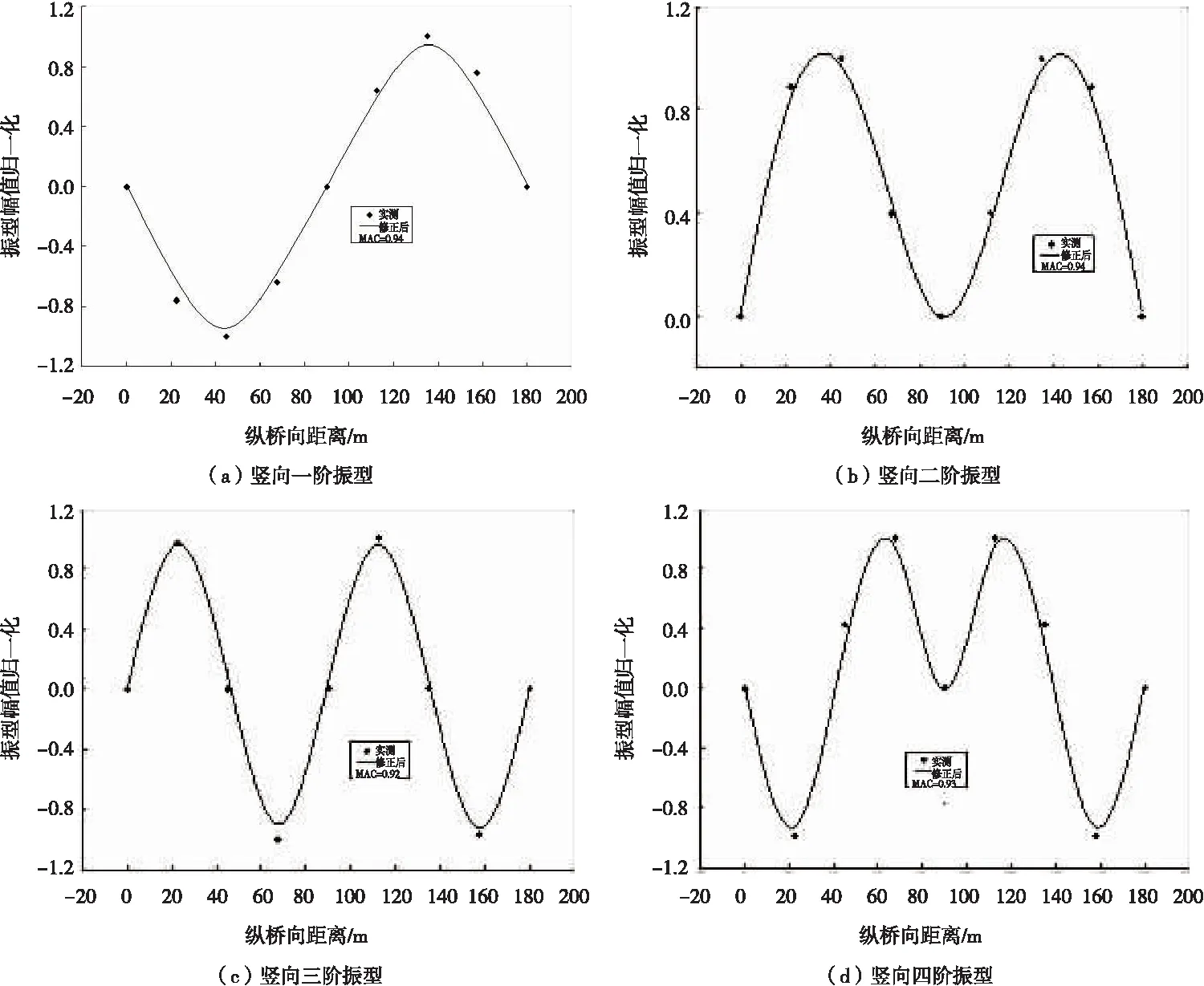
图5 模型修正后结构理论与实测模态振型对比

模型修正前、后动力荷载试验中环境激励下结构动力特性中的模态振型实测与理论之间的相关性[18](MAC值)如图6所示。

从图6中可看出，模型修正前，除第一模态振型相关性(MAC=0.87)较好外，其余三阶相关性一般(MAC≤0.8)，模型修正后，结构竖向前四阶的模态振型相关性系数(MAC)均在0.9以上，模态振型相关性显著提高，表明了模型修正方法的可行性与可靠性。

综上，可认为此时的有限元模型能够表示实际结构，能够以此为数值基准有限元模型进行桥梁状态的评估。

4 结 论

首先对大桥进行了静动力荷载试验，然后运用模型修正技术，对初始有限元模型进行了修正、验证以及校验，得出以下主要结论：

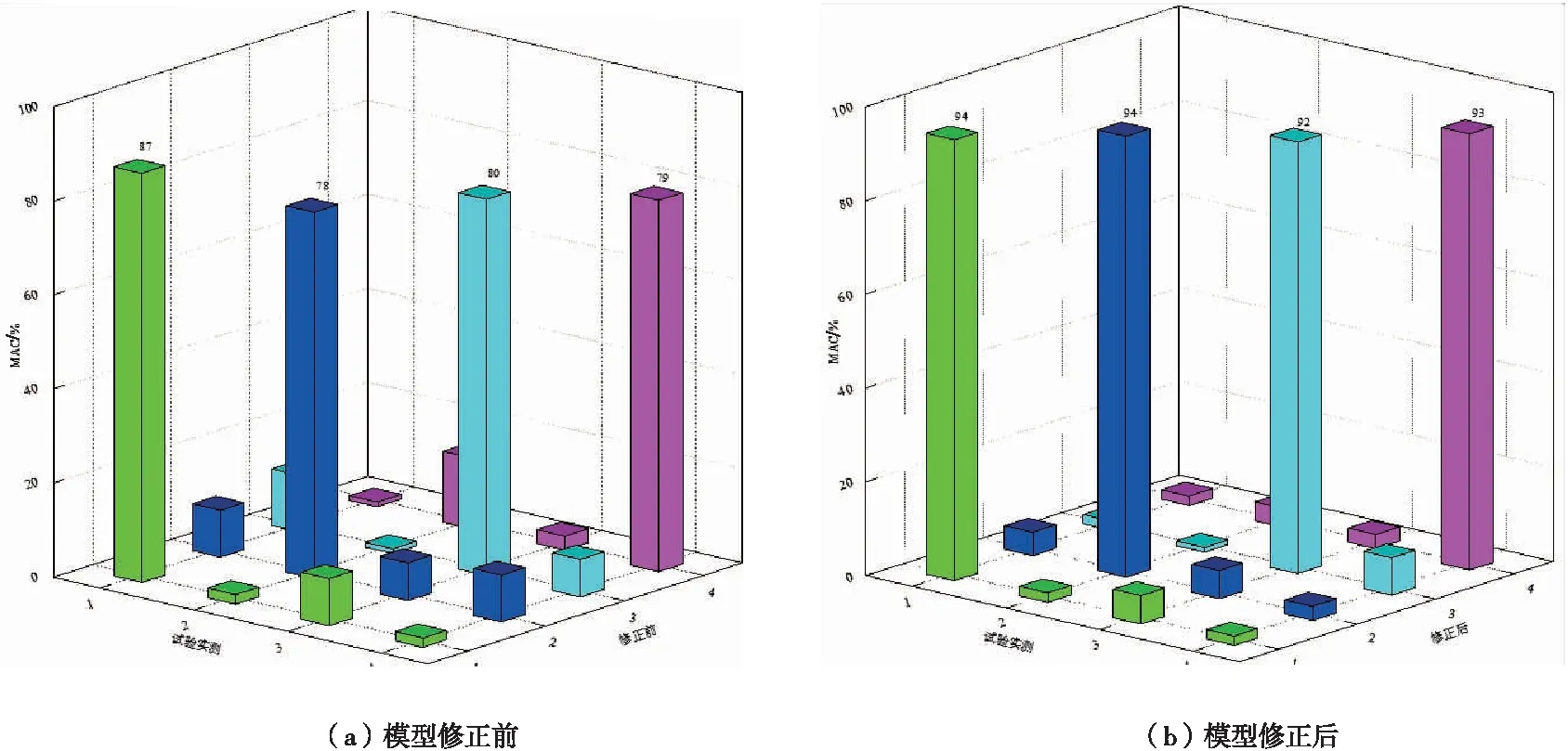
图6 模型修正前、后MAC值

(1)试验荷载作用下各工况主梁主要挠度测点校验系数在0.61～0.78之间，说明主梁实际刚度要大于理论值，具有一定的安全储备，表明结构整体刚度符合规范要求，主要挠度测点相对残余在1.7%～7.0%之间，满足规范要求，表明结构处于弹性工作状态，整体性能良好。不同方法获取的实测自振频率较为接近，且均高于初始理论值，表明结构的实际刚度要优于初始有限元模型。

(2)运用模型修正技术，联合运用实测挠度与频率对初始有限元模型进行了模型修正与验证，修正后的有限元模型各测点挠度理论值与实测值吻合较好，整体变化规律相同，频率也更为接近，表明运用上述方法对初始有限元模型进行修正是正确可行的。

(3)利用荷载试验中获得的其他工况中的实测挠度与模态振型对修正后有限元模型的准确性进行了校验，理论计算挠度与实测值非常接近，模态振型也更趋一致，表明修正后的有限元模型能够真实准确地反映桥梁结构当前状况下的实际受力状态，可以作为桥梁状态评估的基准有限元模型。