永磁同步电动机混沌系统的控制
2020-11-05周群利
周群利
(芜湖职业技术学院电气工程学院, 安徽 芜湖 241006)
引 言
永磁同步电机得益于其高功率密度、高转矩密度、高效率、高可靠性等特性[1-2],在电动汽车、数控机床、航空航天以及舰船综合电力系统等诸多工业及军事领域都得到了广泛应用[3-6]。当永磁同步电动机系统在某些特定参数条件下工作时,会出现混沌现象,具体表现为调速系统的超低频振荡或随机振荡,不规则的电磁噪声[7-8]和控制性能的不稳定等,这些现象直接影响到电机的效率和运行质量,因此,如何消除或利用这种不规则现象成为永磁同步电机传动系统运行中亟待解决的实际问题。国内外学者在不断的研究与探索中,提出了多种控制策略和方法。文献[9]采用延迟反馈控制来抑制电机混沌现象,该方法只需要一个延时处理,算法简单且易于实现,但难以确定延时时间与控制目标的关系;文献[10]采用无源化控制来抑制混沌现象,该方法不用改变系统固有参数,即可实现镇定;文献[11]采用基于扩张状态观测器的自适应滑模策略,解决了部分状态不可测的永磁同步电动机混沌系统控制问题,保证了系统状态能够快速稳定收敛至零点;文献[12]采用非奇异快速终端滑模控制来抑制永磁同步电动机在运行中出现的混沌现象,调速系统中速度环开始用传统PI调节器,电机正常运行。在某些系统参数和工作条件下电机产生混沌现象,此时通过非奇异快速终端滑模控制器取代传统PI调节器进行控制。另外还有自适应控制[13-14]、滑模结构控制[15]、滑模观测器控制[16-18]等方法。受以上文献启发,采用基于微分几何理论的精确反馈线性化方法对永磁同步电动机系统中出现的混沌现象进行控制,仿真结果证明该方法有效,能使系统状态快速稳定地收敛于零。
1 永磁同步电动机混沌系统的数学模型及状态响应
在永磁同步电动机混沌系统的诸多研究成果中,存在一个适合分析永磁同步电动机混沌运动的数学模型[19],其无量纲模型为:
(1)

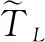

(2)

图时系统的相图
图时系统的相图
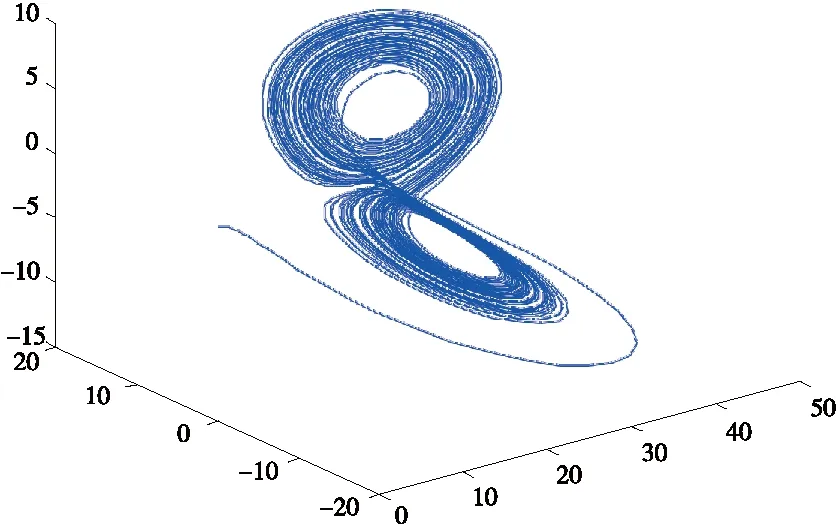
图时系统的相图
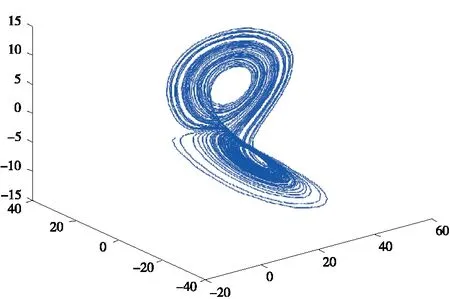
图时系统的相图
2 基于精确线性化方法控制永磁同步电动机混沌系统
针对永磁同步电动机系统在一定参数取值时出现的混沌现象,采用基于微分几何理论的精确反馈线性化方法进行控制,对永磁同步电动机混沌模型(2)施加控制输入u可得:
(3)
受控系统的矢量场f和g分别为:

然后检验系统的能控性和对合条件:
设:
则:
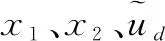
下面检验对合性:
因为零向量是属于任何向量场的集合,故[gadfg]构成一个对合集。
当n=3时,λ(x)应该满足条件:
(4)
(5)
(6)
由式(4)可得:
(7)
由式(5)可得:
(8)
将式(7)代入式(8)得:
(9)
由式(6)可得:
(10)
将式(7)与式(9)代入式(10)并化简可得:
所以,可取λ(x)=x2。

求线性化状态方程及控制律u:
经化简可得
而
(11)
其中:v为新的控制输入。
所以,线性化后系统的方程为:
(12)
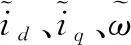
3 系统仿真结果


图5 状态x1施加控制前后曲线

图6 状态x2施加控制前后曲线

图7 状态x3施加控制前后曲线
从图5~图7可以看出,在0 s~200 s内,系统状态变量直轴电流、交轴电流及转速经历了初始的杂乱无规则运动,系统处于混沌状态;在200 s时,对系统施加控制器,系统状态变量直轴电流、交轴电流及转速快速稳定地收敛于系统的唯一稳定的平衡点,原有的混沌状态得到有效控制,显示出所设计的控制器的可靠性。在仿真过程中发现,对线性化后的系统选择不同的极点进行配置时,仅影响系统趋近于平衡点的速度,利用本文方法也可以实现直轴电流、交轴电流及转速对设定目标值的稳定跟踪。
4 结束语
本文采用基于微分几何理论的精确反馈线性化方法对永磁同步电动机混沌系统在其参数均不为零的情况进行控制。通过对微分几何相关定理、引理的运用,对受控的非线性模型进行非线性状态反馈和恰当的坐标变换,变换过程中没有忽略任何高阶非线性项,使非线性系统的控制问题转化为线性系统的控制问题。对线性化后的系统进行极点配置,设计所需的控制输入,仿真结果与理论分析具有一致性,系统状态能够快速稳定地收敛于原点,能有效实现系统的全局稳定。本文的研究为其他非线性不稳定系统的控制提供了一种行之有效的解决思路。
