无人机捷联惯组隔振系统动力学分析与优化设计

段宇星，李 笑，杨 海，杨 强，苏 渤，王 鑫

(1.中国飞机强度研究所，西安 710065；2.北京中航智科技有限公司，北京 100176)

捷联惯组系统是飞机、导弹、火箭等航空航天器的关键设备，主要用途是用于定位、定向、导航以及载体的姿态测量等[1]。其性能以及可靠性直接影响到载体的飞行安全以及正常工作状态。严酷的振动环境可能会远远超过捷联惯组系统自身所能够承受的振动量级，使系统性能与测量精度下降，甚至有可能导致加速度计以及陀螺组件产生零偏，加速度计内部的石英摆片以及陀螺光纤环发生共振乃至组件损坏。振动环境已然成为捷联惯组系统精度和系统稳定性的关键因素。

Yu Tao[2]等人设计了磁流变弹性体对惯组进行了振动控制，提出了一种基于相位控制器来实现振动隔离的实施控制方法。范达[3]等人建立了基于静电悬浮的双级无拖曳天基超静平台的系统模型，提出了一种零刚度隔振减振控制方法。Junchao Chen 等人[4]设计了一种基于运动解耦的振动隔离系统（VIS），建立了六自由度的动力学模型，优化每个自由度的固有频率和衰减系数，使用有限元仿真结果证明了方法的有效性。杨盛林等人[5]针对惯导系统在恶劣力学环境的使用要求提出一种实用的基于橡胶等效动态模量的设计方法。Tuo Zhouhui[6]等人研究了一种IMU 隔振系统的设计方法，针对研究的布局设计了IMU 结构框架与各向同性的隔振器，并使用有限元仿真方法对设计进行了验证。Yongqiang Tu[7]等人研究了橡胶隔振器变形产生的偏角对陀螺组件（RLG）精度的影响，提出了隔振器的3-D Voigt 模型并基于此模型建立IMU 隔振系统的六自由度动力学模型，根据动力学模型导出其动力学方程并计算其数值解，最后通过转盘试验验证了模型的有效性。Donghong Ning[8],D.Capriglione[9],Tian Tan[10],Song Lailiang[11],Zang Chen[12]等人针对IMU 的不同振动环境也分别提出了一些隔振系统解决方法。

本文在Yongqiang Tu 博士研究的基础上，针对某型无人机非解耦安装环境进行分析，建立基于3-D Voigt 模型的六自由度动力学模型及其动力学方程，对模型的动力学耦合状态进行研究。根据模型计算获得适合本文讨论的无人机IMU 隔振系统的性能参数，设计并制造适合工程环境应用的隔振器，为提升无人机捷联惯组的精度与工作性能奠定基础。

1 惯组隔振系统的布局

图1 隔振系统动力学模型Fig.1 Dynamic model of the damping system

捷联惯组的隔振系统属于六自由度系统，由于捷联系统的结构刚度远大于隔振器的刚度，可以将捷联惯组近似为刚体处理。捷联惯组安装示意如图1中所示，其中O点为IMU 几何中心，矢量Ω端点为台体质心。在捷联惯组几何中心位置建立坐标系Oxyz，用U[x，y，z]，Θ[α，β，γ]分别表示捷联系统沿着三个轴向的线位移与角位移。用G[g，0，0]表示重力加速度矢量，其中定义x向为重力方向。

系统的运动方程可以写为:

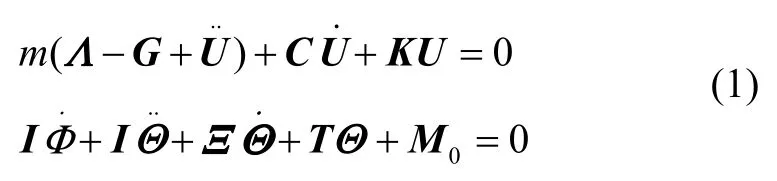
式中:U——IMU 线位移矩阵；m——惯组台体的质量；Λ——输入加速度矢量；Φ——输入角速率矢量；G——重力加速度矢量；C——线阻尼矩阵；K——线刚度矩阵；I——IMU 转动惯量矩阵；Θ——IMU 角位移矩阵；Ξ——扭转阻尼矩阵；T——扭转刚度矩阵；M0——偏心惯性矩矩阵；由几何中心与质心不重合导致。M0=mΩ(Λ-G)，其中Ω为台体质心偏离矢量。

此系统具有6 个自然频率，所有的坐标都相互耦合。即便是沿着轴线上的激励也会使系统在所有方向上产生位移。相互耦合使得振动系统分析难度很高，当模态频率之间相互耦合时，为了降低系统振动，一般的做法是减小系统刚度，将所有的自然频率降低。但这样会导致捷联系统的位移过大，有可能会与外壳发生碰撞。为了减弱或者避免惯组俯仰姿态与角振动对陀螺组件测量精度的影响，必须对隔振系统按照捷联系统的三个敏感轴进行解耦。

在理想情况下包括线振动与角振动的6 个自由度的耦合可以完全解耦为各个独立的单自由度振动，这样我们可以对每个自由度上的振动的研究分别按照单自由度系统进行。

常见的解耦布局形式如图2所示:

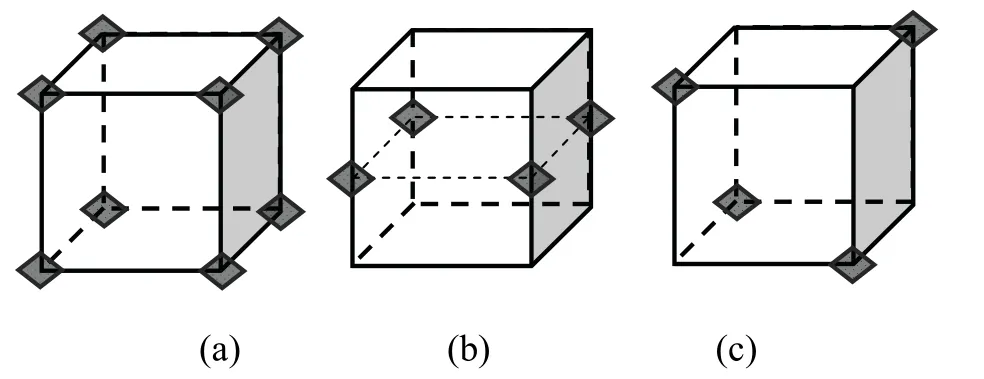
图2 IMU 隔振系统布局方式Fig.2 Layouts of the damping system of IMU

无人机由于结构紧凑，安装空间狭小，一般很难采用图2(a)或者(c)的布局方式。本文讨论的某型无人机所能够提供的接口也仅为平面法兰安装方式，因此IMU 的隔振系统布局方式仅可以选用图2(b)。后述研究分析均建立在图2(b)所示的隔振系统之上。

2 平面布局下IMU 的动态力学行为分析

2.1 完全解耦的模型的建立

对IMU 采用平面对称布局方式，在4 个安装节点上分别安装1 只隔振器，假定所有隔振器的状态完全一致。布局方式以及IMU 状态如图3所示。

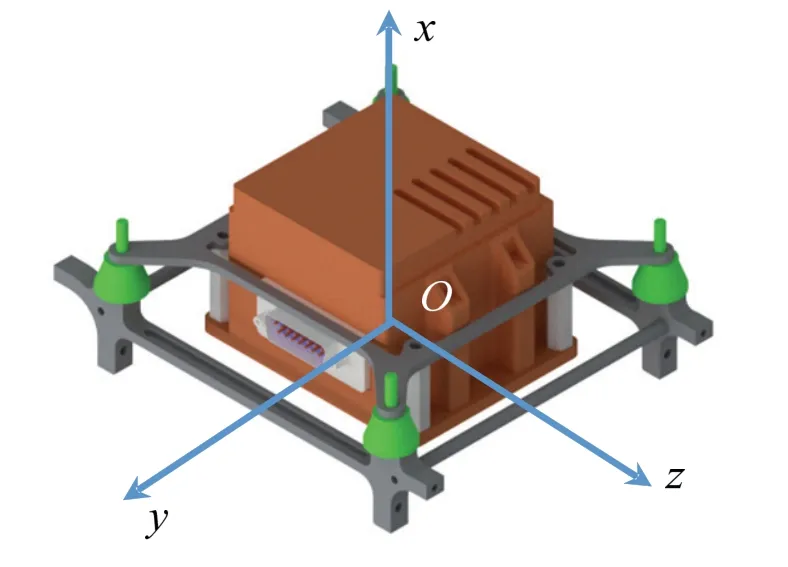
图3 IMU 隔振系统三维模型Fig.3 3-D model of the damping system of IMU

从图3中可以看出，令隔振系统的3 个主惯性轴与坐标轴重合。则有:

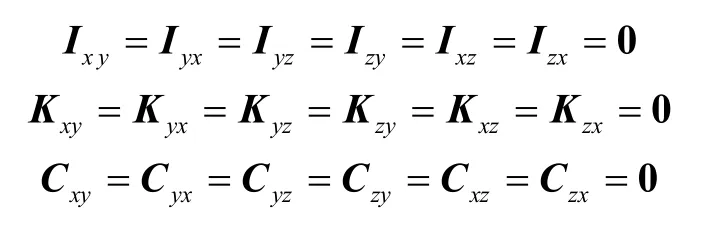
式中I,K,C均为相应方向上的惯性积矩阵,刚度矩阵与阻尼矩阵。再假定质心与刚度中心完全重合，即Ω=0；并考虑系统处于无激励状态，即a=0，则式(1)可以分解为6 个完全独立的方程，亦即对系统进行解耦。则有[13]:

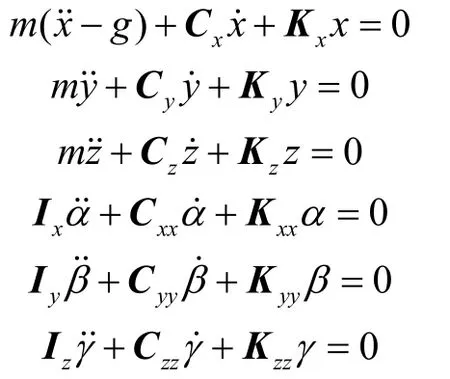
式中:m——惯组台体的质量；C——线阻尼矩阵；K——线刚度矩阵；I——IMU 转动惯量矩阵；x,y,z——三轴向线位移；α,β,γ——三轴向角位移。

2.2 隔振器的状态分析

为了简化模型，可以将隔振器考虑为一个具有一定刚度与阻尼的连接点。所有隔振器所组成的隔振系统的平动刚度与阻尼即为K与C，转动刚度与阻尼即为T与Ξ。

分析每1 个隔振器节点的状态，将隔振器简化分解为沿x，y，z三个轴向的刚度阻尼系统，如图4(a)所示。假定隔振器轴向刚度与阻尼为Ka，Ca，径向刚度与阻尼为Kr，Cr。考虑到隔振器是沿轴向对称而非沿径向对称的结构，而隔振器在隔振系统中的安装方向是轴向与x向平行，则有:

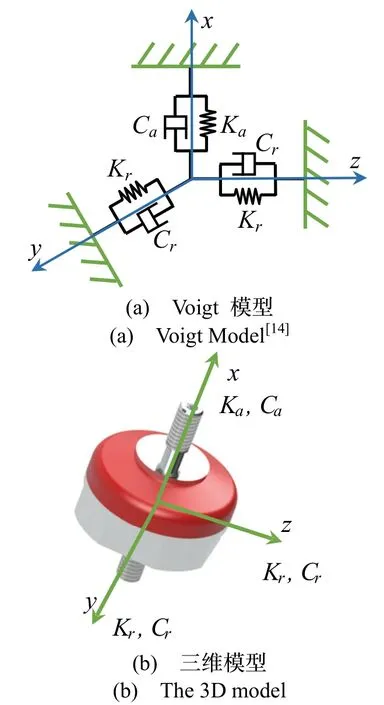
图4 隔振系统隔振器模型Fig.4 Model of isolator of the damping system

整个IMU 隔振系统的动力学状态如图5所示。其中无人机航向与侧向的力学状态如图5(a)所示；无人机垂向的力学状态如图5(b)所示。由于IMU 自身的质心处于台体的几何中心点。分析可知:如果隔振系统在各个方向都完全对称，即可以保证隔振系统的刚度中心与台体质心重合从而解耦整个动力学系统。而在工程实际中隔振系统的航向（y）与侧向（z）一致且完全对称，因此这两个方向的振动状态是完全相同的。但由于隔振器沿轴向（x，无人机垂向）无法在x向刚度中心与几何中心重合。我们考虑Ψ为IMU 几何中心到刚度中心的偏移矢量，从前述分析可知:该矢量沿y,z两个方向的分量均为0，不妨取Ψ=[ψ,0,0]。

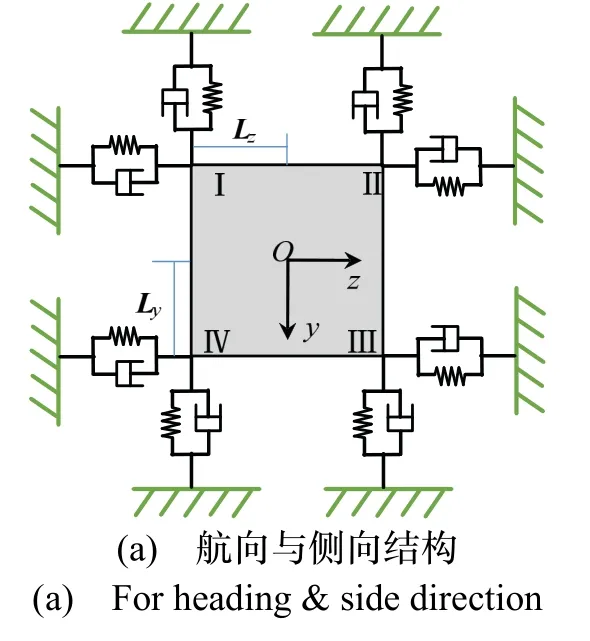
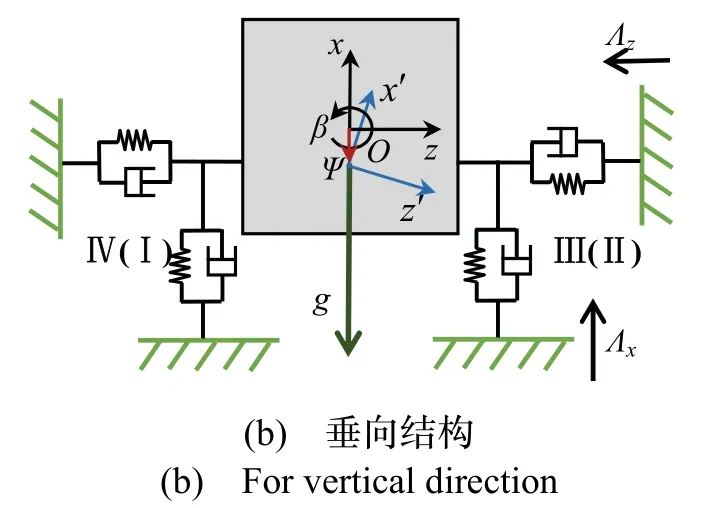
图5 模型动力学耦合状态Fig.5 Dynamical mechanical coupling state of the model

分析图5(b):当IMU 受到垂向的振动激励Λx时，由于偏移矢量Ψ沿y,z两个方向的分量为0，因此，IMU 在x向上是解耦的。当IMU 受到侧向的振动激励Λz或者航向的振动激励Λy时，偏移矢量Ψ不为0，也就是系统在y向的线振动与z向上的角振动耦合，在z向上的线振动与y向上的角振动耦合。亦即y向与z向不解耦。则有:

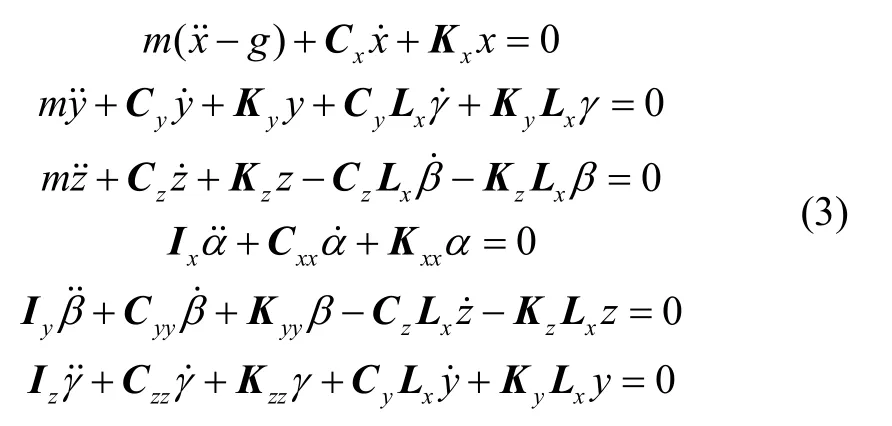
式中L表示隔振器与IMU 质心O之间的距离。假定IMU 台体为边长为2l的正方体，则Ly=Lz=l，又有Lx=ψ，同时假定IMU 为均匀结构，则有:

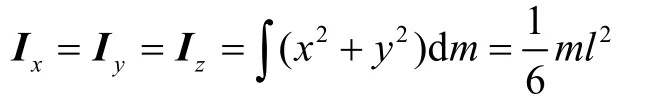
再代入式(2)，则有:

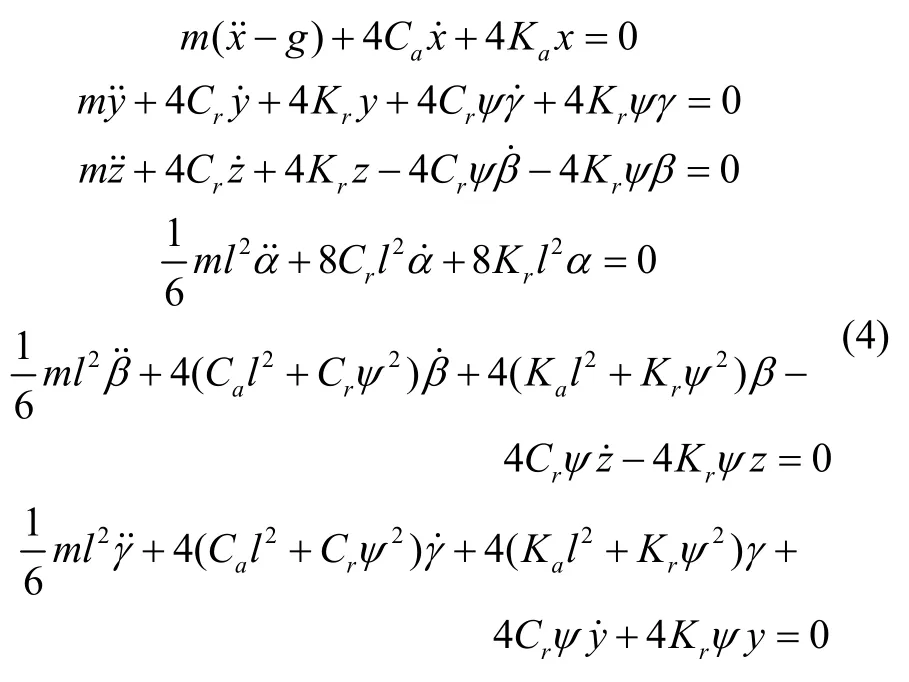
2.3 隔振系统模型分析与计算

我们考虑通过对每个轴向单独施加激励载荷来分析IMU 隔振系统的传递特性。首先对x轴进行分析，在x方向分别施加一个线正弦激励Λx与一个角正弦激励Φx，则有:

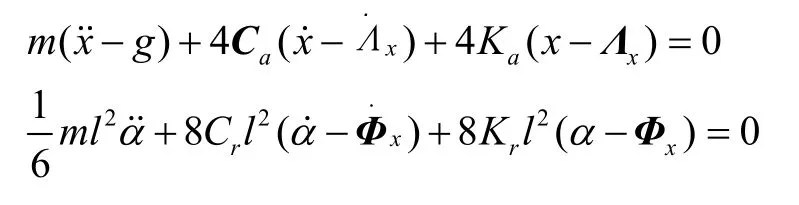
可计算得隔振系统在x方向上的线传递函数hL与角传递函数hA为:

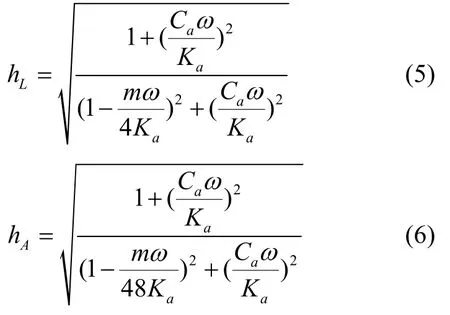
式中ω为圆频率，其他符号意义同前文所述。然后对y轴进行分析，在y方向施加一个线正弦激励Λy，则有:

代入式(7)，并整理为矩阵形式:

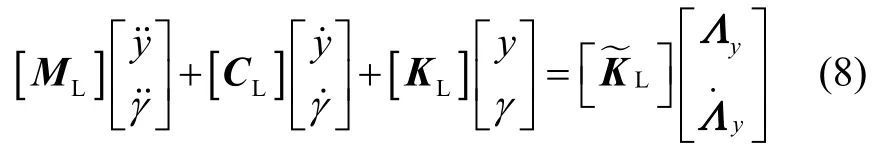
式中:

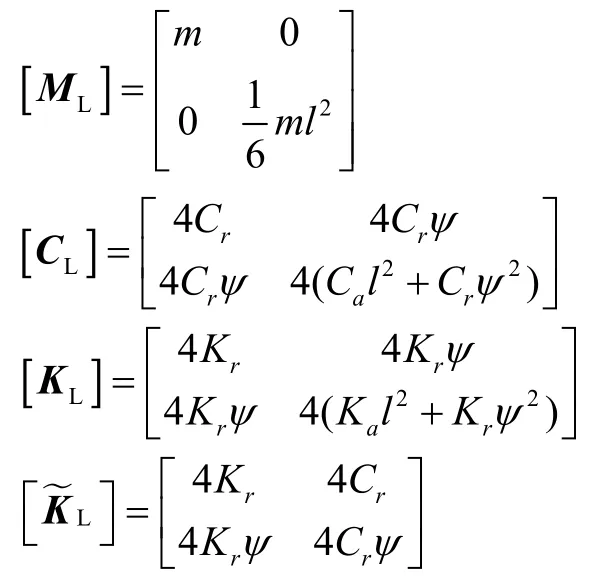
则其阻抗矩阵[ZL]为[15]:

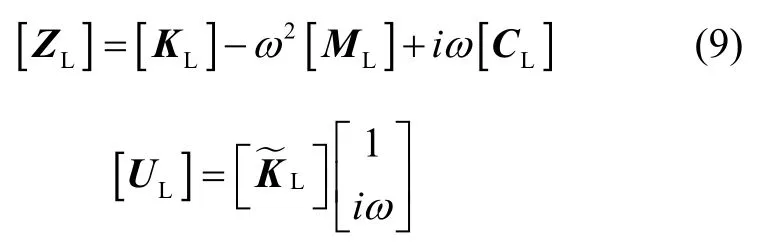
进一步即可得到系统的频响函数[HL]为:

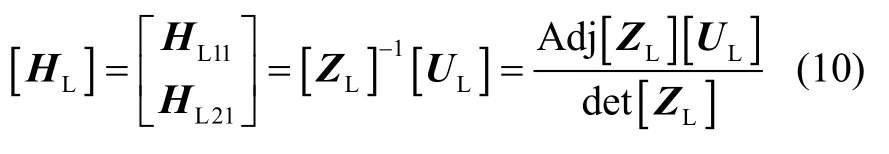
式中:HL11——Λy激励在y方向上的线传递函数；HL21——Λy激励在z方向上的角传递函数；Adj[ZL]——阻抗矩阵ZL的伴随矩阵；det[ZL]——阻抗矩阵ZL的行列式的值。频响函数[HL]算式冗繁，不再展开。

再次对y轴进行分析，在y方向施加一个角正弦激励Φy，则有:

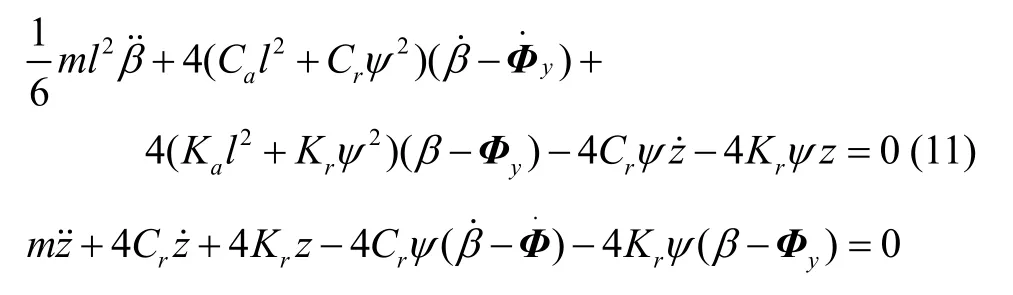
代入式(7)，并整理为矩阵形式:

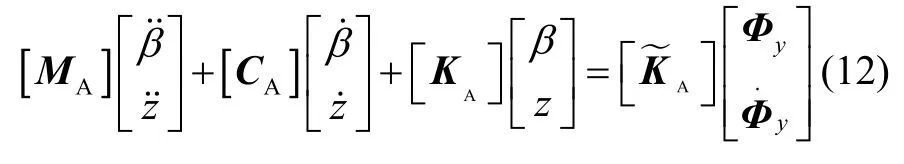
式中:

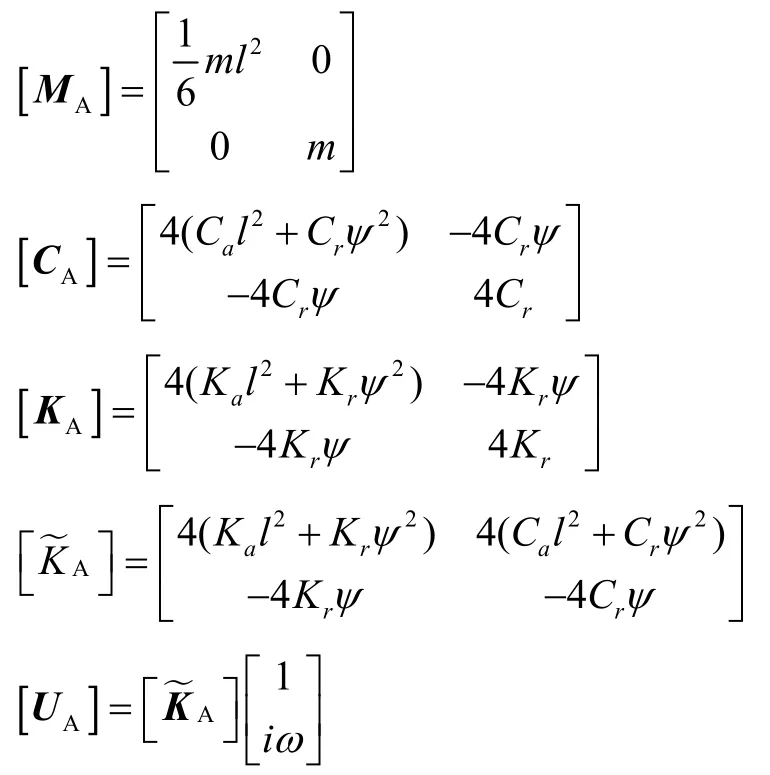
则其阻抗矩阵[ZA]为:

进一步即可得到系统的频响函数[HA]为:

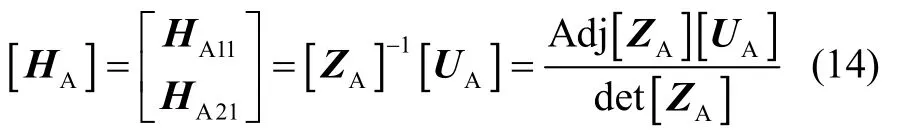
式中:HA11——Φy激励在y方向上的角传递函数；HA21——Φy激励在z方向上的线传递函数，其他符号意义同前文所述。

z轴与y轴振动情况一致，不再赘述。

2.4 模型参数对隔振系统的影响

在x方向上由于不发生耦合，IMU 振动情况与普通单自由度振动系统一致。隔振系统的轴向阻尼Ca与轴向刚度Ka决定着x向线传递率与线共振频率，径向阻尼Cr与径向刚度Kr决定着x向角传递率与角共振频率。

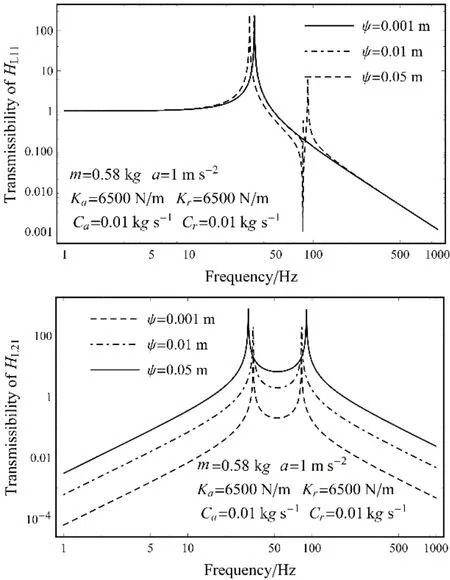
图6 Λy 激励下隔振系统的传递函数曲线Fig.6 The transmissibility curves of the damping system under Λy

在y方向上由于偏移矢量Ψ的存在，使本方向上线振动与z向角振动发生耦合，本方向上角振动与z向线振动发生耦合。IMU 隔振系统轴径向阻尼系数与刚度系数对系统各种振动具有耦合影响。图6为在线振动Λy激励下，偏移矢量Ψ对隔振系统的影响。从图6中可以看出，随着Ψ的减小，耦合作用弱化，角共振频率的影响减小。

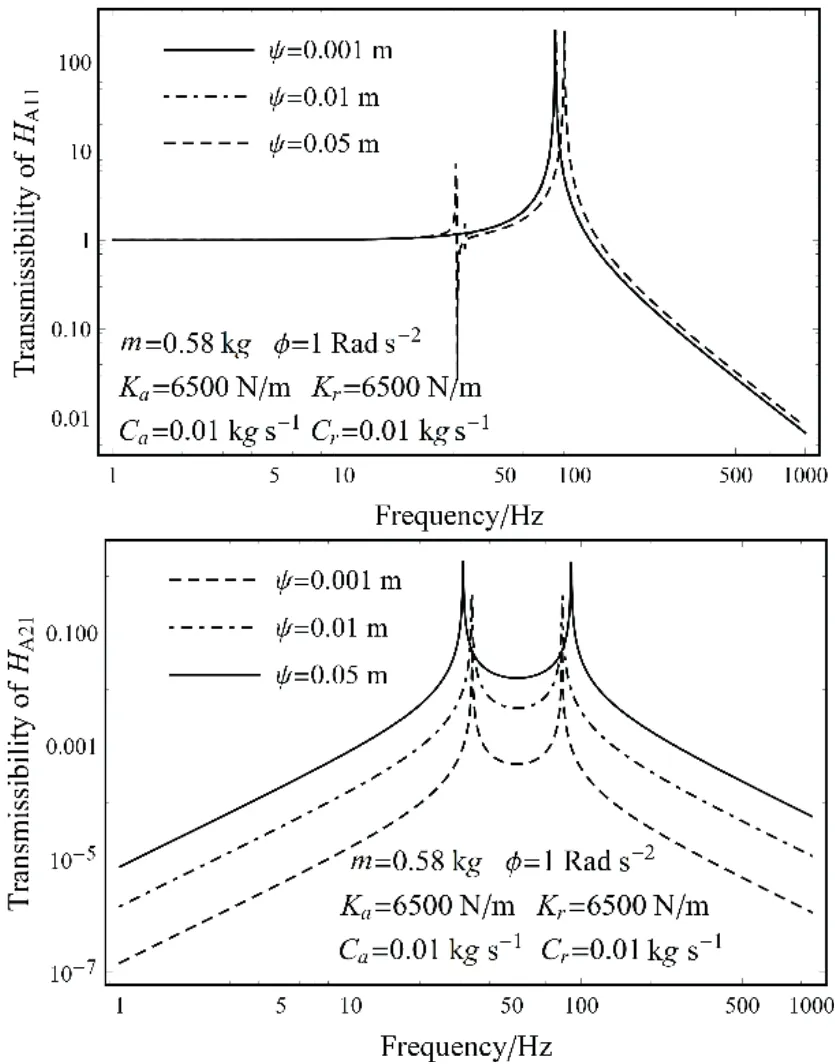
图7 Φy 激励下隔振系统的传递函数曲线Fig.7 The transmissibility curves of the damping system under Φy

与前述类似，当隔振系统受到Φy角激励时，IMU隔振系统轴径向阻尼系数与刚度系数对系统各种振动具有耦合影响。图7为在角振动Φy激励下，偏移矢量Ψ对隔振系统的影响。从图7中可以看出，随着Ψ的减小，耦合作用弱化，线共振频率的影响减小。由于角振动与线振动耦合振动对IMU 的精度会产生影响，需要通过隔振系统的优化设计对振动耦合进行削弱甚至消除。

3 隔振器的设计与优化

3.1 无人机振动环境

本文讨论的某型无人机一阶主桨通过频率为12 Hz。为了避免IMU 与发动机通过频率发生耦合共振，IMU 隔振系统的共振频率应设计在两阶通过频率之间。初步设计隔振系统共振频率为30 Hz。

3.2 隔振系统的分析与计算

本文讨论的IMU 隔振系统如图3所示。四只完全相同的隔振器安装在同一平面上。IMU 质量m=0.58 kg，隔振器之间的安装距离l=120 mm，IMU高度为63 mm，因为安装环境受限，IMU 具有偏移矢量Ψ=[50,0,0] mm，台体质心基本位于IMU 中心点。

隔振系统线共振频率在约30 Hz 左右时，轴向阻尼Ca与径向阻尼Cr对隔振系统耦合振动的影响如图8所示。

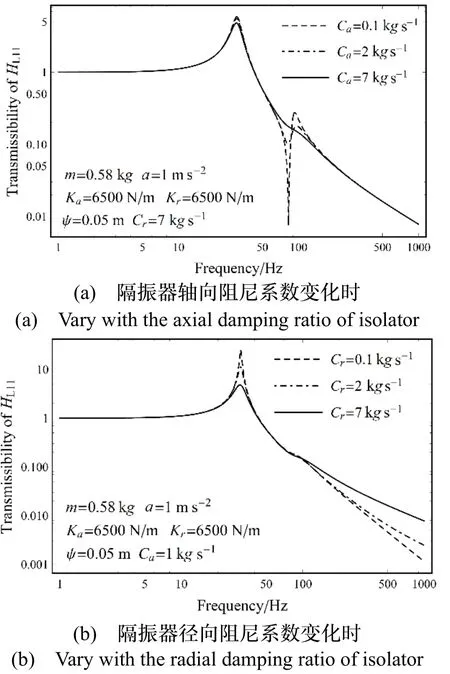
图8 Λy 激励下隔振系统的传递函数曲线Fig.8 The transmissibility curves of the damping system under Λy

可以看出Cr主要贡献是降低了线共振频率点的放大倍数，而Ca则有效地消弭了耦合振动带来的影响，当Ca=7kgs-1时，耦合振动的影响基本上被消除，同时Cr=7kgs-1时，系统的放大倍数为4.8，基本也可满足需求。为了简化计算在初步计算中均令

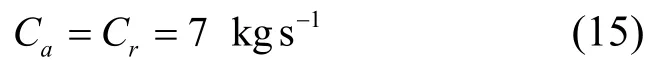
由于x向不与其他方向耦合，首先对其分析。将式(15)代入式(5)中可以计算得:当隔振系统共振频率在30 Hz 时，轴向刚度Ka=5320 N/m。

然后将式(15)与Ka的值代入式(10)中，可以计算得:当共振频率在30 Hz 时，径向刚度Kr=6650 N/m。综合以上讨论，使用前述计算结果绘制隔振系统在轴向x与径向y的传递函数曲线如图9所示。可以看出:虽然隔振系统的传递函数曲线在y向与x向仍然有一些区别，但两个方向线振动曲线可以基本重合且二次峰已经消失。可以认为隔振系统在轴向与径向具有等刚度特性且角振动对线传递函数的影响已基本消除，达到了准解耦状态。

综上，隔振器的轴向刚度与径向刚度之比为:

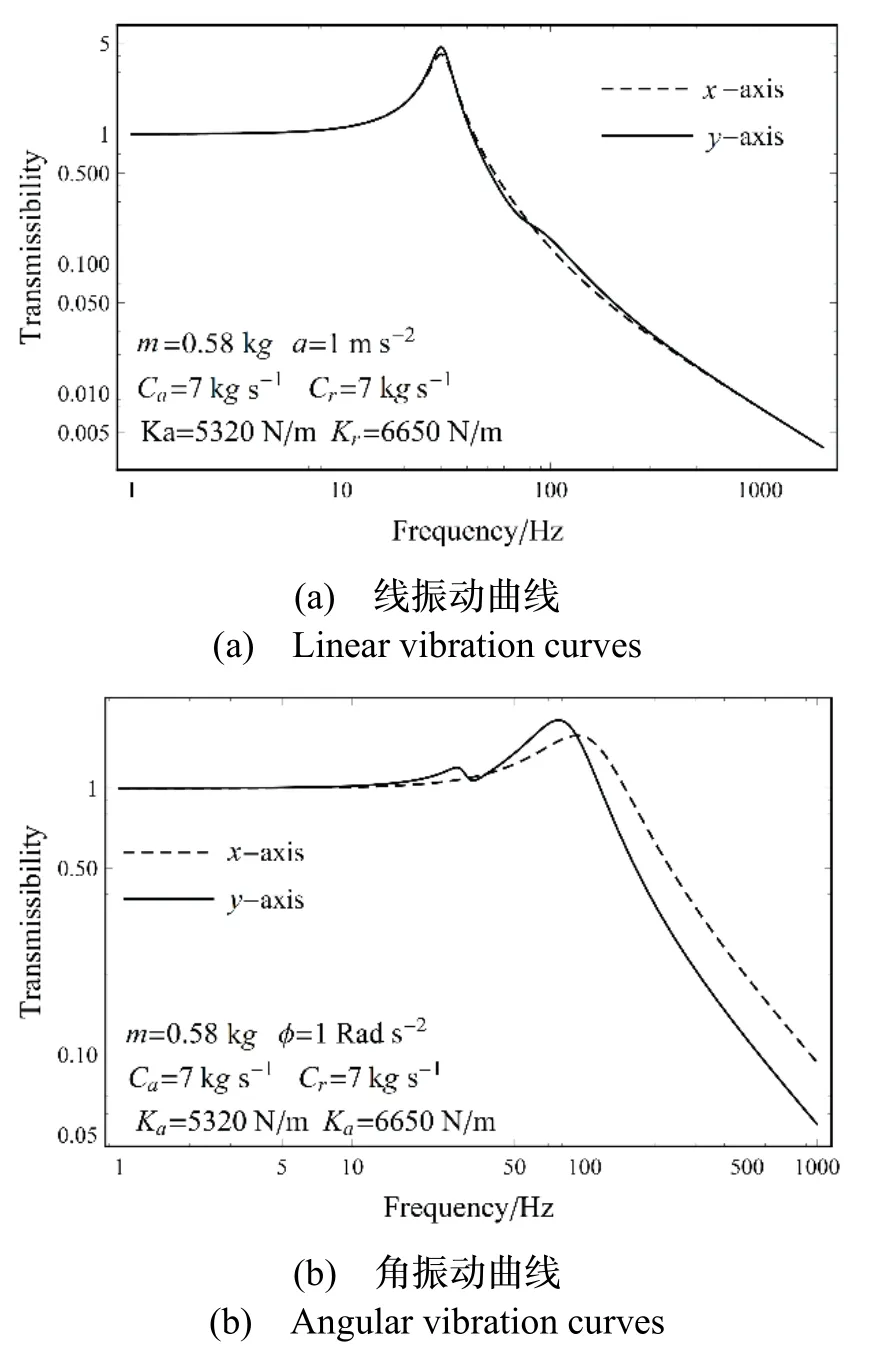
图9 隔振系统传递函数曲线Fig.9 The transmissibility curves of the damping system

3.3 隔振器的设计

由于IMU 在无人机上的安装接口已经确定为两端螺钉安装，且隔振器安装高度不超过13.5 mm，投影直径不超过25 mm。因此设计隔振器如图10所示。

图10 隔振系统的隔振器Fig.10 The isolator of the damping system

将隔振器的阻尼元件假定为各向同性的弹性体材料。使用有限元软件计算并优化阻尼元件尺寸参数，使其轴径刚度比为0.8。结构尺寸参数如表1所示。同时计算得材料参数与计算结果如图11与表2所示。

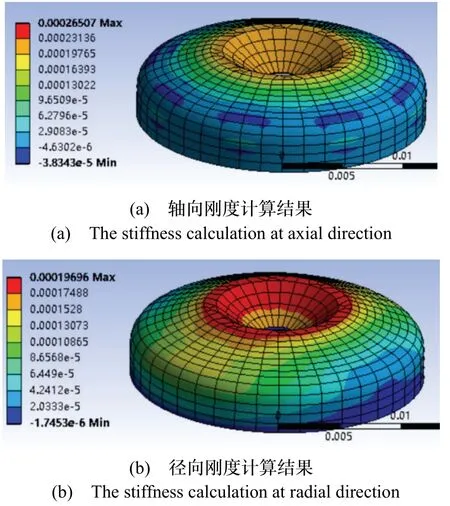
图11 隔振器有限元分析Fig.11 FEA of structure of the isolator

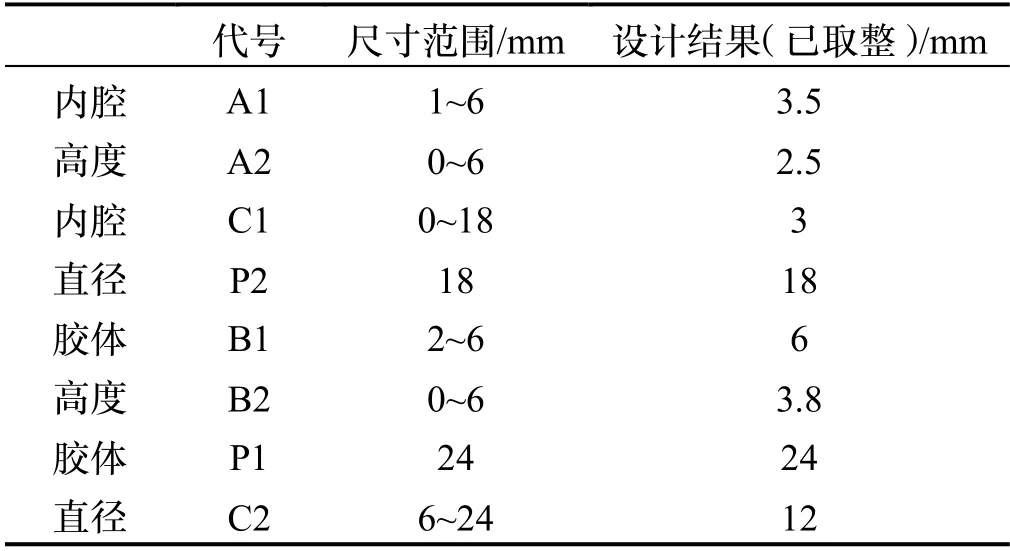
表1 隔振器结构尺寸优化Tab.1 Optimization of the dimensions of the isolator

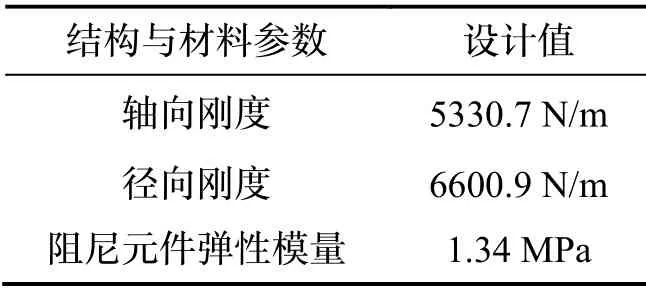
表2 隔振器参数Tab.2 Parameters of the isolator

为了削弱耦合振动带来的影响，前述计算均假定Ca=Cr=7 kgs-1。再代入Ka与Kr，可以计算得阻尼比为:

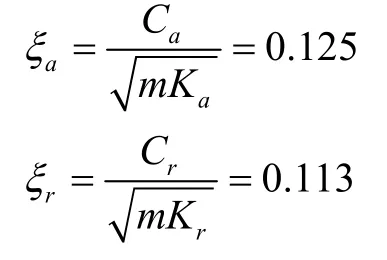
式中ξa，ξr分别为隔振器轴向与径向的阻尼比。亦即隔振器阻尼元件材料的阻尼比ξ大于0.125 即可满足设计要求。

综合以上讨论，隔振系统阻尼元件材料选择牌号为GZG0100Q 的高阻尼硅橡胶材料。材料的弹性模量为1.35 MPa，阻尼比约为0.15，由中国飞机强度研究所生产制造。

4 测试与验证

4.1 试验台测试

将IMU 连同隔振系统安装在振动试验台上，测试隔振系统的传递特性。试验测试照片如图12所示。

图12 振动测试试验照片Fig.12 The picture of the vibration test

4.2 飞行测试

将IMU 连同隔振系统安装在无人机尾部安装接口处，测试IMU 在无人机飞行过程中的工作状态。试验测试照片如图13所示。

图13 飞行测试试验照片Fig.13 The picture of the flight test

4.3 试验结果分析

IMU 隔振系统在振动台上的测试结果如图14所示。图中虚线为理论计算结果，实线为实际振动测试结果。

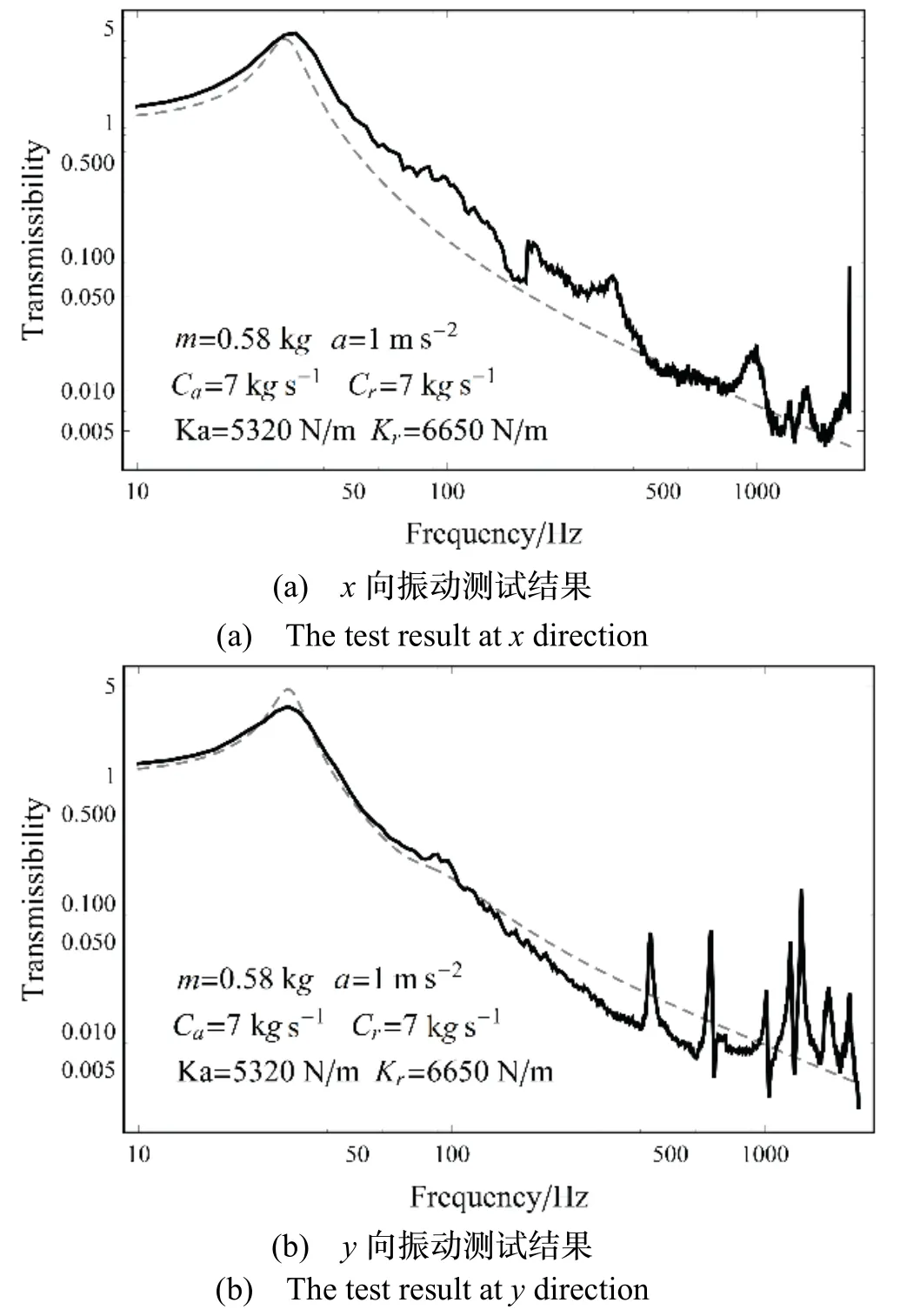
图14 振动测试结果Fig.14 Results of the vibration test

试验结果显示:隔振系统在轴向（x）与侧向（y）均处于准解耦状态。在水平方向上的角振动耦合二次峰已基本上被消除掉。同时轴向与侧向的共振频率基本相同，可以认为系统处于等刚度状态。

无人机飞行过程中的测试结果如图15所示。图中灰色部分为安装IMU 机架上的振动响应，黑色部分为振动隔离后IMU 上的加速度计测得的响应。

图15 飞行测试结果Fig.15 Results of the flight test

可以看出经过振动隔离后，IMU 上的加速度幅值明显减小。其输出数据经过滤波后，峰峰值与隔振前相比减小超过50%。

5 结 论

本文针对无人机非解耦安装环境进行分析，建立基于3-D Voigt 模型的六自由度动力学模型及其动力学方程，对其动力学耦合状态与偏移安装隔振系统进行研究。得出以下结论:

（1）IMU 偏移安装会引起角振动与线振动之间相互耦合，通过隔振系统的设计可以使其达到准解耦状态。理论分析当隔振器的轴径刚度比在0.8 左右，阻尼比在0.125 以上时，角振动所引起的二阶模态可以基本上被消除，且隔振系统处于三向等刚度状态。

（2）依据分析计算设计的隔振系统有效地解决了惯组的振动问题。系统的工作状态与理论分析一致。飞行试验表明经过振动隔离后，IMU 上的加速度幅值明显减小。其输出数据经过滤波后，峰峰值与隔振前相比减小超过50%。该隔振系统有效地削弱了偏移安装环境带来的捷联惯组振动问题，对捷联惯组隔振系统的设计具有指导意义。由于条件所限，隔振系统引起的动态变形并未进行精确计量，需在今后工程实践中进一步验证。