基于Weibull云模型的陀螺输出可靠性分析

2020-10-17秦伟伟邹细刚

中国惯性技术学报 2020年3期

王琪，秦伟伟，沈强，邹细刚，吴艳

（1.中国人民解放军96901 部队，北京 100094；2.火箭军工程大学，西安 710025）

在传统的惯性元件输出可靠性分析方法中，一般需要给出仪器的失效数据[1]，但是对于长寿命陀螺如半球谐振陀螺，在正常条件下很难得到其失效数据，因此研究无失效数据的陀螺输出可靠性分析逐渐成为热点。无失效数据的陀螺可靠性分析具有数据样本少、数据变化规律不明显等特点[2]，传统的基于确定模型的稳定性分析方法不再适用，因此本文提出了一种基于概率统计的陀螺输出可靠性分析方法。

云模型是李德毅院士于1995年在模糊数学和概率统计的基础上提出的定性定量互换模型，云模型综合考虑了模糊性、随机性以及二者之间的关联性，并通过云发生器实现了定性概念与定量数值之间的自然转换[3]。目前云模型主要应用于预测、综合评价、算法改进和知识表示等领域。尽管实验证明，以正态分布和正态隶属函数为基础的云模型对于社会自然科学的各个分支具有普适性[4]，但在一些特定的领域，正态分布和正态隶属函数并不能充分有效地描述被研究对象的特性，因此需要对特定领域特定分布的云模型推理规则进行探讨。

在讨论仪器寿命分布和输出可靠性的时候，Weibull 分布是应用得最为广泛的一种分布形式[5]，它是1993年由Weibull 首次引入的。许多类型的产品，在涉及寿命问题时都广泛提倡运用Weibull 分布，它可用来作为多种类型产品的寿命分布模型。Weibull分布有二参数、三参数两种情形，三参数的比二参数的多一个位置参数，它对应实际中产品寿命的一个下限[6]。另外，其它的寿命分布，如指数分布（单、双参数）、极值分布都为Weibull 分布的特例或变形形式，从而研究它就显得尤为重要。本文推导了Weibull 云模型的推理规则、参数估计方法和Weibull 云发生器构造方法，在此基础上提出了一种基于Weibull 云模型的陀螺输出可靠性分析方法。

1 Weibull 分布及其特征

1.1 Weibull 隶属函数

为了便于推导，本文主要讨论二参数形式的Weibull 分布，三参数形式的Weibull 云模型可以根据二参数形式的直接得到[7]。二参数Weibull 分布的分布函数为[8]:

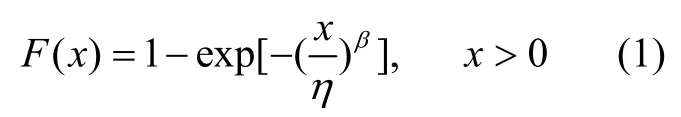
式中，β＞ 0，η＞ 0，β为形状参数，η为尺度参数，记为X～Wei(η,β)。其密度函数为:

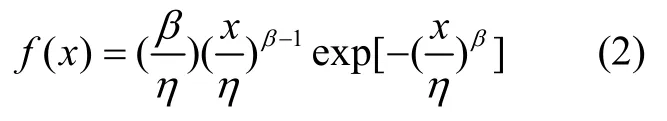
特别的，当β=1时，Weibull 分布就退化为指数分布。

根据Weibull 分布的密度函数，给出Weibull 隶属函数的表达形式为:

式中，c为待确定的常数。

根据隶属度函数的定义可知，隶属度函数的最大值必须等于1[9,10]。由此可以确定常数c的值。

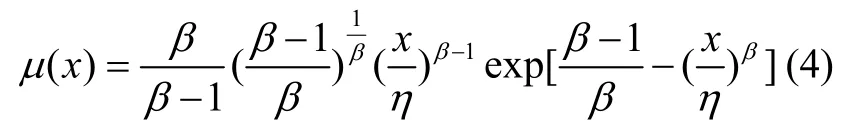
1.2 Weibull 云模型的数字特征

云主要反映了客观世界中定性概念的两种不确定性:模糊性（边界的亦此亦彼性）和随机性（发生的概率），并用语言值表示出这两种不确定性，将两者定量表示出来，构成定性和定量相互的映射[11]。Weibull隶属云中隐含了三次 Weibull 分布规律，记作Wei3(η,β,γ)。其中η、β、γ分别称为Weibull 隶属云的尺度参数、形状参数和超形状参数，是用来表征Weibull 隶属云的三个数字特征值。根据文献[4]中的关于模糊概念“青年”的一组隶属度数据，来说明不同参数对Weibull 隶属度的影响。

（1）尺度参数η:决定了论域中最典型的样本值x0的大小，当x=x0时，其隶属度为1，也就是Weibull隶属云的最高点，不同的η值对Weibull 隶属云的影响如图1所示；

图1 不同的η 值对Weibull 隶属云的影响Fig.1 Effect on Weibull membership cloud of differentη

（2）形状参数β:是概念描述的模糊度，其值越大，该概念能够接受的数值范围就越大，概念就越模糊，不同的β值对Weibull 隶属云的影响如图2所示；

图2 不同的β 值对Weibull 隶属云的影响Fig.2 Effect on Weibull membership cloud of different β

（3）超形状参数γ:反映了同一样本值对模糊概念的隶属度的随机性，其值越小，随机性越大，反应在隶属云图上就是γ越小，隶属云的云层越“厚”，如图3所示。

因此，Weibull 隶属云中隐含的三次Weibull 分布规律为:反映模糊概念亦此亦彼性的隶属云曲线服从Weibull 分布规律；同一样本值对应的不同的隶属度服从 Weibull 分布规律；隶属云厚度变化规律服从Weibull 分布。

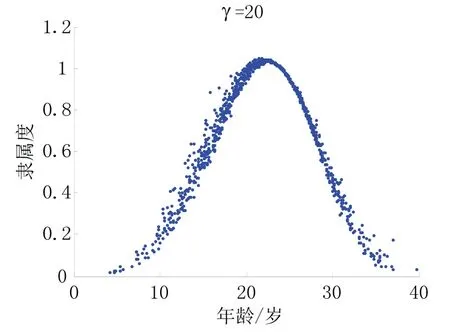
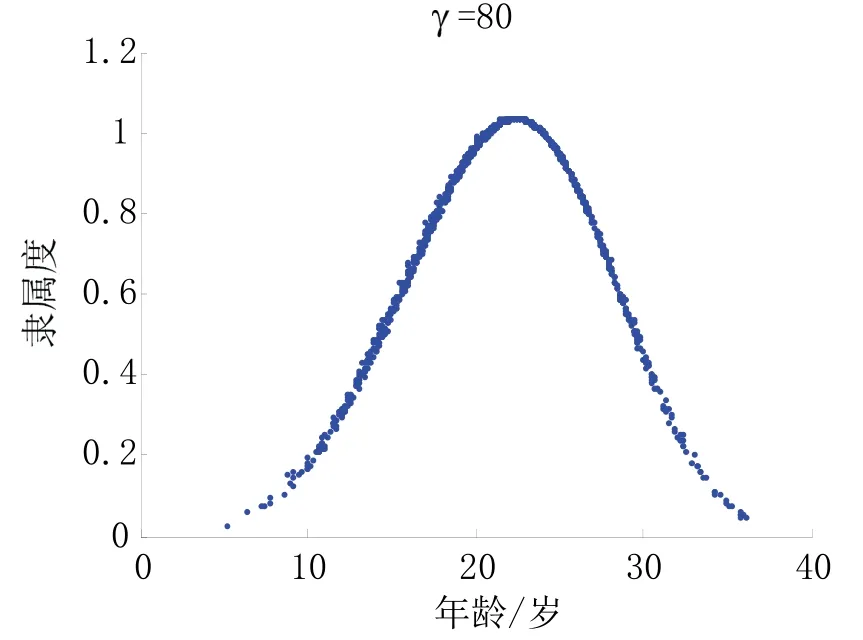
图3 不同的γ 值对Weibull 隶属云的影响Fig.3 Effect on Weibull membership cloud of differentγ

1.3 Weibull 云模型的参数估计

（1）二参数Weibull 分布的参数“矩型”估计

首先给出 Weibull 分布的几个性质[8]。设X～Wei(η,β)，则有:

式中，C为欧拉常数； Γ (⋅)为 Gamma 函数，

对于总体分布X～Wei(η,β)，X1,X2,…,Xn为其一个完全样本，称 lnX1,lnX2,…,lnXn为其对数样本。利用性质1）、2），由矩估计方法有:

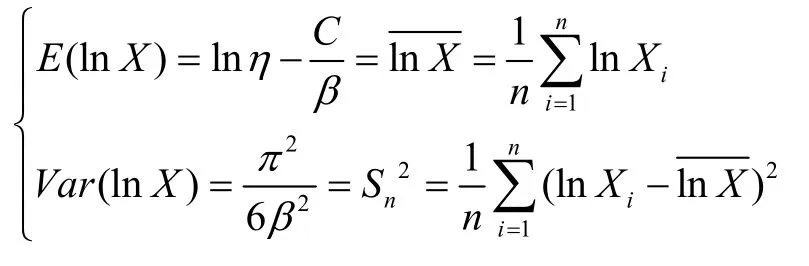
可得:

由式(5)定义的和基于对数样本，所以它们是矩估计的推广，称为“矩型”估计。

（2）Weibull 云模型的参数估计

由前面分析已知，Weibull 隶属云中隐含了三次Weibull 分布规律，分别是:所有样本点服从Weibull分布，即X～Wei(η,β')；形状参数β'服从Weibull 分布，即β' ～Wei(β,γ)；同一样本点的不同隶属度值μi服从Weibull 分布，即μ～Wei(β,γ)。根据前两次Weibull 分布规律就可以估计出Weibull 隶属云的参数(η,β,γ)，具体方法如下:

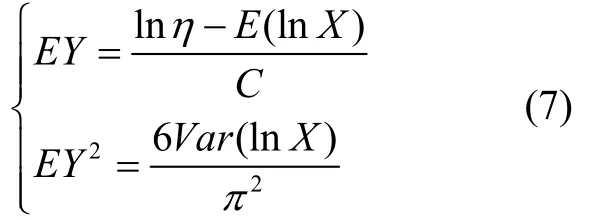
根据Weibull 分布的性质3）、4）可知:

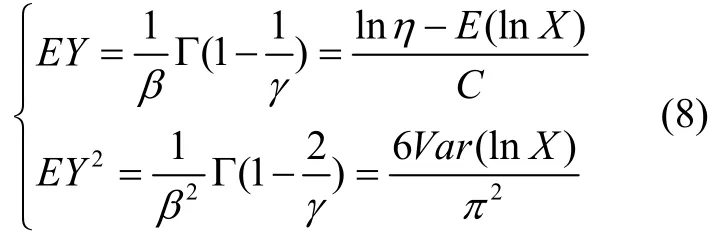
下面给出Gamma 函数的三个性质[12]:

梦想，是人生最不朽的财富。因为梦想，毛泽东才能做到天堑变通途；因为梦想，简·爱才能在卑微的现实中赢得珍贵的爱情；因为梦想，司马迁才能在受宫刑之大辱后坚持创作出了“史家之绝唱，无韵之《离骚》”的伟大著作《史记》。梦想的光芒是如此灿烂辉煌，像远方长明的灯塔，指引着我们在人生的航行中乘风破浪！

联解方程组（8）（9），可得γ的方程式为:

解得γ之后，可得:

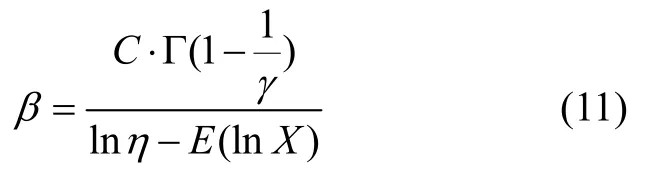
2 Weibull 云模型推理规则

2.1 Weibull 云发生器

为了实现定量数值与定性概念之间的转换,需要构造Weibull 云发生器。根据不同的生成条件，主要有4 种Weibull 云发生器:正向Weibull 云发生器、X条件Weibull 云发生器、Y 条件Weibull 云发生器和逆向Weibull 云发生器[13,14]。下面主要介绍正向Weibull云发生器和逆向Weibull 云发生器。

（1）正向Weibull 云发生器

正向Weibull 云发生器是一个前向的过程，输入3个Weibull云的数字特征(η,β,γ)以及需要生成的云滴数，就可以生成云滴drop(xi,μi)。图4是正向Weibull云发生器的示意图。

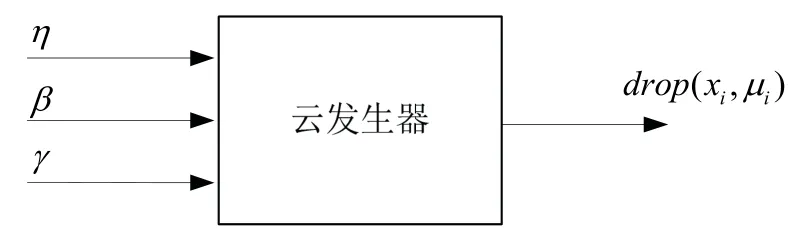
图4 正向Weibull 云发生器Fig.4 Weibull cloud generator

正向Weibull 云发生器的生成算法步骤如下:

1）以β为尺度参数，γ为形状参数，生成一个Weibull 随机数β'=wblrnd(β,γ)；

2）以η为尺度参数，β'为形状参数，生成一个Weibull 随机数xi=wblrnd(η,β')；

3）计算

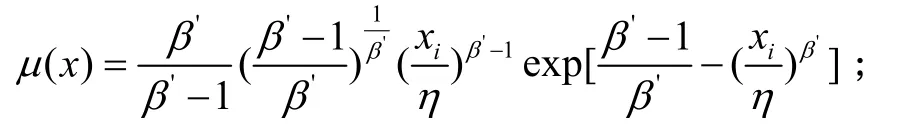
4）重复1）-3）步骤，直至生成需要的n 个云滴xi或表示为drop(xi,μi)。

（2）逆向Weibull 云发生器

逆向Weibull 云发生器是正向Weibull 云发生器的逆过程，它的输入是一定数量的符合Weibull 云模型分布的云滴（只需云滴数量n＞10 就可以较准确地估计参数，且误差小于0.01），输出即为该Weibull 云模型所对应的3 个数字特征(η,β,γ)。图5是逆向Weibull云发生器的示意图。

图5 逆向Weibull 云发生器Fig.5 Weibull backward cloud generator

逆向Weibull 云发生器的生成算法步骤如下:

1）输入样本点xi，根据式（4）计算得到尺度参数η；

2）解方程式（10），得到超形状参数γ；

3）根据式（11）得到形状参数β。

2.2 Weibull 云的统计分析

β'服从以β为尺度参数、γ为形状参数的Weibull分布，β'的概率密度为[17]

x服从以η为尺度参数、β'为形状参数的Weibull分布，x的概率密度为

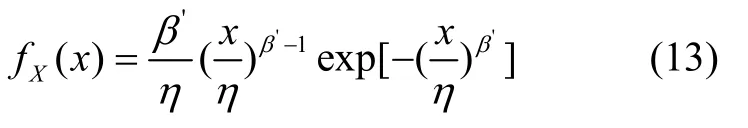
根据式(12)和(13)可得，云滴的概率密度分布函数为

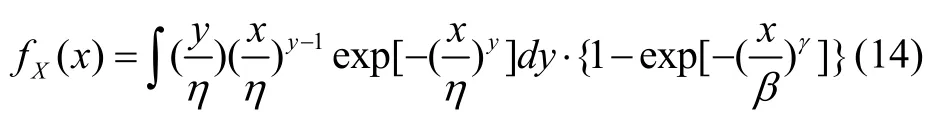
当γ=0时，Weibull 云模型就退化为普通的Weibull 分布。

3 基于Weibull 云模型的输出可靠性分析方法

根据Weibull 云模型的参数估计方法和推理规则，下面给出基于Weibull 云模型的输出可靠性分析方法步骤如下：

1）采集得到分析对象在一定时间内的输出序列；

2）对采集得到的输出进行统计分析，判断其输出分布是否符合Weibull 分布的规律，若符合，则可以用该方法进行输出可靠性分析；

3）利用采集得到的输出数据根据式（4）、（10）和（11）进行参数估计，得到Weibull 预测云模型的三个参数η、β和γ；

4）利用建立的Weibull 预测云模型对分析对象一段时间内的输出进行预测，利用预测数据分析其在一段时间内的输出可靠性。

4 陀螺输出可靠性分析实例

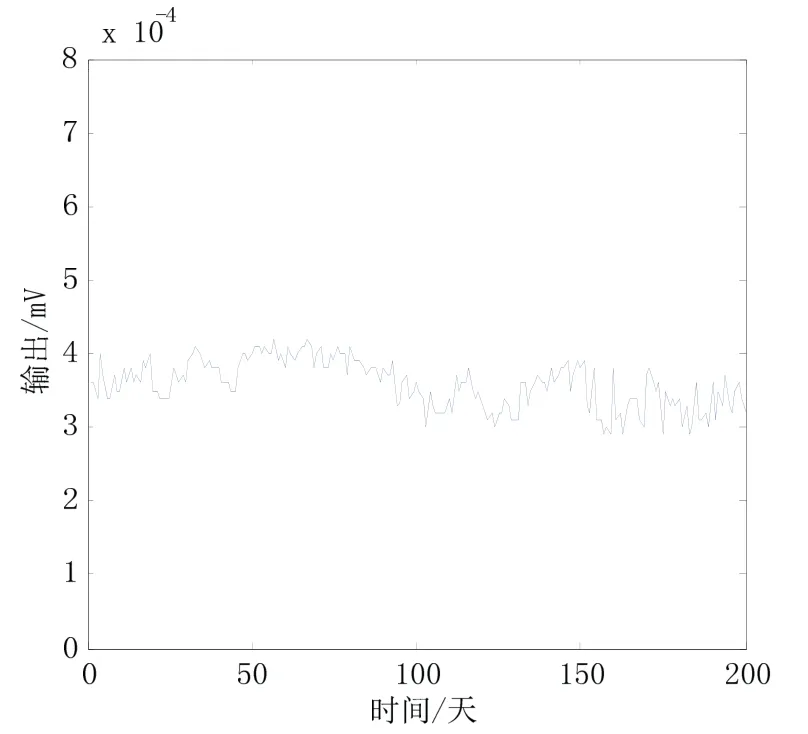
图6 陀螺仪输出历史数据Fig.6 Output data of gyro

为了检验本文提出方法的适用性，现运用某型半球谐振陀螺的输出历史数据进行Weibull 云模型建模，通过建立的Weibull 云模型来分析该半球谐振陀螺的输出可靠性。陀螺仪输出数据如图6所示。

从图6可以看出，陀螺仪的输出数据变化较小，而且没有明显的变化趋势，也没有出现失效数据，常用的可靠性分析方法很难对其进行分析，因此建立其Weibull 云模型，通过模糊数学和概率统计的方法对其输出进行分析。

4.1 Weibull 云的统计分析

为了检验该输出数据的大致分布，画出其频率直方图如图7所示。

图7 输出数据的频率直方图Fig.7 Frequency histogram of output data

从图7中可以看出，输出数据频率的峰值并不是在输出范围的中心，而是略有偏移。因此可知，该输出数据的分布与Weibull 分布更加类似而不是正态分布。因此运用Weibull 云模型来对该输出数据进行分析更加适合。

4.2 Weibull 云模型建模与分析

构造逆向Weibull 云发生器，将陀螺仪输出数据作为输入，可以得到该Weibull 云模型的三个参数:尺度参数η=3.7363×1 0-4，形状参数β=35.6629，超形状参数γ=3.3228。

构造正向Weibull 云发生器，将得到的三个参数输入云发生器中，令n=200，得到200 个云滴的云图如图8所示。

需要指出的是，图8表示的并不是陀螺仪的实际输出，而是200 个预测数据的分布概率[15]。以陀螺仪输出原始数据的阈值，即 [2.9×10-4,4.2×10-4]mV 作为陀螺仪输出的正常范围，当预测数据超出该范围时，认为该陀螺仪不再处于稳定期。考虑到云模型输出的不确定性，共进行了100 次蒙特卡洛仿真，每次预测数据量均为200。仿真结果表明，预测数据超出稳定值范围的平均概率为0.5%，由于测试的采样间隔为1天，可以认为，在200 天的时间内，该陀螺仪处于输出稳定期的概率为99.5%。

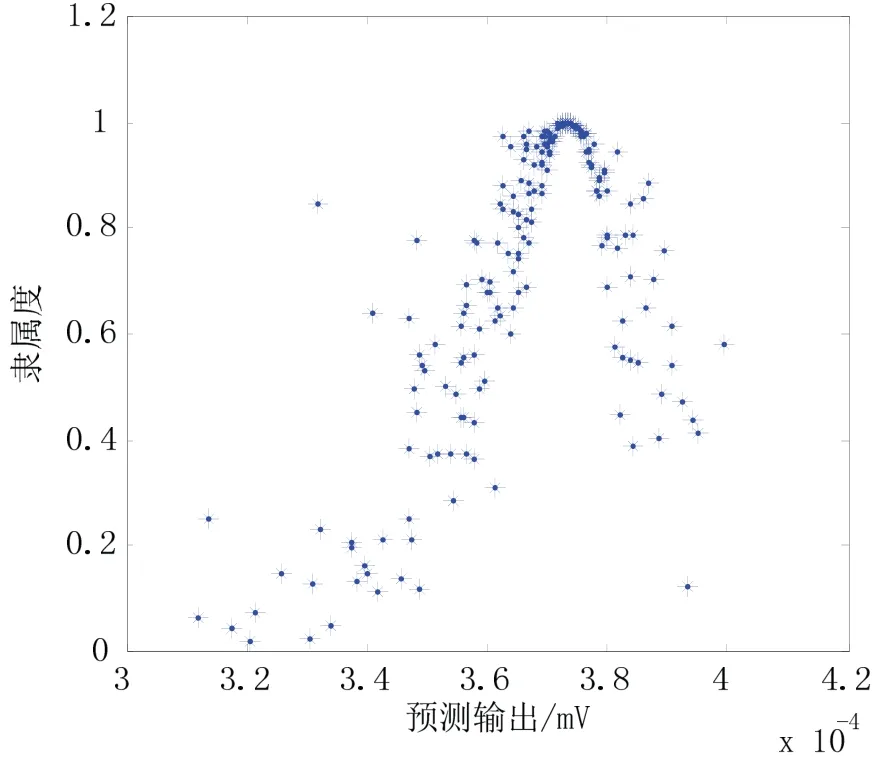
图8 输出的Weibull 隶属云图Fig.8 Figure of output Weibull membership cloud

为了更加准确地描述半球谐振陀螺仪的输出可靠性，引入了统计学上“置信度”的概念。在统计学上，置信度定义为:估计值与总体参数在一定允许的误差范围以内，其相应的概率有多大，这个相应的概率称作置信度。在这里，置信度是指半球谐振陀螺的输出稳定在预定的稳定值范围内的概率，也就是说，该陀螺仪以99.5%的置信度达到200 天的输出可靠期。

有关文献指出，半球谐振陀螺的输出可靠期可以达到3-5年[16]，也就是1095-1825 天左右。经计算可得，该半球谐振陀螺处于3年可靠期的概率为97.29%，处于5年可靠期的概率为95.53%。也就是说，该半球谐振陀螺以97.29%的置信度达到3年的输出可靠期，以95.53%的置信度达到5年的输出可靠期，基本符合实际使用的要求。

从该算例可以看出，Weibull 云模型综合考虑了陀螺仪输出的规律性和不确定性，能够对变化规律不明显的陀螺仪输出进行预测，预测结果符合实际，证明了本文提出方法的适用性。