高中教师资格考试中解析几何试题分析与思考

潘春娟，郑 晨

2010年5月，国务院常务会议审议并通过了《国家中长期教育改革和发展规划纲要（2010—2020年）》（以下简称《规划纲要》）提出：“完善并严格实施教师准入制度，严把教师入口关.国家制定教师资格标准，明确教师任职学历标准和品行要求［1］.同年10月，国务院办公厅发布《关于开展国家教育体制改革试点的通知》（国办发〔2010〕48 号）提出：“开展教师资格考试改革和教师资格定期注册试点，建立中小学新任教师公开招聘制度和办法，探索建立教师退出机制［2］.”2011年9月，教育部率先在浙江、湖北两省开展中小学教师资格考试改革试点工作.2013年8月，《中小学教师资格考试暂行办法》（教师〔2013〕9 号）规定：从2015年开始，我国实行师范生与非师范生教师资格认定方式的并轨［3-4］.我国教师资格的考核与认证工作逐步走向规范之路.师范生在毕业时可自动获取教师资格证的时代一去不复返.从改革发展历程来看，教师资格证书制度的确立逐渐明确了教师资格考试认证程序、考核内容、评价机制等问题，逐步奠定了教师资格考试施行的基础，构建了教师资格考试的现实地位和总体框架，建立科学、公平、权威的国家教师资格考试制度.

通过对相关文献的查阅对比，国内研究者更多比较了美国教师资格考试及教师资格认证与我国教师资格相关政策的差异与启示.从目前的研究成果来看，缺少面向各类学科在具体考试中的研究分析.以数学学科为例，在高中数学教师“数学学科知识与教学能力”的试卷中主要考查学生对大学及高中数学学科知识的掌握和运用，以及数学教学知识的理解情况.多数研究主要对试卷中各个模块进行分析，但是对于某一知识点在考试中的详细分析凤毛麟角. 因此本文选择对2015—2019年10 套真题进行分析，主要针对解析几何部分的内容，通过对学科知识与教学能力试卷整体框架、考查要求的解读，明确命题方向；通过对解析几何试题与题目数量情况、试题分值分布情况分析，通晓知识模块的重点难点；通过对解析几何典型问题的解题分析，明了解题思路和方法；以期能对课程建设与教学改革提供一些启示［5-6］.

1 教师资格考试中解析几何问题的情况分析

1.1 学科知识与教学能力试卷整体框架分析

中学教师资格考试的笔试部分包括“教育知识与能力”“综合素质”“学科知识与教学能力”三门科目.其中“学科知识与教学能力”要求教师必须掌握大学、高中学科知识、课程知识、教学知识、教学技能知识［7］.依托于考试大纲，对4 个模块的题型、分值、总分值、分值比例进行具体分析［8］.试题总体框架如表1所示.

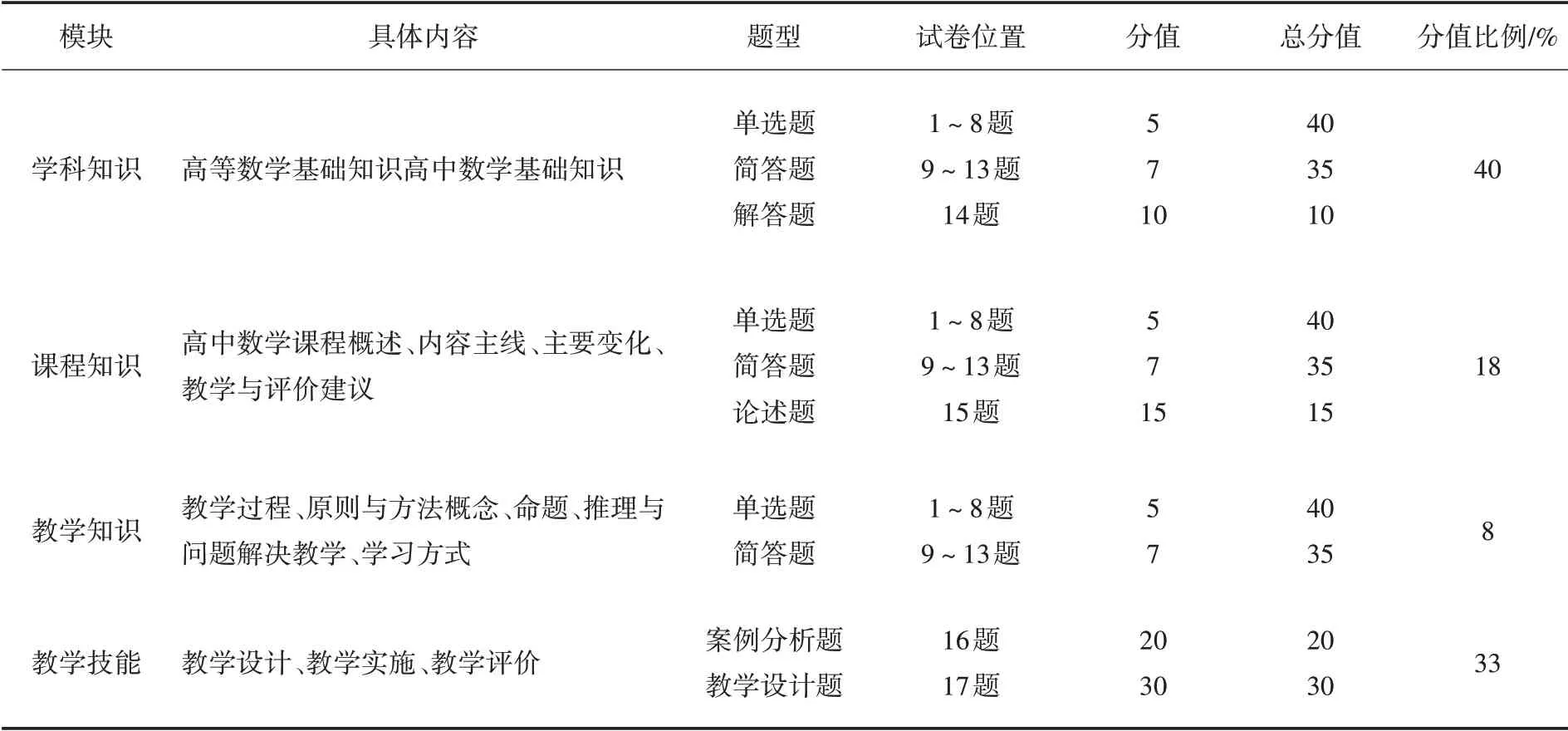
表1 高中数学“学科知识与教学能力”试题总体分析框架

1.2 解析几何考查要求分析

教师资格考试大纲是考试命题的重要依据，也是考生进行备考的重要参考标准.明确考纲要求，分析考查内容，厘清要求中的重点和难点是一项非常重要的任务. 通过对2015—2019年高中数学“学科知识与教学能力”试题的系统分析，发现考纲中解析几何部分主要考查两部分内容，一是高等数学基础知识，其中包括空间坐标与向量、空间平面与直线、曲线及曲线方程三个模块；二是高中数学学科知识，其中包括直线与方程、圆与方程、圆锥曲线3 个模块.具体如表2 所示.

1.3 解析几何题型与题目数量情况分析

在2015—2019年高中数学“学科知识与教学能力”试题中，解析几何总计出题量为32题，（包括2017年下半年14 题的两个问题，2019年上半年和下半年第10 题的两个问题）.其中该部分内容以选择题的形式考查13 次，命题数量为1～2 题；以简答题的形式考查13次，命题数量为1～2 题；以解答题的形式考查3 次，每次命题数量为1 题；以案例分析的形式考查2 次，分别在2018年上半年和2019年下半年各命1 题；以教学设计形式仅考查1次，在2018年下半年命1 题.具体题目数量分布情况如表3 所示.

表2 考纲中解析几何知识点分解表

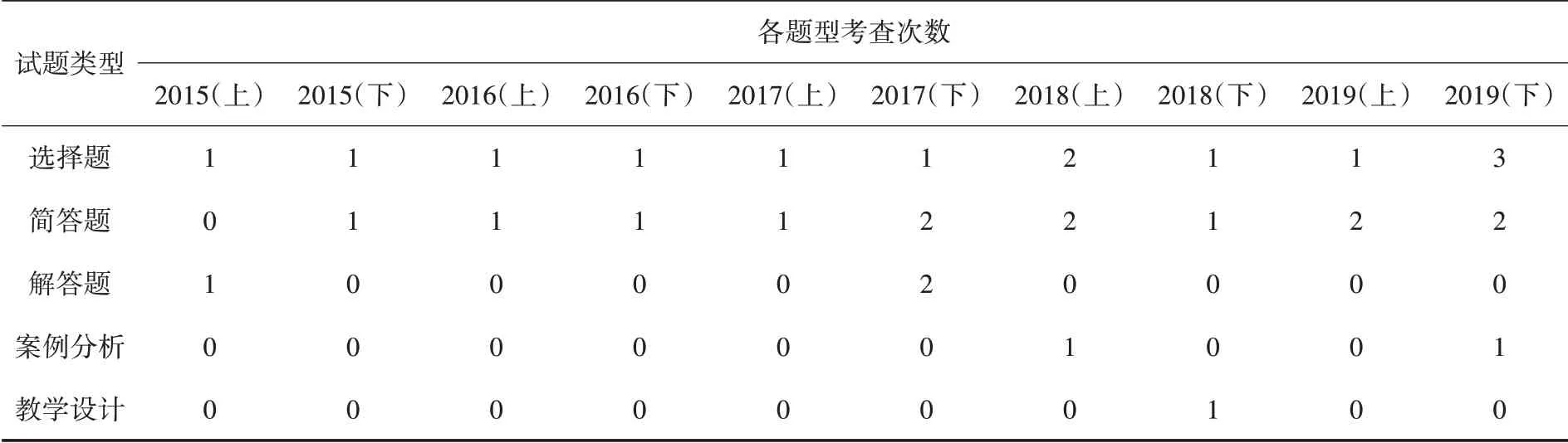
表3 2015—2019年试题各题型考查次数统计表

从考纲分析中可以窥见，解析几何部分内容主要从高等数学角度和高中数学学科知识角度进行命题.在高等数学基础知识三个模块中，空间坐标系与向量共出现5 次，在2019年下半年、2018年下半年、2018年上半年以选择题的形式出现4 次；在2017年下半年以简答题的形式出现1 次.空间平面与直线共命题9 次，在2016年下半年和2019年下半年以选择题的形式出现2 次；在2016—2019年上半年以简答题的形式出现5 次；在2018年上半年以案例分析的形式出现1 次；在2018年下半年以教学设计的形式出现1 次.曲面及曲线方程共命题10 次；在2015年下半年、2016—2018 上半年以选择题的形式出现4 次；在2015—2016 下半年、2018年上半年和2019下半年以简答题的形式出现4 次；在2017年下半年以解答题的形式出现2 次.

高中数学学科知识三个模块中，直线与方程模块在近五年没有命题.圆与方程模块共命题3 次，其中在2019年上半年以选择题的形式出现1 次；在2018年下半年以简答题的形式出现1 次；在2019年下半年以案例分析的形式出现1 次.圆锥曲线模块共命题5次，在2015年上半年和2017年下半年以选择题的形式出现2 次；在2015年上半年以解答题的形式出现1 次、2017年下半年、2019年下半年以简答题的形式出现2 次.具体题型分布情况如表4 所示.

1.4 解析几何试题分值分布情况分析

从高中数学“学科知识与教学能力”考纲要求中可以发现，解析几何内容是教师资格考试必考内容.在2015 上半年选择题考查5分、解答题考查10 分，总计15 分，占试卷总分的10%；2015年下半年至2017年上半年，以及2019年上半年选择题考查5 分、简答题考查7分，总计12 分，约占试卷总分的9%；2017年下半年选择题考查5 分、简答题考查14 分、解答题考查10 分，总计29 分，约占试卷总分的19%；2018年上半年选择题考查10 分、简答题考查14 分、案例分析考查20 分，总计34 分，约占试卷总分的23%；2018年下半年考察选择题5 分、简答题7 分、教学设计30 分，总计42分，约占试卷总分的28%；2019年下半年考察单选题15 分、简答题7 分、案例分析20 分，总计42 分，约占试卷总分的29%.在2015—2019年的十套真题中解析几何部分内容是必考内容，其中单选题总计考查65 分、简答题考查77 分、解答题考查20 分、案例分析考查40 分、教学设计考查30 分.历年真题题型分值统计如表5 所示.

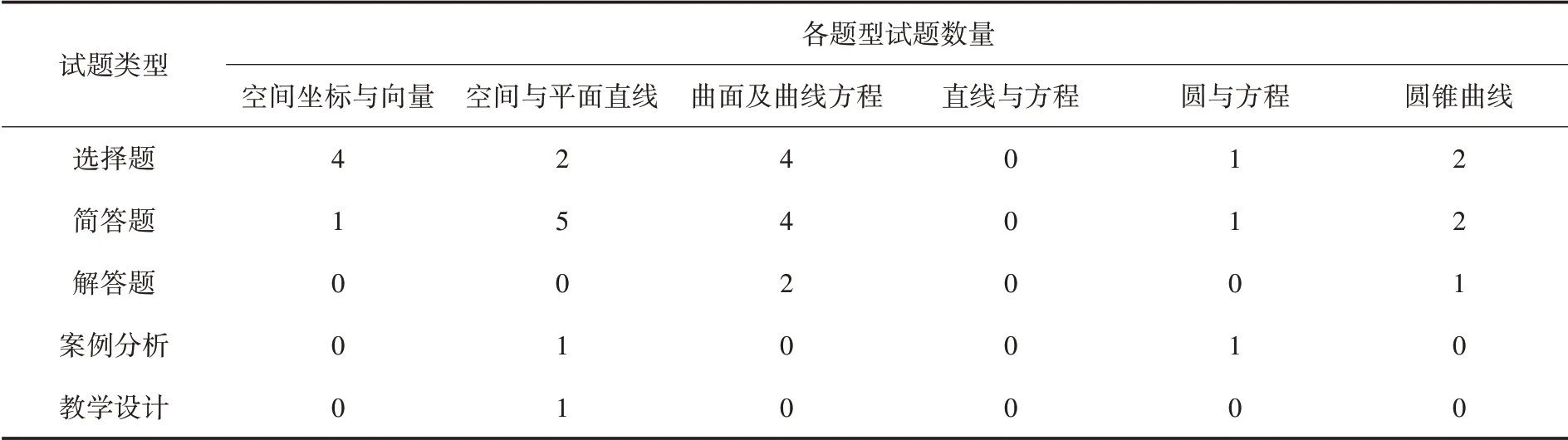
表4 2015—2019年试题各知识点题型与数量统计表

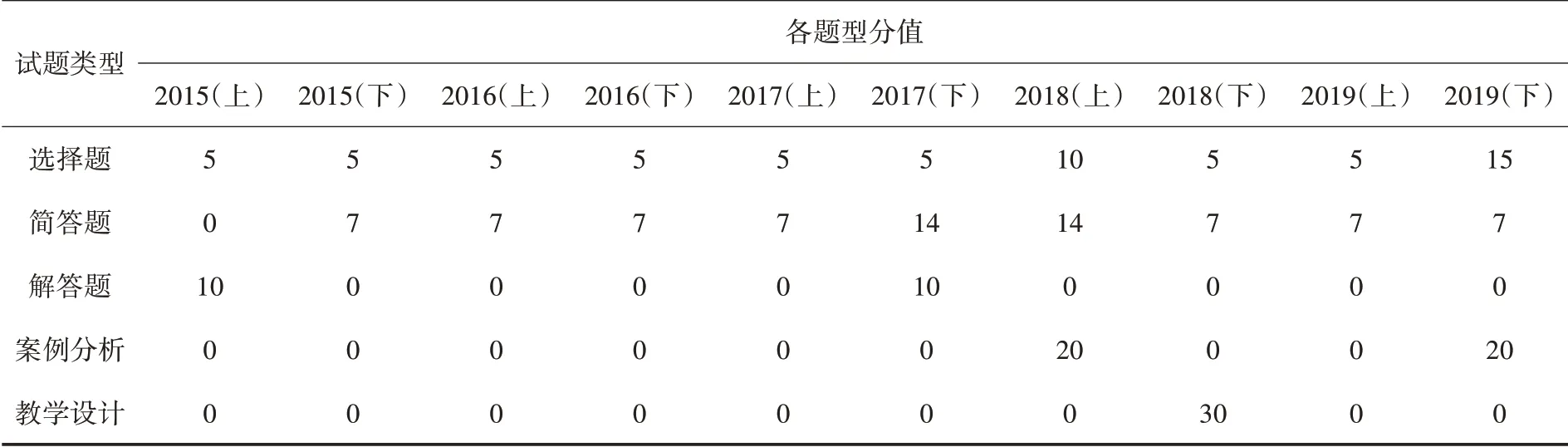
表5 2015—2019年试题题型与分值统计表

在高等数学基础知识3 个模块中，空间坐标系与向量共命题27 分，在2019年下半年、2018年下半年、2018年上半年以选择题的形式命题20 分；在2017年下半年以简答题的形式命题7 分.空间平面与直线共命题88 分，在2016年下半年和2019年下半年以选择题的形式命题10 分；在2016—2019年上半年以简答题的形式出现28 分；在2018年上半年以案例分析的形式命题20 分；在2018年下半年以教学设计的形式命题30 分.曲面及曲线方程共命 题51 分；在2015年 下 半年、2016—2018年上半年以选择题的形式命题20 分；在2015—2016年 下 半 年、2018年 上 半年 和2019年 下 半年以简答题的形式命题21 分；在2017年下半年以解答题的形式命题10 分.

高中数学学科知识3 个模块中直线与方程模块在近5年命题零分.圆与方程模块共命题32 分，其中在2019年上半年以选择题的形式命题5 分；在2018年下半年以简答题的形式命题7 分；在2019年下半年以案例分析的形式命题20 分.圆锥曲线模块共命题34 分，在2015年上半年和2017年下半年以选择题的形式命题10 分；在2015年上半年以解答题的 形 式 命 题10 分、2017年 下 半年、2019年 下半年以简答题的形式命题14 分.历年真题知识点分值分布统计如表6 所示.

2 试卷中解析几何典型问题解题分析

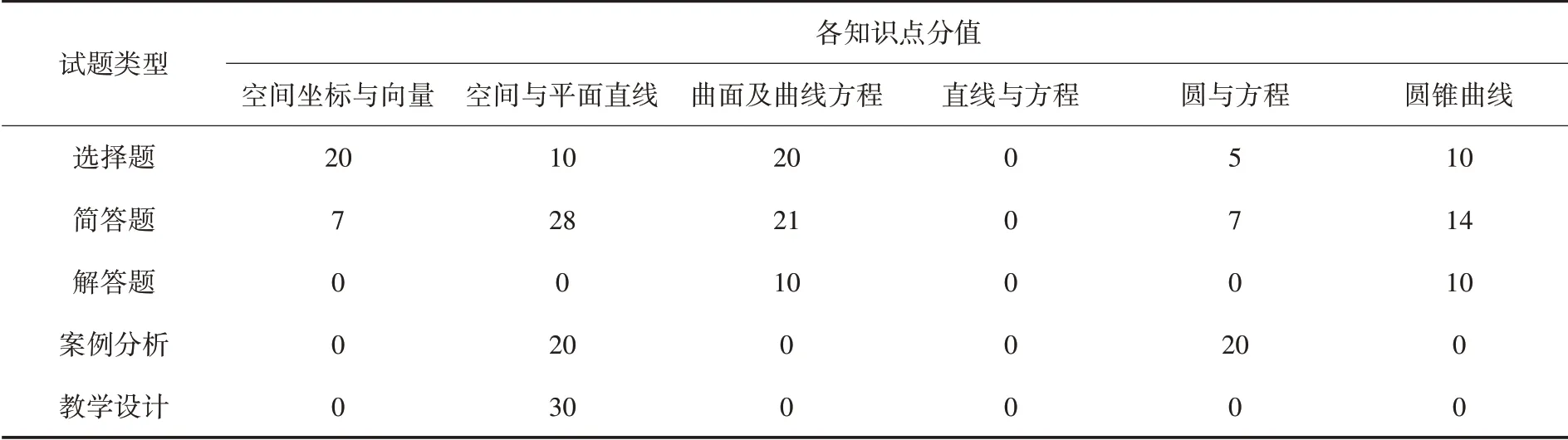
表6 2015—2019年试题各知识点与分值统计表

在对2015—2019年高中数学“学科知识与教学能力”试题量化分析的同时，对试题中的典型问题进行了归纳与总结.由表4、表6可知，解析几何考查最多的是空间平面与直线模块.主要考查了以下几个问题：求解曲面的切平面方程；掌握直线与平面、两平面的位置关系，重点考查通过求法向量的思路来解题的思想.因为求解过程比较繁琐，这些知识点主要借助简答题题型来考查.曲面及曲线方程模块要求学生掌握旋转体体积公式，在求曲面方程时，往往与矩阵知识结合进行命题.空间坐标与向量模块主要考查学生对向量的定义、性质、数量积的理解，以及与实数运算的区别.圆与方程模块要求学生掌握垂径定理、射影定理、相交弦定理，并能够利用几何知识解释代数问题（如借助几何直观来阐述均值不等式等），充分体现了对数形结合的思想的重视.圆锥曲线模块主要考查对椭圆、双曲线、抛物线的概念、定义、性质的掌握，并能区分三者之间的差别.

本文以2004年人教版高中数学教材［9］和吕林根、许子道编著的《解析几何》（第四版）为例［10-11］对具体例题进行分析.

第一种题型是来源于教材中的例题演变.

例1（2019年上半年第10 题）在空间直角坐标系下，试判断直线与直线的位置关系，并求这两条直线间的距离.

本题考查空间两直线的位置关系，该题原型来源于《解析几何》的第三章第七节第3小节例题2.原题是：已知证明此两直线为异面直线，并求l1与l2间的距离与它们的公垂线方程.考题的解题思路是：已知l1方程表达式，先通过二阶行列式来求得方向向量，X1:Y1:= 1:(-1):1，再确定直线上一点，令x= 0，则有y= 0,z= -1，故(x1,y1,z1) =（0,0,-1）是直线上一点，而l2的方向向量为(2,1,1)，而直线过点(1,1,1)，从而有所以两直线为异面直线.而书中原题l1,l2不必用二阶行列式来确定，可直接确定其方向向量v1= {1,-1,0 }，再确定两直线上的点，通过三阶行列式确定两直线异面.

在高中课标中要求学生要掌握平面两直线的位置关系，在高等数学课程《解析几何》中，要求学生掌握空间两直线的位置关系，由此可见大学几何的学习是高中几何内容的延伸.通过对两题的对比，分析两题的异同，让学生体会考题来源于教材常规内容的变形，学生在今后的学习过程中，需要认真解读教材中的例题，尝试对例题进行变式思考、分析，同时，教师在教学中应侧重培养学生对知识的灵活运用，举一反三.

第二种题型来源于教材中的习题演变.

例2（2017年上半年选择题第3 题）母线平行于x轴且通过曲线的柱面方程是（C）.

选项为A.椭圆柱面3x2+ 2z2= 16；B.椭圆柱面x2+ 2y2= 16；C.双曲柱面3y2-z2=16；D.双曲柱面y2- 2z2= 16.

本题考查的是柱面方程，来源于《解析几何》的第四章第一节课后习题第1 题的演变.

本题主要考查学生对柱面、准线、母线概念的理解，以及学生对柱面方程求法的掌握情况.具体要求学生利用已知条件，会求柱面方程表达式.教材中的每一道习题都是经过专家反复斟酌设计的，每道题都有一定的目的和作用，较好地反映了教学目标和学生所应达到的能力要求.因此，教师和学生应从教材入手，钻研教材中的例题与习题，明确出题意图，把握习题与考题之间的内在联系，总结方法，通过变式给学生呈现出全面的数学思考过程，建立完整的认知结构.

第三种题型来源于教材中对性质的理解与掌握.

例3 （2017年下半年简答题13 题）简述向量的数量积运算与实数乘法运算的区别.

本题主要考查学生对向量的数量积运算与实数乘法运算性质的本质认识，同时也考查学生分析问题与解决问题的能力，尤其是学生对向量与实数知识的综合理解能力.向量的数量积运算与实数乘法运算最明显的区别是向量数量积运算不仅涉及向量的长度，还涉及向量的方向，实数的乘法运算满足消去律，向量的数量积则不满足消去律.将两个知识点进行对比，加深对知识的理解，在认知结构中建立知识网络，提升学生的解题水平和思维水平.

3 基于对解析几何试题统计与分析的思考

通过对试题的分析可以发现，在对解析几何试题的考查中侧重对空间平面与直线、曲面及曲面方程的考查，及时分析解析几何试题的考查重点可以明确国家对师资质量的基本要求，也可以对解析几何内容的教学产生导向性的作用.通过对试题的分析可以确定，教师资格考试中解析几何内容的考查点仍可以进一步拓展，这将对今后教师的教学以及学生的学习给予更多的启发.

3.1 试题立足基础，强调知识融合

从考试大纲和本文第二部分对试题考查知识点的分析中可以看到，基础知识的理解与应用是考查的根本所在.考试中对知识点的考查基本遵循以下条件：首先，考查的知识内容严格按照考试大纲规定的范围，绝不超纲.题目的考核意图相当明确，具有层次性；其次，通过考题进一步强化知识主干，重点知识重点考查.从近年试题考查的主干知识模块可以发现：空间平面与直线、曲面及曲线方程仍旧是命题的重中之重.试题中对基础知识的考查既能覆盖全体，又能突出重点，体现对数学思维考查的全面性和针对性.

教师资格考试另一个趋向是注重学科知识的内在联系，强化知识点之间的融合、渗透和灵活应用，并且这种融合以多种形式出现，如同一模块知识点的融合，不同模块知识点的对比，以及结合跨专业、跨学科知识体系的相互融合进行命题，这种命题趋向考查了学生对知识结构理解的贯通性，同时也考查了学生的数学核心素养和综合能力.

3.2 注重贴近实际，密切联系教材

教师资格考试不仅考查学生对于知识的积累是否达到考核要求，同时也以数学知识为桥梁，间接考查学生的迁移能力和应用能力.通过一些贴近生活，密切联系教材的考题，实现对学生运用数学知识分析和解决问题能力的考察，从而进一步引导学生关注社会、生活实践，培养学生实际应用的能力.同时通过对近年的试题分析发现，部分题目能在教材上找到“影子”，考核的知识点基于课本，形式与难度又高于课本.因此，在大学解析几何内容的教学中，要重视对教材内容进行进一步挖掘，教师在教学过程中可以借助教材中的题目进行改编，对习题再次加工与重新打磨，提升学生的分析能力与解题能力.从试题考核题型与题量来看，对于该部分内容试题的考核比重不会发生明显变化，但对学生探究能力的考查力度会逐渐加大.

3.3 夯实教师教学基本功，突破教学难点

教师在日常教学中可以结合学科知识与教学能力考试要求，有针对性的调整教学设计，同时，要结合高中数学课程标准，建立高中数学内容与高等数学内容之间的知识整合.教学应从教材出发，结合考试中的考点，突出培养学生的思维能力和学科素养.从教材出发，重视使用教材，培养学生的思维能力和运算能力，加深学生对概念的发生、发展过程的理解，建构数学模型.对于习题课的教学，应梳理相关知识体系，分析知识点间内在联系，总结规律.真正落实基本知识、基本技能、基本思想.解析几何教学的关键在于教师要引导学生在变化的考查知识现象中研究不变的知识本质，从不变的知识本质中探究变化的规律.运动变化思想、回归定义思想、数形结合思想、化坐标思想、优选直线方程思想是解析几何的本质规律，把握这些不变的本质规律就能以不变应万变，让教学走出困境，为教学减负增效.

3.4 提高知识迁移能力，培养发散思维

解析几何问题是教师资格考试的必考点，更是高中数学教学中的一个重要内容.夯实基础知识，是培养学生迁移能力的基础.因此要求教师要在对其性质、概念、定义内容进行精确理解和掌握的基础上，善于从生活中寻找现实案例，并将其巧妙地融合到具体教学中.从习题中培养学生的发散思维能力，为学生选择典型的习题并且在不断的练习过程中探索和总结各类题型的特点，通过探索使所得的知识与技能进一步得到巩固和提高.当学生面对解析几何知识与统计、概率等知识结合出题时，能够变式地、综合地思考问题，准确分辨考查知识点，促进学生对解析几何知识点的全面掌握.因此，教师在日常教学中要重视学生主体地位，遵循学生的认知规律，做好详尽的教学计划，不断探索行之有效的教学方法，更全面、细致地进行教学设计，完成教学任务.