基于Mathematica 的函数连续性的教学实践研究
2020-10-16高忠社
高忠社
在高等数学教学中使用数学软件Mathematica,可以实现和验证一些抽象的问题,有助于学生深刻理解和掌握这些抽象的数学知识[1-3].笔者从教学实践中发现,学生对函数的连续性的定义较长时间无法理解,而函数的连续性是高等数学中的一个重要概念,也是学生在学习数列极限、函数极限之后,需要很好掌握的重要概念,函数连续性概念的掌握情况,对后续导数、积分、函数项级数等知识点的学习都会产生较大影响[4-7].
由于学生对于任意性、极限的过程等问题没有完全理解,因而在学习过程中会产生一系列的疑问,为什么函数的连续性要取决于函数在任意一个点上的连续?为什么函数y=f(x) 在任意点x0满足了或时,函数在该点就连续等等.学生很难理解这些抽象的概念,学生这时可以借助Mathematica 软件的图像功能,尽可能的通过实例直观分析函数的极限过程,以及函数值的情况,通过这种直观的分析帮助学生理解函数的连续性[8-9].
因此,在教学实践中对于一些抽象的概念的讲授中,可以适当使用数学软件来直观分析实例,帮助学生理解这些抽象概念.下面将对一元函数的连续性、左连续、右连续、间断点;二元函数的连续性等问题分别使用数学软件Mathematica 结合实例进行分析.
1 一元函数的连续性与Mathematica
高等数学中对于连续性的引入是这样的,“自然界中有许多现象,如气温的变化、河水的流动、植物的生长等等,都是连续变化的.这种现象在函数关系上的反映,就是函数的连续性”,但是学生对这样的描述难以理解.而对于函数在一点的连续性是按如下方式进行定义的.
1.1 函数在一点连续的定义
定义1[1-2]函数y=f(x)在点x0的某一邻域内有定义,如果
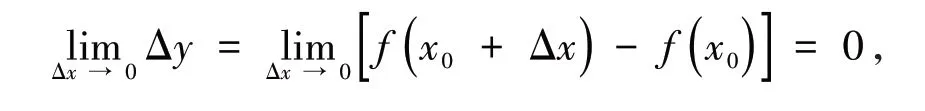
这是一个抽象的概念,即“当自变量的增量趋于零时,函数值的增量也趋于零”,则函数在点x0处连续.由于学生对函数极限定义还没有很好掌握,而函数的连续性需要使用函数的极限来定义,使得有些学生觉得难以理解,进而对这类抽象性的概念的学习慢慢的失去了信心.如果在教学实践中通过一些直观的实例帮助学生理解这种概念,学生将会产生学习兴趣.
如果引入适当的例子,使用数学软件Mathematica 进行适当的直观性分析,会取得更好的教学效果,如:
例1 验证函数y= 4x2+ 3x+ 1 在x0= 0的连续性.
分析:学生在中学阶段对该函数已经很熟悉,函数的图像为抛物线,是一条连续曲线(见图1),因此在x0= 0 处是连续的.使用定义1 验证.
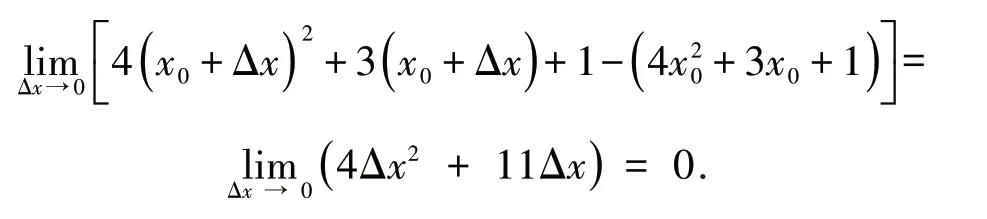
故函数y在x0= 0 处连续.
Mathematica 命令如下:


图1 4Δx2 + 11Δx →0(Δx →0 )的图像
从 图1 可 以 看 出,当Δx→0 时,4Δx2+11Δx→0,满足定义,因此函数在x0= 0 处连续.
通过对图像的直观表示,加深了学生对于函数连续性概念的理解,同时也加强了对函数极限定义的理解.
定义1 又可表述如下:设函数y=f( )x在点x0的某一邻域内有定义,如果则称在点x0连续.
1.2 左连续及右连续概念的分析
在高等数学教材中同样定义了函数左、右连续的问题,定义方式如下:
利用左、右连续的定义对例1 继续进行讨论,通过Mathematica 作图,观察发现,函数在x0= 1 处的极限,当x→1+,x→1-时,函数的极限即函数在x0= 1 处连续.函数图像如图2 所示.
Mathematica 命令如下:

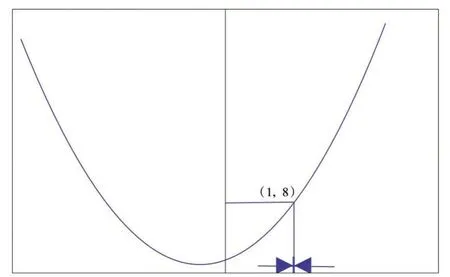
图2 函数4x2 + 3x + 1 极限值等于函数值的图像
1.3 函数在区间上连续的定义
如果函数f(x)在开区间(a,b)内每一点都连续,则称f(x)在开区间(a,b)内连续;如果函数f(x)在开区间(a,b)内连续,在点a右连续,在点b左连续,则称函数f(x)在闭区间[a,b]上连续.
上面的这些定义都是用极限定义的,对于学生来说仍然是比较抽象的.因此,教学实践中需要一些具体实例来分析这些抽象的问题,下面将通过具体实例来分析函数在整个定义域区间上的连续性.
Mathematica 命令如下:
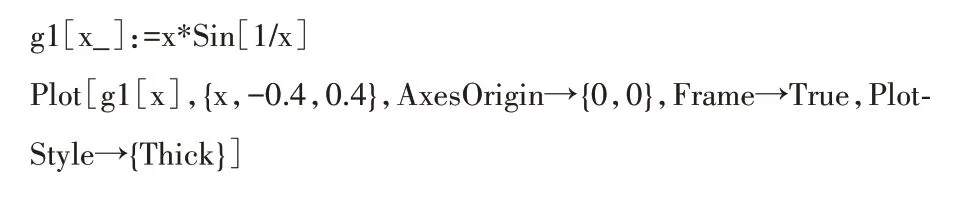
图3 函数f(x)在x=0 处连续的图像
2 函数的间断点
①在x=x0没有定义;
②虽在x=x0有定义,但不存在;
③虽在x=x0有定义,且存在,但
间断点x0通常分为两类. 如果左极限及右极限都存在,那么x0称为函数的第一类间断点.包括可去间断点和跳跃间断点.当时为可去间断点,当时为跳跃间断点.如果左极限
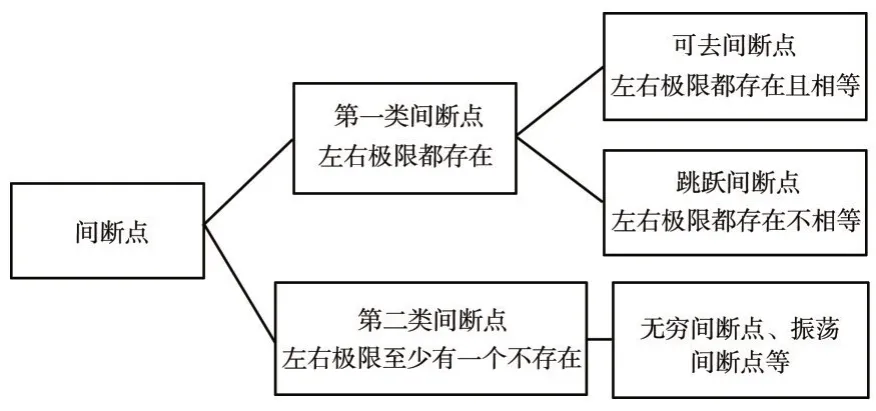
图4 间断的分类
对于这样抽象的定义,需要给予具体的详细的实例,图文并茂的来解释这些不同的间断点,使用数学软件Mathematica 配合教学实践,通过图像来分析.
例3 验证x= 0 为函数的可去间断点.
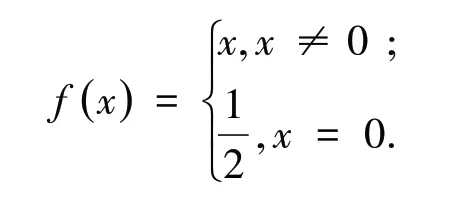
Mathematica 命令如下:

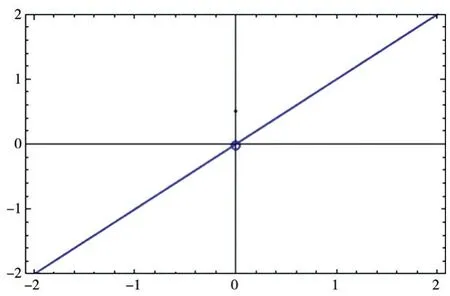
图5 函数f(x ) 在[-2,2]的图像
从图5 可以看出,函数y=f(x)在x= 0处,左、右极限都存在且相等,但是极限值不等于函数值.根据定义,该点为可去间断点.使用Mathematica 作图,使得学生更为直观的发现可去间断点的特征,更深刻的理解可去间断点的定义.
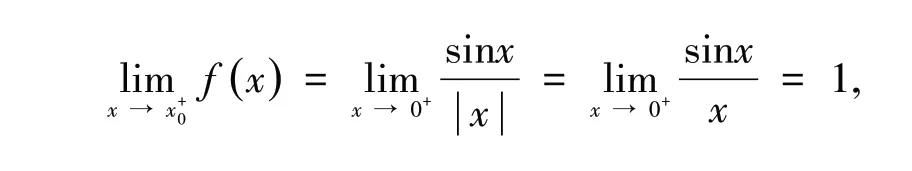
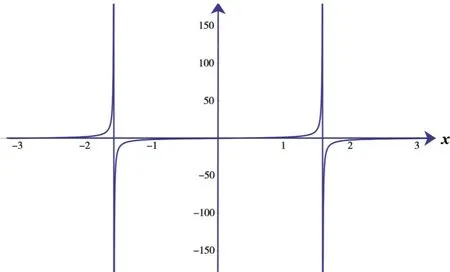
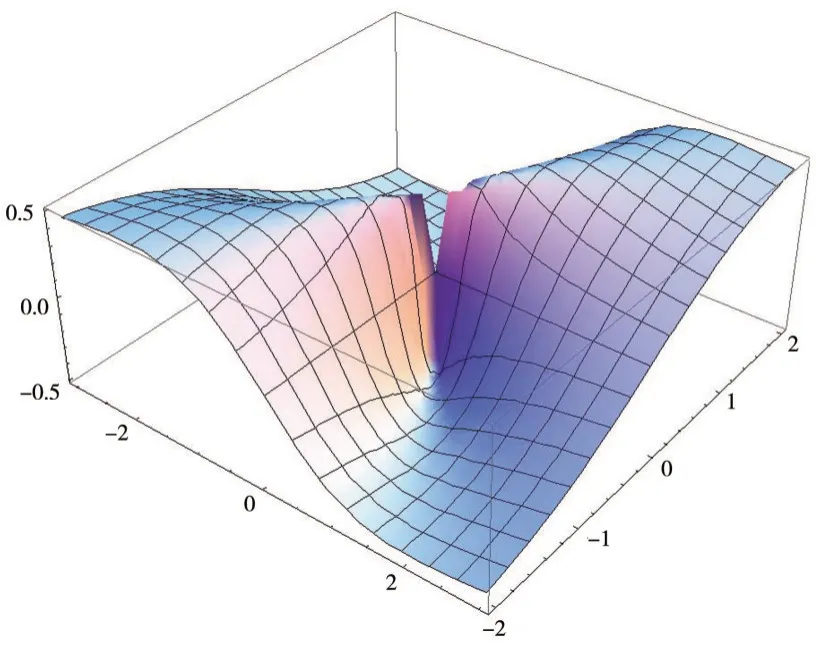
在x 使用数学软件Mathematica 绘图图像如图6 所示. Mathematica 命令如下: 图6 函数在x0 = 0 邻域内的图像 例5 讨论正切函数y= tanx在处的间断点类型. 解 因为y= tanx在处无定义,且所以为函数tanx的无穷间断点.函数图像如图7 所示. Mathematica 命令如下: 图7 函数y = tanx 在[-π,π]的图像 从图7 可以看出,函数y= tanx在处及的点处都趋于无穷,因此,这些点均为函数的无穷间断点.使用数学软件Mathematica 作图,观察该图像,就能使得学生更为深刻的理解无穷间断点的定义. Mathematica 命令如下: 图8 函数在[-0.3,0.3]的图像 二元函数z=f(x,y),(x,y) ∈D⊂R2的图像是空间曲面或曲线,对于空间想象能力不强的学生来说,对于这些空间图像的理解有一定的困难,有时需要使用教学辅助手段.由于教具已经慢慢淡出了教学过程,教学辅助手段需要借助于数学软件、多媒体等手段来实现,帮助学生理解一些抽象的,或难以想象的曲面相交所产生的图像.文献[4]中介绍了使用数学软件Mathematica 分析二元函数的连续性的方法,下面将分析这些方法在教学实践中如何具体的应用,以及如何取得更好的教学效果. 在高等数学教材中,二元函数的连续性定义和一元函数类似. 定 义2[1-2]设 二元函数z=f(x,y),(x,y) ∈D⊂R2,P0定义为D⊂R2的聚点,且P0∈D.如果则 称 函 数z=f(x,y)在点P0(x0,y0)连续. 如果函数z=f(x,y) 在D的每一点都连续,那么就称函数z=f(x,y)在D上连续,或者称z=f(x,y)是D上的连续函数. 定义3[1-2]设函数z=f(x,y)的定义域为D,P0(x0,y0)是D的聚点.如果函数P0(x0,y0)在点P0(x0,y0) 不连续,则称P0(x0,y0) 为函数f(x,y)的间断点. 例 7[1-2]讨论函数f(x,y) = 在(0,0)的间断点类型. 解 易知函数f(x,y) 的定义域D= R2,(0,0) 是D的 聚 点.当(x,y) →(0,0) 时,函 数f(x,y)的极限不存在,所以点O(0,0)是该函数的一个间断点. 当在教材中遇到这样的问题,有些学生很难理解,无法想象该图像是什么样的.如果在教学实践中能够给出该函数所表示的图像,给出函数在(0,0)的形状,能更好的帮助学生理解该问题;利用Mathematica 的Plot3D命令绘制出图像,图像如图9 所示. Mathematica 命令如下: 图9 函数z = f(x,y)在[-2,2]×[-2,2]的图像 从图9 可以看出,函数z=f(x,y)表示的曲面在点(0,0)出现“裂口”,而且上下陡峭,意味着,即使在(0,0)补上f(0,0) = 0,仍然不足以弥补曲面上这个“大裂口”,从直观上,函数f(x,y) 在点(0,0)处不连续,曲面在点(0,0)附近即出现了“山脊”和“山堑”,当动点(x,y)沿“山脊”路径y=x趋于定点(0,0)时,极限当动点(x,y)沿“ 山 堑”路 径y= -x趋 于 定 点(0,0)时,两者不相等,则极限不存在,由函数连续的定义可知,函数f(x,y)在点(0,0)处不连续.由例7可以看出,用图像法判定和讨论二元函数z=f(x,y)的连续性,直观而真实,能透过现象直达本质,具有纯理论的抽象研讨无法媲美的优点,但也有一定的局限性[4]. 对于二元函数z=f(x,y)的图形空间的曲线或曲面,在实践教学中很难使得学生理解其中的一些抽象的性质、图像等,如果在实践教学中借助于多媒体技术,数学软件等,给予学生展示其图像,曲面的切平面、法线,曲线的切线、法平面以及多个曲面相交产生的空间图像,可以更好的帮助学生理解该函数的性质,如连续性及一些抽象的概念. 文中结合一元函数、二元函数的连续性定义、一元函数的各类间断点,结合笔者自己的一线教学实践经验,学生在学习这些知识点中遇到的困难、疑惑,分别对间断点的每一种情况,给出了具体实例,结合Mathematica 作图分析,且给出了相应的Mathematica 作图命令.对于二元函数的连续性问题,结合教材中的定义,以及文献[4]中给出的观察法,文中也给出了典型实例进行了分析,给出了图形和作图的命令.在教学实践中使用Mathematica 作图并进行具体分析,有助于学生很好地理解一些抽象的高等数学问题,进而取得良好的教学效果.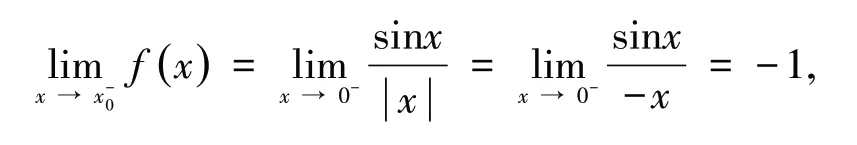


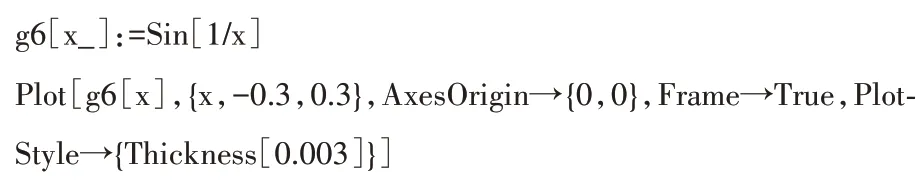

3 二元函数的连续性
4 结语
