数学核心素养视角下的高等代数教学思考
2020-10-16李秀英宋元凤高玉峰张淑娜王耀坤张桂颖
李秀英,宋元凤,高玉峰,张淑娜,王耀坤,张桂颖
高等代数是高等院校数学专业的一门重要基础课程,同时也是考取数学专业硕士研究生的必考科目之一.它对学生的解题运算能力、逻辑推理能力与抽象概括能力的培养起着至关重要的作用.但是,高等代数的特点是概念众多,内容抽象,逻辑性强,许多学生对这门课程的学习存在一定困难.为了达到更好的教学效果,帮助学生克服学习这门课程中的困难,提升学生数学思维能力与应试技巧,我们在高等代数的教学中不断探索,注重知识传授的同时关注数学核心素养的培养.
1 数学核心素养与高等代数课程
教育部重大委托项目“我国基础教育和高等教育阶段学生核心素养总体框架研究”于2013年5月启动.“核心素养”这个概念,是教育部在2014年《关于全面深化课程改革落实立德树人根本任务的意见》中首次提出的[1].核心素养,是指学生应具备的适应个人终身发展和社会发展需要的必备品格和关键能力.数学核心素养是数学课程目标的集中体现,是在数学学习和应用的过程中逐步形成和发展的.数学核心素养是具有数学基本特征的适应个人终身发展和社会发展需要的人的关键能力与思维品质[2].高中数学课程标准指出,高中数学教育的最终培养目标是“三会”,即会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界,这就是高中阶段数学核心素养的体现.而高师院校数学专业学生数学核心素养的培养,最终要落在数学学科核心素养的培养上.所谓学科核心素养,就是指学科的思维品质和关键能力[3].数学学科主要培养的是逻辑思维,而逻辑思维主要包括演绎和归纳.高等代数等课程,是培养学生逻辑思维能力的关键课程.教学中如何创设合适的教学情境,抓住教学的本质,培养学生独立思考的能力,使学生适应当今信息时代的要求,积累思维和实践的经验,形成和发展核心素养具有重要意义.目前有文献关注大学数学或高等数学核心素养的问题[4-5],但对数学核心素养视角下的高等代数的教学研究还不充分.
高等代数主要包括行列式、线性方程组、矩阵、二次型、线性空间、线性变换、欧氏空间等内容.其中行列式和矩阵是高等代数中最基础的内容,同时也是高等代数的重要工具.而行列式起源于解线性方程组.矩阵是高等代数的核心,运用矩阵的初等变换给出了行列式的三角化计算方法(将行列式化为上(或下)三角形行列式);线性方程组可简化为矩阵表达形式,利用矩阵的初等变换给出了线性方程组解法(高斯消元法),通过系数矩阵与增广矩阵的秩关系给出线性方程组有解判别定理;定义二次型的矩阵,二次型可转化为矩阵表达形式,从而二次型的问题与矩阵问题相互转化;在n维线性空间中给定一组基,定义线性变换在该基下的矩阵,从而将线性变换与矩阵对应,使得线性变换的问题与矩阵问题相互转化;n维欧氏空间中正交(对称)变换与正交(对称)矩阵在标准正交基下相对应[6].教学中紧紧抓住矩阵这个核心问题,对学生数学学科核心素养的养成将起到事半功倍的作用.我们认为,高等代数教学应抓住矩阵这个核心,培养学生多项式运算、计算行列式、解线性方程组、矩阵运算的核心计算能力,矩阵理论、线性空间理论、二次型理论、线性变换理论、欧氏空间理论等的逻辑推理与抽象概括能力.这就是数学核心素养在高等代数中的体现.
2 数学核心素养下的高等代数教学实践
2.1 注重代数导论课教学设计
我国著名教育家、化学家傅鹰指出:“一门科学的历史是这门科学中最宝贵的一部分,因为科学只能给我们知识,而历史却能给我们智慧.”因此,代数导论课就从代数发展史说起,使学生了解这门课的历史背景.1859年,我国数学家李善兰首次把“algebra”译成“代数”[7].作为中学数学课程主要内容的初等代数,其中心内容是方程理论.代数方程理论在初等代数中是由一元一次方程向两个方面扩展的:其一是增加未知数的个数,考察由几个未知数的若干个方程所构成的二元或三元方程组(主要是一次方程组);其二是增高未知量的次数,考察一元二次方程.在高等代数中,一次方程组(即线性方程组)发展成为线性代数理论;而二次以上方程发展成为多项式理论.十七世纪日本数学家关孝和提出了行列式(Determinant)的概念,他在1683年写了一部名为《解伏题之法》的著作,意思是“解行列式问题的方法”,书里对行列式的概念和它的展开已经有了清楚的叙述.而在欧洲,第一个提出行列式概念的是德国的数学家,微积分学奠基人之一莱布尼兹(LEIBNITZ,1693年)[8].1750年克拉默(CRAMER)在他的《线性代数分析导言》中发表了求解线性系统方程的重要基本公式(即人们熟悉的克拉默(CRAMER)法则).1764年,BEZOUT 把确定行列式每一项的符号的手续系统化了.对给定了含n个未知量的n个齐次线性方程,BEZOUT证明了系数行列式等于零是这方程组有非零解的条件.VANDERMONDE 是第一个对行列式理论进行系统的阐述(即把行列式理论与线性方程组求解相分离)的学者[9].并且给出了一条法则,用二阶子式和它们的余子式来展开行列式.就对行列式本身进行研究这一点而言,他是这门理论的奠基人.1850年,英格兰的SYLVESTER J J首先提出了矩阵(Matrix)这个词[8],它来源于拉丁语,代表一排数.在1857年矩阵代数得到了ARTHUR CAYLEY 的进一步发展[10].虽然从表面上看,行列式和矩阵不过是一种语言或速记,但大多数生动的概念能为新的思想领域提供钥匙.事实上,这两个概念是数学物理上高度有用的工具.而早在九章算术中就有关于三元一次方程组的实际例子[10],算筹图如图1 所示,为看图方便,改为横排.
上等谷3 束,中等谷2 束,下等谷1 束,共是39 斗;
上等谷2 束,中等谷3 束,下等谷1 束,共是34 斗;
上等谷1 束,中等谷2 束,下等谷3 束,共是26 斗;
求上、中、下三等谷每束各是几斗?

图1 九章算术中的算筹图
九章算术中给出了解法,即后来的高斯消元法.通过上述关于行列式、线性方程组、矩阵等内容的历史背景的介绍,使学生对初等代数与高等代数做到了无缝对接,了解了相关基础内容的浓厚的文化底蕴,陶冶了学生情操,调动了学生学习的积极性.
教育心理学家布鲁纳强调“无论我们选教何种学科,都必须使学生理解该学科的基本结构”.在代数导论中,给出高等代数课程结构图,使学生了解整体知识结构框架,对这门课程知识点有整体的认知.
美国数学家哈莫斯认为数学思想方法是数学的灵魂.导论课教学中,简介高等代数中的思想方法:等价分类思想、同构思想等,通过渗透数学思想方法,使学生感悟这门课程的数学灵魂.这里不再一一赘述.
2.2 采用线上线下混合式教学方式
为方便学生更好地完成自主学习,配合线下教学,我们将课件、教案、练习等内容上传到学习通平台,方便学生完成预习新知与复习已学内容.线下教学中,在学习行列式时,由线性方程组的解引入二阶行列式,引导学生发现规律,由此推广到一般情形,总结给出n阶行列式概念.并通过几何意义增加直观感,如二阶行列式的几何意义是它的绝对值等于平面上以向量为邻边的平行四边形的面积,如图2 所示.
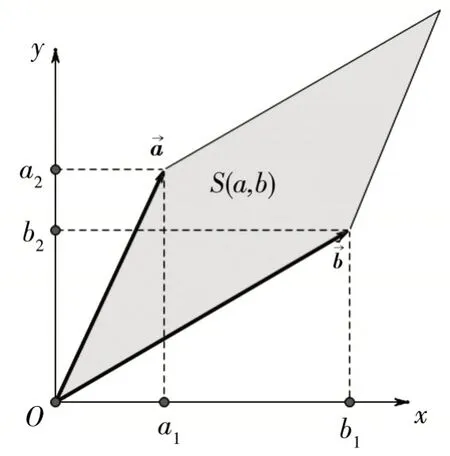
图2 行列式的几何意义
如何灵活运用行列式的基本性质进行行列式的计算是本章的难点.通过例题引导学生根据行列式的特点总结出相应的计算方法:
①各行(列)加减同一行(列)的倍数(适用于加减后某一行(列)诸元素有公因子的情形或为三角形);
②将各行(列)加到同一行(列)上去(适用于各行(列)诸元素之和相等的情形);
③逐行(列)相加减(适用于后行(列)是相邻的前一行(列)的元素的倍数或经这样处理后可看出某些规律);
④递推法(适用于除个别的行(列)外,各行(列)所含元素的形式基本相同)等.
这样的做法培养了学生的抽象思维能力,同时增强了其行列式的计算能力,并提高了其应试能力.
基于数学核心素养的教学,要求教师善于抓住知识的本质,通过创设合适的教学情境[3],启发引导学生自主思考,让学生掌握所学知识与技能的同时,感悟知识的本质,掌握解决问题的技巧方法,形成和发展数学核心素养.
疫情发生以来,采用线上教学,主要运用学习通平台+QQ 直播分享屏幕方式. 每次课提前10 分钟发起直播,配合节奏舒缓、旋律优美的钢琴曲等待学生加入,使学生带着愉悦的心情走入课堂.通过分享抗疫战疫故事,将有哲理的名言警句融入课堂.鼓励学生脚踏实地,勤学苦练,勇于克服困难,迷惘中不失成长,困惑中不失方向.教学设计中,学生通过教学视频完成预习,教师通过直播教学还原课堂教学,增加亲切感,使教学更有温度.直播讲解重点、难点,解决学生的问题.比如在学习正交变换内容时,通过学习通发布主题讨论:欧氏空间中的同构映射与正交变换的关系,使学生更好地把握正交变换的实质;通过发布随堂练习1(见图3):若σ是n维欧氏空间V的正交变换,则以下不正确的是:
A.σ保持向量內积不变;
B.σ保持向量长度不变;
C.σ在任何一组基下的矩阵为正交矩阵;
D.σ是可逆变换.
考查巩固正交变换的等价条件. 发布随堂练习2(见图4):如果两个矩阵均为正交矩阵,那么它们的乘积也是正交矩阵,考查学生正交矩阵性质的掌握情况.这样以问题为驱动使学生参与教学,调动了学生的学习热情.通过学生完成练习的情况,教师可以更好地把握学生的学习情况.
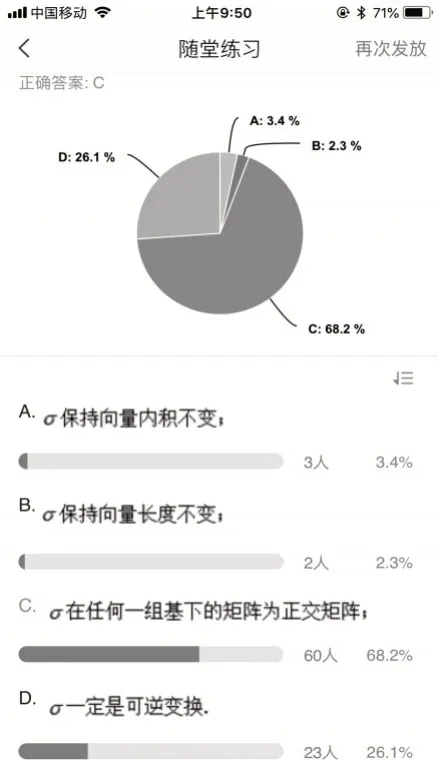
图3 随堂练习1 完成情况

图4 随堂练习2 完成情况
针对一些计算题、证明题等,课上让学生完成后上传QQ 群,及时了解学生的听课效果.同时,完成情况将计入过程性考核中,学生增加了紧张感与挑战度.或将解题过程拍照签到,或上传作业中等.每章末引导学生完成思维导图,上传学习通完成签到.或以发布作业方式,要求学生通过EV 录屏等完成讲解.教师及时总结,分享优秀的作品,相互促进,共同提高.思维导图及教师批阅情况如图5 和图6 所示.
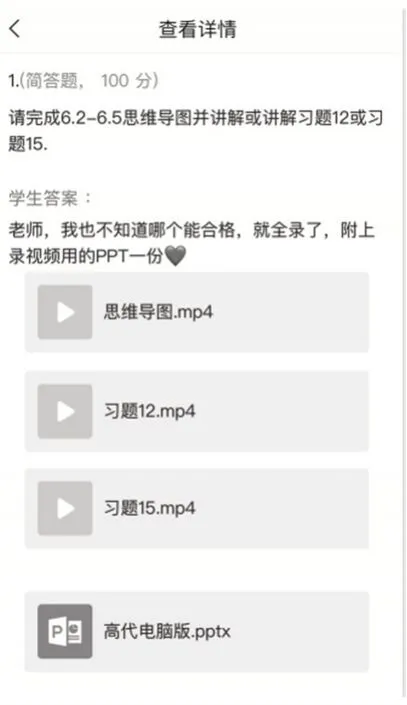
图5 思维导图作业

图6 教师批阅
教学过程中,关注学生对知识的理解,同时关注学生数学思维能力的达成.关注教学内容的融合与分解.针对课程特色,强调知识点之间的整体架构(见图7),力求培养学生的整体知识脉络.这些做法体现了对学生数学学科素养的关注.再如学习实对称矩阵标准形时,学生经常将矩阵合同、相似对角化、正交相似对角化混淆,为此通过结构图(见图8)讲解,便于学生理解掌握.
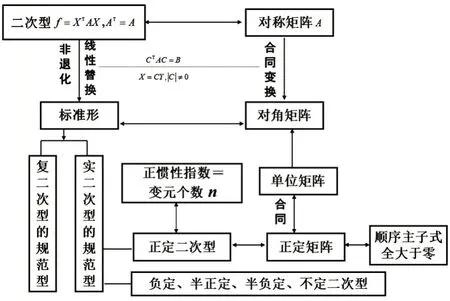
图7 二次型结构图
3 结论
总之,高等代数教学中我们要全面关注数学核心素养的培养.把握高等代数课程整体结构框架—主线—主题—关键概念、定理、思想方法等,精心设计并实施教学.将高等代数教学过程与核心素养有机融合,推动基于核心素养的教学改革.

图8 矩阵合同(或相似)于对角矩阵结构图
