浅议银氰配合物稳定常数

王 晖，王毓明

1 配合物的稳定性及其稳定常数的测定方法

热力学是配位化学的重要组成部分，配合物的稳定性是热力学研究内容之一.配合物的稳定性是指在平衡状态下，由组分生成配合物的程度，其大小可由稳定常数判断.

配合物的稳定性在化学上有它特殊的意义，主要用于判断配合物是否稳定.配合物的稳定性包括配合物的热稳定性、氧化还原稳定性、在水溶液中的稳定性、在非水溶剂中的稳定性、在融盐中的稳定性，以及在气态时的稳定性，通常是指配合物在水溶液中的稳定性.配合物在水溶液中的稳定性除指是否离解或分步离解为它的组成部分外，还包括配合物在溶液中是否进行酸离解或碱离解（即是否进行质子传递反应）、中心离子氧化态是否稳定（是否易被氧化或还原）［1］.

配合物在水溶液中的稳定性用稳定常数表示（配合物在溶液中进行离解的强度）.配合物的稳定常数可通过实验方法测定，传统测定方法有：①pH 测定方法或电位滴定法；②电位测定法（电动势法）；③极谱测定法；④光度测定法；⑤离子交换法；⑥溶解度法；⑦溶剂萃取法；⑧动力学测定常数法（借反应速度来测定）；⑨电导法；⑩冰点下降法和热量法.在这些配合物稳定常数测定方法中，较经典的方法是电位测定法和分光光度法，也是较可靠的方法［1］.现代测定方法有：①核磁共振法；②顺磁共振法；③折射法；④测温滴定量热法.配合物热力学稳定常数的测定已研究了半个多世纪，提出的测定方法有20 多种，其中较常用的是pH 滴定法和分光光度法［2］.

2 疑惑试探析

配合物的稳定常数除少数是理论计算得出外，大多数通过实验测得.精确测定稳定常数是一项艰巨的研究工作，同一配离子的稳定常数值用不同方法测定会有差异.故有些化学手册或专著中列出稳定常数值时，除注明温度、离子强度外还注明测定方法以及原始文献，以供读者使用时参考［3］，然而笔者发现，目前大学教科书没完全做到这一点，致使笔者在解答配位平衡反应时出现两种矛盾的答案.

2.1 在沉淀溶解平衡计算中遇到的问题

在讨论配位平衡与沉淀溶解平衡的关系时，沉淀生成和溶解以及配合物的解离和形成的反应方向可由反应平衡常数K值进行判断［4-5］.如：

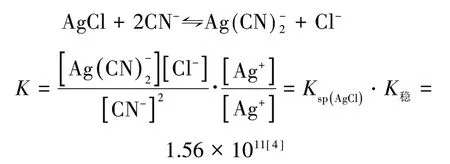
还可从标准电极电势角度进行计算：

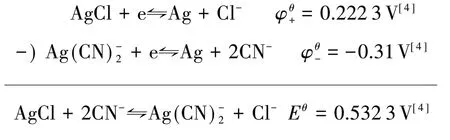
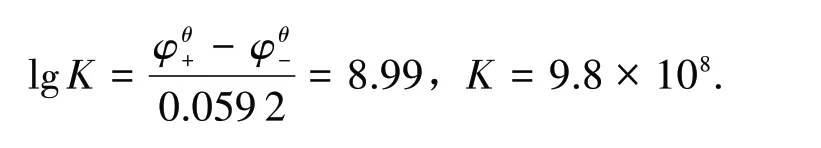
两种方法所得结果不相符，差别较大.同样在AgBr、AgI 溶解平衡计算中也发现差别较大，见表1.

表1 不同方法计算配位溶解反应平衡常数值对照表

2.2 在配位反应平衡计算中遇到的问题

在其他配位反应平衡中，如：

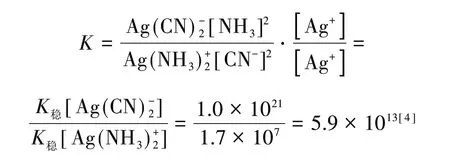
通过电极电势计算得：

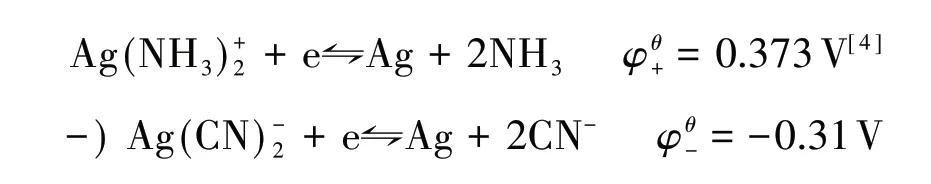
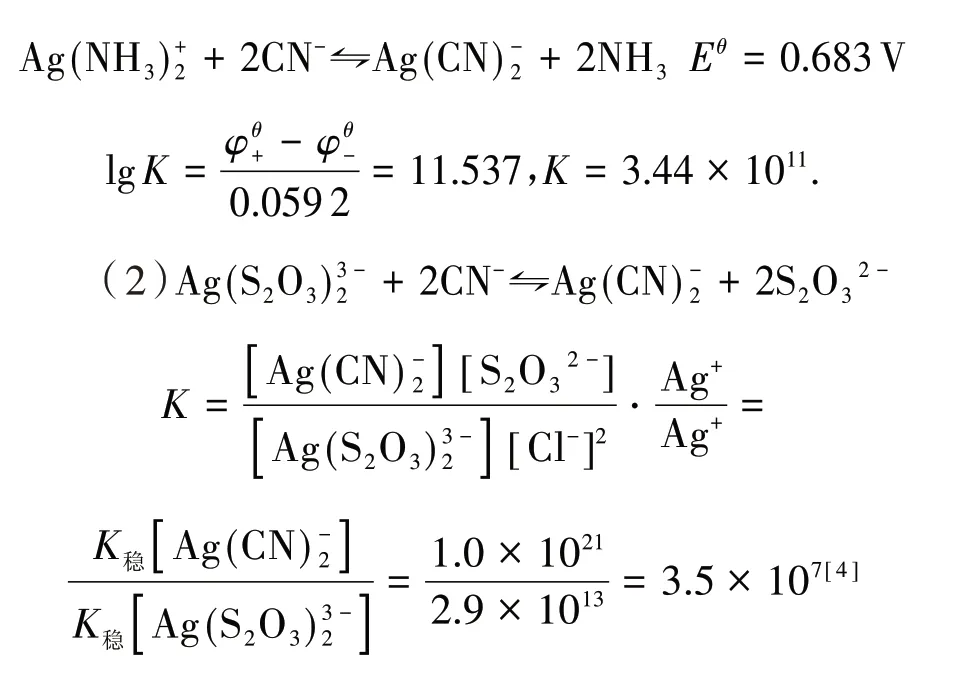
通过电极电势计算得：

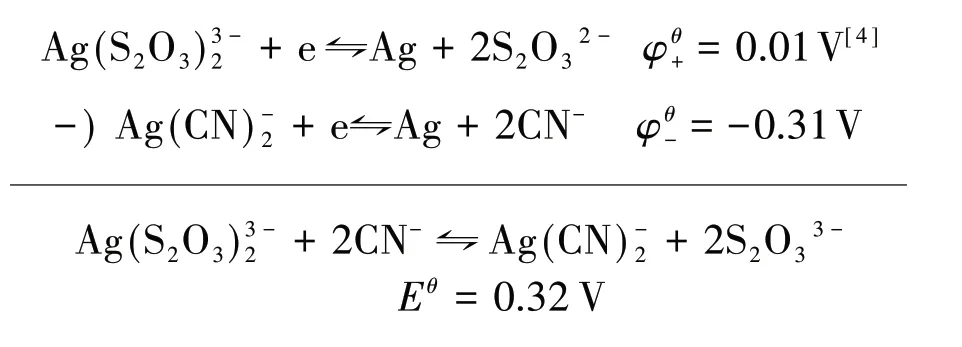
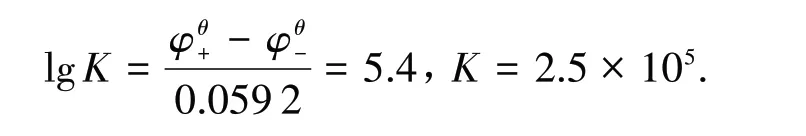
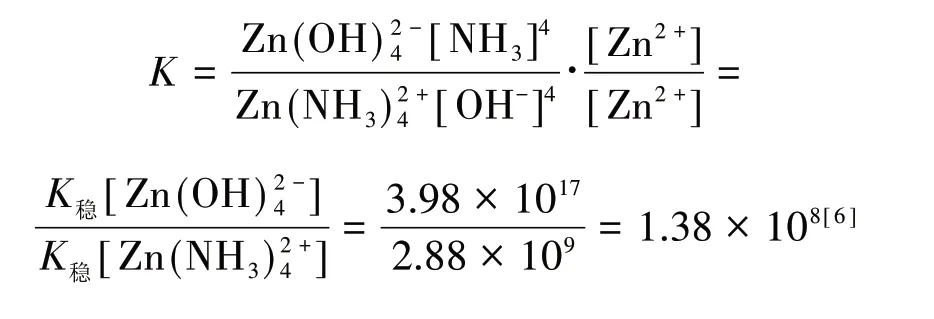
通过电极电势计算得：

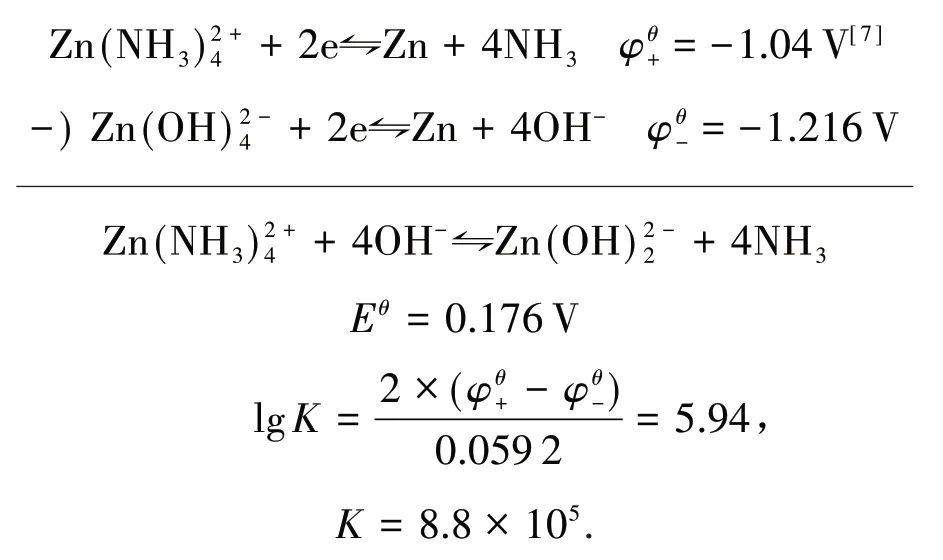
为了便于观察，上文用不同方法计算的反应平衡常数值列于表2.

2.3 探析所遇问题

为什么用不同方法计算反应平衡常数所得的数值不一致，因为我们尚不知道Ksp和K稳是通过何种方法测定，不可妄加评说.笔者现以电势法计算Ksp和K稳，先求Ksp：

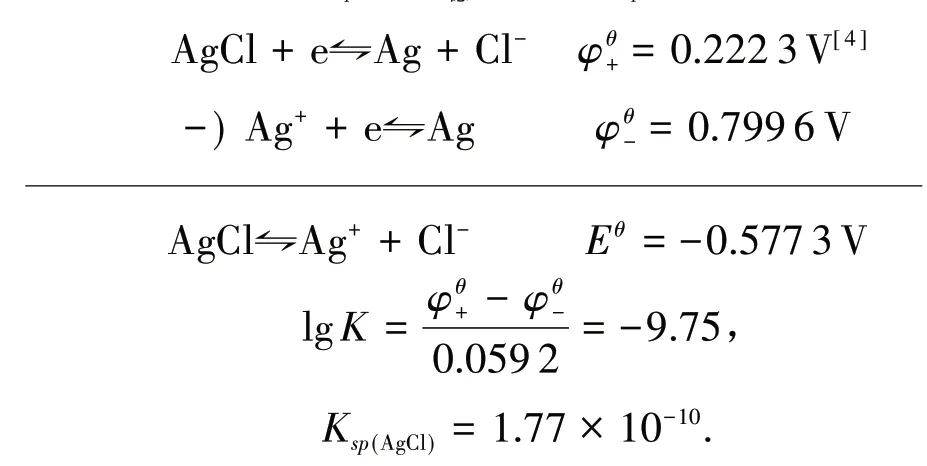
同理可求得

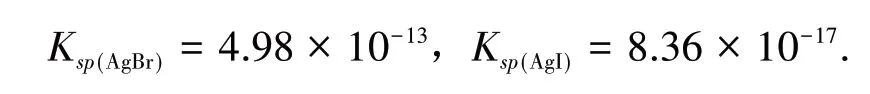
再求K稳值：

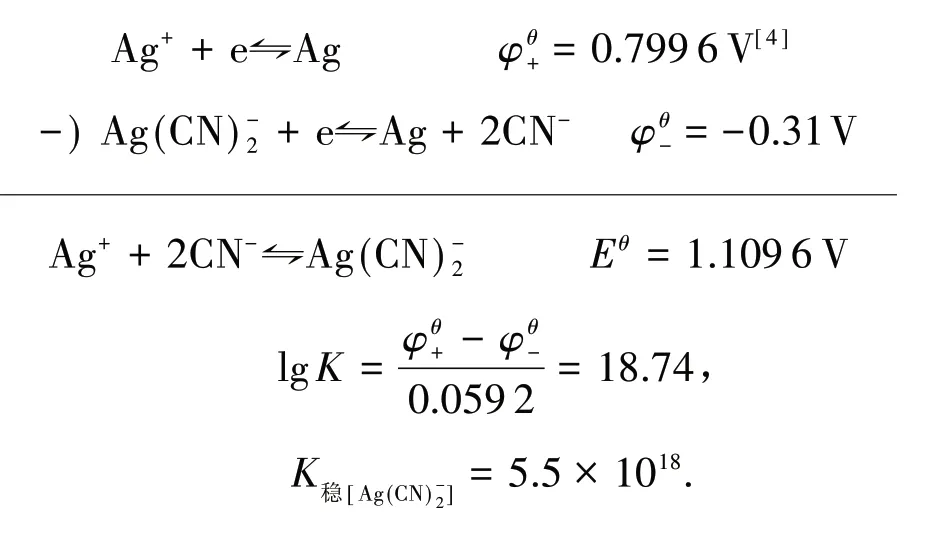
同 理 可 求 得K稳［Ag（NH3）+2］=1.6×107，K稳

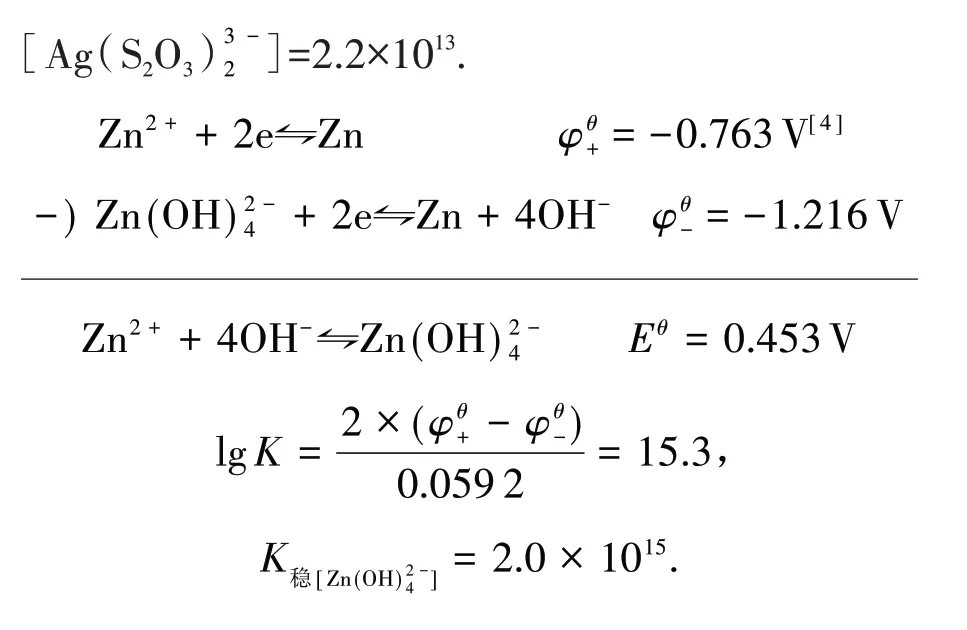
将上面计算所得数值列于表3.从表3 可知，虽然计算配位反应平衡常数的方法不同，但所得结果应是一致的，如果不一致会使初学者无所适从，疑惑不解.

3 所遇问题探究及建议

3.1 不同版本教科书引用的数据有差异

回到开头所遇到的问题，同一配离子用不同的方法测得的稳定常数有差异，因此在教科书中列出稳定常数值时应注明测定方法及出处，详见表4.

表2 用不同方法计算配位反应平衡常数值对照表

从表4 所列数值看出，王致勇等［7］编写的《简明无机化学教程》附录中采用的溶度积常数、配离子稳定常数与本文以电势法求得数值基本一致.有些教材K稳数据来源没有注明出处［4-5］，标准电极电势表引自《Lange’s Handbook of Chemistry》，有的采用11th ED（1973）［6］，有的采用12th ED（1979）［4］，也有的采用13th ED（1985）［7］，也有引自《Handbook of Chemistry and Physics》69th ED（1988）［4］，至于哪个准确可信可用，对于教材，笔者认为应予统一.

表3 电势法测定不同平衡反应的反应平衡常数

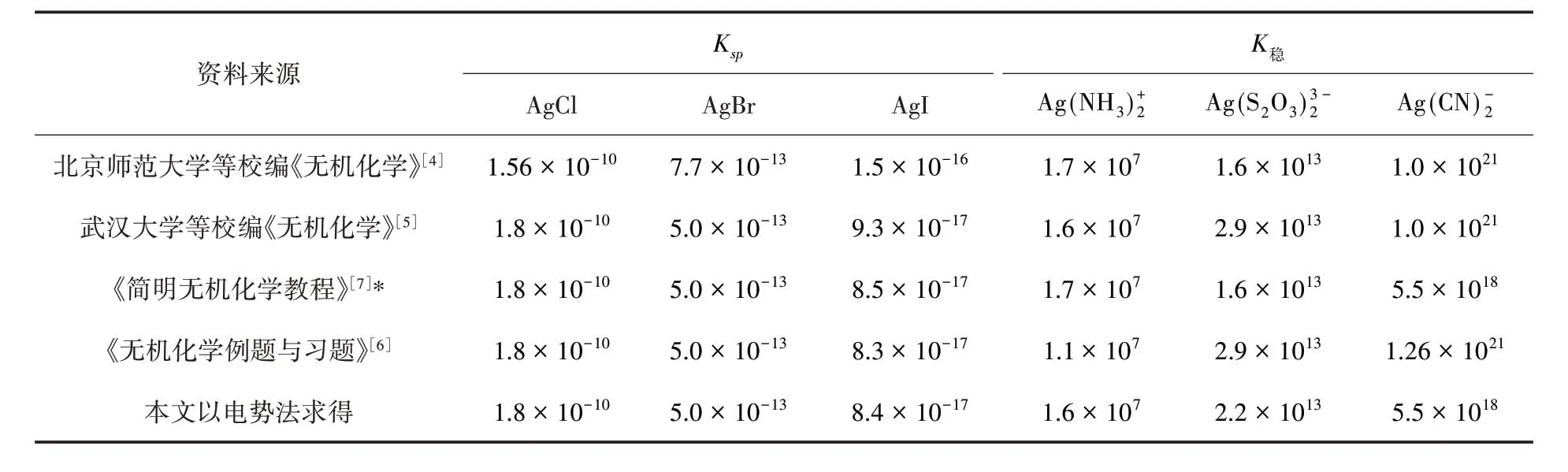
表4 不同版本教材部分Ksp 和K稳值对照表

3.2 兰氏化学手册和国外教材K 稳值对比

兰氏化学手册和国外教材所用的K稳值有差异，特别是氰配离子的K稳值差别较大，见表5.

表5 兰氏化学手册与Latimer、Petrucci 书中部分配离子K稳值对照表

3.3 从电势法角度比较

从电势法角度进行比较也发现，金属氰配离子/金属电对的标准电极电势值在兰氏化学手册与Latimer 书中附录中也有不同，见表6.

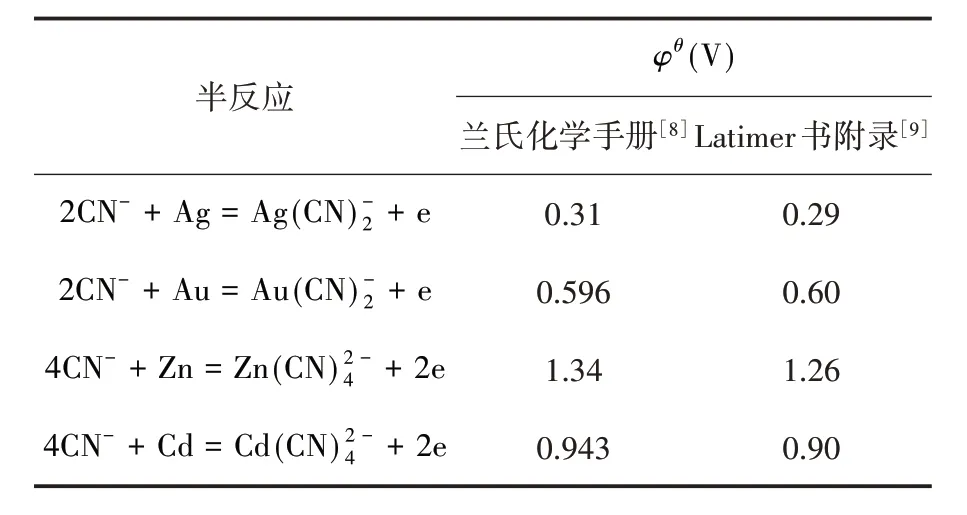
表6 兰氏化学手册与Latimer 书中部分半反应φθ 值对照表

从表6 提供的数据可看出，不同教材引用来源不同，氰配离子的K稳值数值不同，作为教材，应予统一规范，必要时需要重新测定.

为说明Eθ值不同造成的后果，我们依2.3节方法，查出半反应的φθ，通过lgK=nEθ/0.05916公式求得K稳，如：

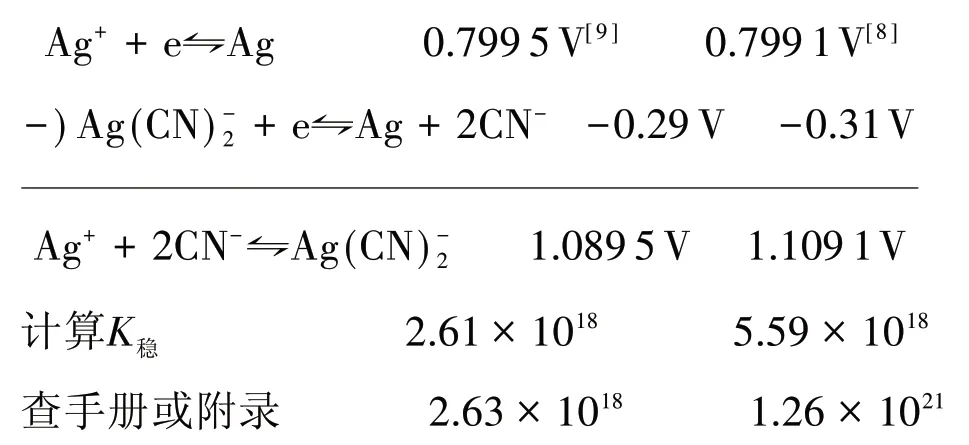
从上面计算结果看出，兰氏化学手册上的K稳与通过Eθ和K关系式计算出的K稳数值相差较大.

3.4 从热力学角度比较

从热力学角度进行比较，可通过配位反应的标准自由能改变量ΔrGθ与反应平衡常数的关系lgK= -ΔrGθ/5.706，求得K稳，如：

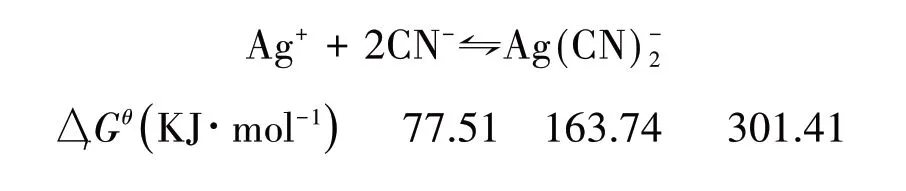
Latimer［9］求得K稳= 1.23 × 1018，兰氏化学手册［8］求得K稳= 2.63× 1020.

我们将此K稳与3.3 节所得数值列于表7，便于对照.由表7 可知，兰氏化学手册自身体系提供的数据，与相关的数据关联性欠佳，用不同方法计算出的K稳值殊途不同归；而Latimer 自身数据关联性颇佳，通过不同方法计算出的K稳值基本一致，应是可靠、可信的.国外普通化学教材［10］附录中的K稳标示为5.6×1018，故本文开头所遇到的问题出在的K稳值差错上，建议目前的无机、普通化学教材中采用的K稳=1.3×1021应予纠错，并统一规范附录中采用的数据.

4 结语

表7 不同出处的数据以不同途径求得Ag(CN)的K稳 对照表

表7 不同出处的数据以不同途径求得Ag(CN)的K稳 对照表

数据来源Latimer［9］兰氏化学手册［8］K稳2.63× 1018 1.26 × 1021从Eθ求得K稳2.61× 1018 5.59 × 1018从ΔrGθ求得K稳1.23× 1018 2.63× 1020

随着科学技术的发展，配位化学的热力学研究主要集中于常规研究方面，金属离子与普通配体生成的配合物热力学研究不再是研究的重点，能引起兴趣的是金属离子与一些新合成的配体生成的配合物或新配合物的热力学研究［11-16］.故本文提出的问题涉及经典的、沿用半个世纪的成熟数据，恐难引起关注，本着实事求是的科学精神，大胆提出，供同行专家、学者研判.

教科书偏重于介绍稳定常数的应用，较少或缺乏介绍稳定常数的测定方法，数值的提供亦多未注明出处，不同教材提供的数值有差异，甚至在稳定常数值表上所标明数值与课文中举例说明所用数值不一致.作为教材，必须统一规范，这是笔者所期望的，不当之处敬请专家读者指正.