发动机材料高周疲劳P-S-N曲线优化处理方法

2020-10-16李旭东赵延广陶春虎

航空材料学报 2020年5期

许巍,陈新,李旭东,钟斌,赵延广,陶春虎

（1．中国航发北京航空材料研究院，航空材料检测与评价北京市重点实验室，中国航空发动机集团材料检测与评价重点实验室，北京 100095；2．大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116085）

对于航空发动机而言，材料疲劳性能是影响服役安全性和可靠性的主要性能之一。而发动机材料的高周疲劳性能参数不但是性能评价的关键依据，更是发动机强度设计和寿命预测的必要参数[1]。因此针对发动机材料开展高周疲劳性能数据的测试和表征至关重要。随着概率设计和可靠性设计理念在发动机强度设计中的广泛采用，各型号发动机的设计过程中均提出了针对关键材料高周疲劳P-S-N曲线的处理要求，有时甚至要求给出含多个P值（存活率或可靠度）和置信度的高周疲劳曲线。

截止目前，国内外学者针对高周疲劳P-S-N曲线提出了许多数据处理的方法，这些方法各有特点。其中广泛使用的方法是极大似然法[2-3]和最小二乘法[4]，这些方法在处理高置信度P-S-N曲线时对数据样本量的要求较高。由于航空发动机材料成本往往较高，且高周疲劳测试项目普遍较多，因此试样数量往往存在一定限制，所以满足发动机材料高周疲劳P-S-N曲线处理更倾向于使用基于小子样的方法。近年来发展了一些基于小子样的方法[5-8]以及人工神经网络方法[9]和贝叶斯方法[10-11]，均可实现P-S-N曲线的处理和高周疲劳寿命的可靠性评估，这些方法对实验数据量的要求有所降低，但大多针对高周疲劳测试中成组法获得的数据进行处理，对升降法获取数据（即长寿命区）的处理缺乏针对性，而实际航空发动机强度设计中对长寿命区的数据需求更为迫切，应同时考虑成组法和升级法获取数据以得到完整的P-S-N曲线。因此，上述处理方法大多无法全面满足发动机材料高周疲劳性能数据要求。

相比而言，国家军用标准《金属材料力学性能数据处理与表达》（GJB/Z 18A-2005）所给出的高周疲劳P-S-N曲线处理方法基本能满足上述要求，不过仍然存在一些不足。首先，该标准所述方法针对长寿命区的实验数据处理只给出指导原则，缺乏具体的处理步骤和方法；其次，该标准方法仅仅针对寿命范围为107循环数以内的疲劳曲线处理，针对更高寿命范围（例如 3 × 107以上）的数据，该标准并没有给出相应的处理方法，对于最高循环数达到108及以上的超高周疲劳性能数据，该标准所述方法更无法适用；最后，由于发动机材料疲劳性能具有数据规模大、种类多的特点，同时可能还需要考虑不同加载方式、应力比和温度的影响，因此发动机型号相关的高周疲劳性能数据通常处理工作量非常大，提高处理效率十分迫切，然而目前缺乏高周疲劳数据批处理等优化方法，无法满足发动机材料领域大量疲劳数据处理的实际需求。

本工作针对高周疲劳P-S-N曲线处理过程中的关键环节提出改进方法，以确定数据处理过程中的关键参数，对处理流程进行优化，然后通过编制MATLAB程序实现P-S-N曲线的优化处理，给出在某型航空发动机用钛合金材料高周疲劳和超高周疲劳P-S-N曲线处理的应用算例，并对比了本方法与传统方法的处理效率。

1 基本思想

目前，三参数幂函数模型在高周疲劳中值S-N曲线和P-S-N曲线的处理中应用较为普遍，三参数幂函数模型的表达式见式（1）：

式中：Smax和Nf分别表示最大应力和失效循环数；B1、B2和B3表示拟合参数，均为正数，通常采用最小二乘法确定。需要指出是，有时根据数据分布特点，三参数模型可能无法拟合出相应的高周疲劳曲线，于是可以采用式（2）所示的二参数模型来实现拟合：

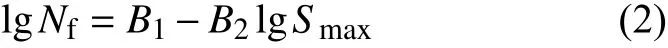
对于P-S-N曲线，可采用三步法来对数据处理。第一步；针对高周疲劳实验数据的高应力、中等寿命区进行处理，计算这个区域数据的中值曲线和标准差。这里假设疲劳性能参数服从对数正态分布，于是可通过中值偏移公式（3）和单侧容限系数公式（4）得到高应力、中等寿命区性能处理数据。

第二步：在得到高应力、中等寿命区的处理后数据后，再针对长寿命区的性能数据进行处理，将长寿命区统计性能的数据点用修正的威尔逊方法求出。第三步：将前两步得到的全部数据点用三参数幂函数法进行拟合，即可得到高周疲劳P-S-N曲线方程。关于修正的威尔逊方法，在文献[12]中已有详细介绍，这里不再赘述；但是有一点需要强调，威尔逊方法仅在最大循环数107处生成一系列数据点，并根据式（3）和式（4）计算得到一定存活率和置信度的数据点。然而，仅有最大循环数一处的数据点，难以达到理想的P-S-N数据处理效果，因此需在长寿命区的不同指定循环数条件下（例如5 × 105、106、5 × 106等）运用修正的威尔逊方法获得不同的偏移点，这样就可以利用这些点绘制出较为理想的P-S-N曲线。

2 数据处理流程

2.1 拟合模型的选择

前面已经指出，对于高周疲劳曲线（中值S-N和P-S-N）可以根据数据情况分别采用方程(1)和方程(2)所述的三参数和二参数模型来实现拟合。如何选择模型类型在实际数据处理中至关重要，传统观念认为用拟合过程中的相关系数r来判断哪种模型更为合适[13]，应该选择r相对较大的模型来拟合高周疲劳实验数据，虽然这种说法本身没有问题，但是仅仅依据r大小来判断，可能无法对采用何种模型做出准确判断。下面给出本工作提出的拟合模型的选择方法。

根据式（1），易导出公式（5）：

对式（5）两边取极限，可以得到：

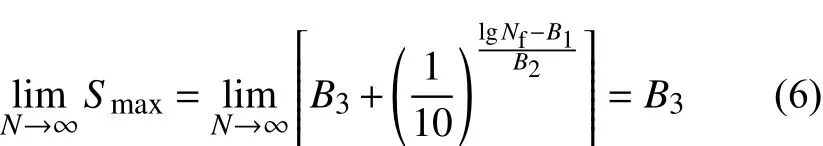
由式（6）可以判断，当循环数N趋近于无穷大时，最大加载应力Smax趋近于B3，从数学意义上说，B3可以认为是高周疲劳曲线的疲劳极限，于是B3需满足 B3> 0 的要求，另外，由式（1）结合对数的基本性质可知 Smax–B3> 0，于是可得：

事实上，当利用最小二乘法处理实验数据时，最后通过求解一个关于B3的非线性方程f（B3）=0来得到B3，该非线性方程的形式较为复杂，这里不详细给出，具体求解可采用数值计算方法（例如二分法）来实现，该非线性方程形式及求解过程可参见文献[13]。利用二分法求解的前提是B3所在的求解区间端部存在正负相反的函数值，此求解区间即是式（7）所示区间，于是，f（B3）= 0 存在非零解的前提是：

式中，ξ表示一个小量，可设置为0.001，设置该小量的原因是B3的求解区间为半开区间，如式（7）所示，B3不能等于Smax。如果式（8）不满足，则在该求解区间内 f（B3）= 0 无解，即式（1）所述的三参数模型无法实现对该组疲劳实验结果的拟合，于是采用按式（2）所述的二参数模型进行拟合。所以在拟合模型的选择上，完全可以实现自动判断，通过程序一次性完成数据处理。

2.2 临界点的优化确定

目前，对于中等寿命区和长寿命区的临界点缺乏明确的判断依据，即使是国军标GJB/Z 18A—2005，对于高应力（中等寿命）区和低应力（长寿命）区的临界点，也没有给出明确的判断方法，标准原文的表述是：“中等寿命区与长寿命区之间的分界，可直接或从双对数坐标上通过观察实验点在S-N曲线图上的分布状况凭经验确定，一般可取3 × 105周~5 × 105周处的应力作为界线”。实际数据处理过程中如果凭经验确定临界点，必然会造成数据处理结果因人而异的不利局面。

另一方面，随着发动机材料对循环周次数要求的提高，高周疲劳实验的目标循环数已经不局限于传统的107周次[14-15]，而在更高目标循环数的高周疲劳测试中，其临界点对应的循环周次也不局限于“3 × 105周~5 × 105周处”范围内。考虑到高周疲劳曲线的测定过程中针对中等寿命区和长寿命区分别采用成组法和升降法，可以认为中等寿命区和长寿命的应力临界点实质上就是成组法和升降法的应力临界点。

将达到目标循环数而试样不发生破坏的点定义为溢出点（run out，RO），在升降区所包含的所有的溢出点中，最大的应力级通常作为升降区的起点，而由于升降法中数据配对和闭合的要求，该起点的上一级破坏点通常也被纳入升降区范围。因此，先将所有溢出点中的最高应力级的更高一级应力作为临界应力，即临界应力Scritical可以用式（9）表示：

2.3 数据的批处理方法

实现高周疲劳性能数据高效处理的关键是数据的批处理，批处理的基本途径是实现原始数据的批量导入、自动化处理和批量输出。本工作提出的批处理方法具体流程如下所述：

（1）将多条高周疲劳原始实验数据（应力、寿命）和置信度（γ）、存活率（p）等处理要求依次导入同一个Excel文件；

（2）打开MATLAB软件，并将该Excel文件一次性读入到MATLAB程序中；

（3）通过编制的MATLAB主函数调用P-S-N曲线处理子函数，依次对导入的Excel文件中数据进行逐条处理；

（4）通过式（9）确定临界应力，进而分别将原始实验数据进行分类，分别划入高应力（中寿命）区和低应力（长寿命）区两个区域；

（5）对两个区域内的实验数据点分别进行处理，获得上述两个区域的指定存活率和置信度的偏移数据点，即P-S-N数据点；

（6）将步骤（5）产生的数据点通过三参数或两参数模型进行拟合，通过式（8）来判断采用何种拟合模型，得到拟合参数；

（7）回到步骤（3），重复后续步骤，直到导入的所有数据都处理完毕；

（8）将数据处理得到的所有结果文件一次性导出，批量绘制P-S-N曲线。

上述的高周疲劳数据P-S-N曲线的批处理过程可以用图1所示的流程图来表示。类似地，可以利用此方法实现高周疲劳数据的中值S-N曲线的批处理。

3 高周疲劳实验及数据处理

3.1 高周疲劳实验

针对航空发动机使用的钛合金材料，开展最高循环数为3 × 107周次的200 ℃高温旋转弯曲疲劳实验，材料牌号为TC17，参考的实验标准是航空工业标准《金属高温旋转弯曲疲劳试验方法》（HB5153—1996），试样形状和尺寸见图 2（a）；另外，开展最高循环数为108周次的室温轴向高周疲劳实验，应力比为–1，材料牌号为TA11，参考的实验标准是航空工业标准《金属材料轴向加载疲劳试验方法》（HB5287—1996），试样形状和尺寸见图2（b）。这里需要指出的是，这里所选的两种高周疲劳实验的最高循环数都大于常见的107周次，其中TA11钛合金轴向高周疲劳的最高循环数达到108周次，即可以认为属于超高周疲劳问题所考虑的周次范围[15-16]。

图1 高周疲劳性能数据的批处理流程图Fig.1 Flow chart of batch processing of high cycle fatigue data.

3.2 数据处理结果

采用第2节所述的高周疲劳性能数据处理流程方法，分别对TC17高温旋转弯曲疲劳和TA11轴向疲劳的实验结果进行处理，为了全面满足不同设计需求，需要得到5种情况的曲线，分别是中值S-N曲线和4条P-S-N曲线，其中P-S-N曲线分别考虑置信度为50%的–2σ、–3σ情况和置信度为95% 的–2σ、–3σ 情况。

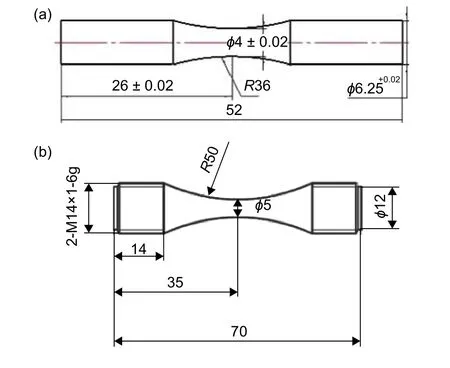
图2 高周疲劳试样的形状和尺寸图（a）旋转弯曲疲劳试样；（b）轴向高周疲劳试样Fig.2 Size and shape of fatigue specimen for comparison（a）rotating-bending specimen；（b）axial-loading specimen.

将原始实验数据和上述5种处理条件通过自编程序一次性导入MATLAB软件中进行计算，通过自编的批处理程序完成P-S-N数据处理，程序自动生成所有情况的拟合曲线和拟合方程的参数。其中，TC17高温旋转弯曲疲劳性能的各条P-S-N曲线见图3（a），可以看出，图中各P-S-N曲线呈现出近似直线的特征，从各曲线分布的特点来看，相同循环数对应的各P-S-N曲线的应力值从大到小排布顺序依次是：中值、置信度为50%的–2σ、置信度为95%的–2σ、置信度为50%的–3σ和置信度为95%的–3σ曲线，其中置信度为95%的–2σ和置信度为50%的–3σ的曲线十分接近。

TA11钛合金轴向高周疲劳的P-S-N曲线见图3（b），图中各条P-S-N曲线表现出明显的弯曲弧度特征，最大应力值随着循环数的增加呈现先快速下降后逐渐趋缓的特点，相同循环数对应的各P-SN曲线的应力值从大到小排布顺序依次是：中值、置信度为50%的–2σ、置信度为50%的–3σ、置信度为95%的–2σ以及置信度为95%的–3σ曲线，尽管其大小顺序与TC17对应各曲线的顺序略有不同，但置信度为95%的–2σ和置信度为50%的–3σ的曲线的同样十分接近。事实上，目前航空发动机设计准则（GJB 241A—2010）中明确提出发动机材料疲劳性能应都用置信度为50%的–3σ值或置信度为95%的–2σ表示。根据图3给出的结果，可以认为这两种置信度-存活率要求下的高周疲劳P-S-N曲线是近似等价的。

图3 高周疲劳的 P-S-N 曲线的处理结果（a）TC17 钛合金 200 ℃ 光滑试样（Kt = 1）旋转弯曲疲劳曲线；（b）TA11 钛合金光滑试样（Kt = 1）室温轴向疲劳曲线Fig.3 Processing results of high cycle fatigue P-S-N curves （a）200 ℃ axial-loading fatigue curves of TC17 Ti-alloy specimens；（b）RT rotating-bending fatigue curves of TA11 Ti-alloy specimens

选用式（1）对应的三参数幂函数模型作为各PS-N曲线的拟合模型，可以通过上述数据处理程序一次性得到各条P-S-N曲线的拟合参数。TC17合金旋弯疲劳和TA11合金轴向疲劳实验结果的拟合参数结果分别见表1和表2。其中，γ和p分别表示置信度和存活率，B1~B3为拟合参数，r为拟合方程的相关系数，用来评价拟合的效果，该值越接近1表示拟合得越好。需要指出的是，由于本程序可以一次性生成拟合参数表，而无需后期人工输入，从而减轻了工作强度，降低了人为操作失误的发生率。

为了定量评估本工作提出方法处理效率，分别采用本程序方法和传统方法对上述TC17和TA11的高周疲劳数据进行处理，处理平台为相同的台式计算机，处理的目标即得到图3所示曲线，并记录处理时间。针对两种材料性能数据的处理时间对比见图4。可以看到，本方法节约了人工判定和操作的时间，数据处理完全由计算机自动处理，所需时间远低于传统方法，本方法的处理效率大约是传统方法的8~9倍。

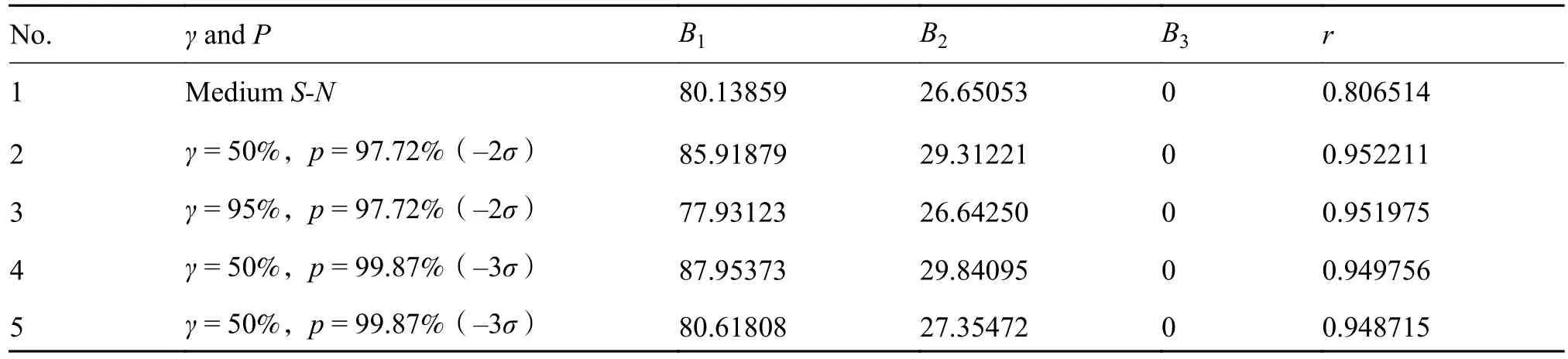
表1 TC17合金旋转弯曲疲劳的P-S-N曲线的拟合参数结果Table 1 Fitting parameter results of P-S-N curves of rotating-bending fatigue testing of TC17 specimens

表2 TA11合金轴向高周疲劳的P-S-N曲线的拟合参数结果Table 2 Fitting parameter results of P-S-N curves of axial-loading fatigue testing of TA11 specimens

图4 实验数据处理时间的对比Fig.4 Comparison of process time of testing data

4 讨论

对于高周疲劳P-S-N曲线而言，其结果受到有效数据点个数的显著影响。在以往的处理方法中，得到高置信度（例如95%）的P-S-N曲线需要的样本点较多，有时一条完整的P-S-N曲线可能需要近百根试样的数据。而采用GJB/Z 18A-2005推荐的方法，对样本点数量的要求显著降低，获取一条完整的P-S-N曲线可能仅需要30多根试样。这主要是因为采用了将实验数据点划分为高应力（中等寿命）区和低应力（长寿命）区的两个区域，在使用单侧容限系数，即式（4）进行偏移值计算时，其数据点个数是以每个区域的数据点总数为基础的，而两个区域的数据点个数大致相等，所以数据点数量保证了得到的单侧容限系数和P-S-N曲线的合理性。尽管如此，在实际的高周疲劳实验过程中，特别是对于某些疲劳性能分散性较大的材料，还是希望能尽量多地获得有效实验数据点，以获取更具有实用价值的P-S-N曲线。

此外，还有一点需要指出，本工作所提出的优化的高周疲劳P-S-N处理方法并非对所有的高周疲劳实验数据都适用。符合现行实验疲劳标准的高周疲劳实验一般针对高应力（中等寿命）区和低应力（长寿命）区，会分别按照成组法和升降法来确定实际加载应力，对于这种情况下的实验数据，按照前面2.2节提出的临界应力判断方法可以有效确定临界应力。如果并没有按照成组法和升降法安排实验，或者得到的实验数据点分布不规则，可能会导致某个分区的数据点过少或者无溢出点的情况，则本工作提出的临界应力判断方法将无法适用，以至于后续的批处理过程无法顺利进行，在这种情况下，则需要人为确定临界点，以便顺利实现P-S-N曲线的处理。