十字轴式万向联轴器强度与模态分析
2020-10-14杨佩东
杨佩东
(山西工程职业学院,山西030009)
万向联轴器是用来联接不同机构的主动轴和从动轴,使两轴不在同一轴线或存在轴线夹角的情况下,仍能实现传递扭矩和动力。万向联轴器有多种结构型式,包括:球笼式、球叉式、三叉杆式、十字轴式等,其中十字轴式万向联轴器由于具有传递扭矩大、传动效率高、角向补偿能力大以及传动平稳等特点,在轧钢机械方面得到了广泛的应用。但十字轴式万向联轴器在实际工程使用过程中,经常会出现十字轴折断、叉架变形等现象[1],所以对十字轴式万向联轴器进行强度分析与模态分析,具有重要的意义。通过此次研究分析,为十字轴式万向联轴器优化设计以及企业工程实际操作提供一定的思路与借鉴。
1 建立有限元模型
在对十字轴式万向联轴器进行强度分析与模态分析时,首先要建立其三维实体模型。目前较为常用的三维建模软件包括:SolidWorks、UG、CATIA、Pro/E等等,其中SolidWorks因具备强大的功能、操作方便、简单易学等特征,使SolidWorks三维绘图软件在机械工程中得到广泛应用。依据某工厂所使用的十字轴式万向联轴器,采用SolidWorks三维绘图软件进行实体建模,为了减少建模时间以及提高有限元计算效率,在对十字轴式万向联轴器进行建模过程中,作了一定的简化处理。SolidWorks三维实体模型见图1。

图1 SolidWorks三维实体模型Figure 1 3D solid model by SolidWork
2 材料属性与网格划分
在ANSYS Workbench中使用Engineering Data进行设置材料属性,十字轴材料为42CrMo,叉头材料为35MnMo,中间轴为45钢,十字轴式万向联轴器各零部件材料属性见表1。
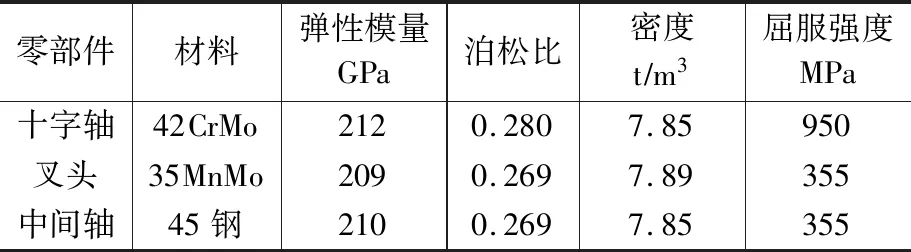
表1 十字轴式万向联轴器各零部件材料属性Table 1 Material properties of cross shaft universal coupling components
使用Mesh模块进行网格划分,网格划分时可以产生的网格单元类型有:四面体单元、金字塔单元和六面体单元等。研究中,采用程序自动控制网格划分方法,其中“跨度角中心”和“网格平滑度”均设置为“中等”,网格化的三维模型见图2。

图2 网格化的三维模型图Figure 2 Grid 3D model
3 强度分析
3.1 静力学理论基础

图4 最大轴向应力云图Figure 4 Cloud chart of maximum axial stress

图5 最大径向应力云图Figure 5 Cloud chart of maximum radial stress
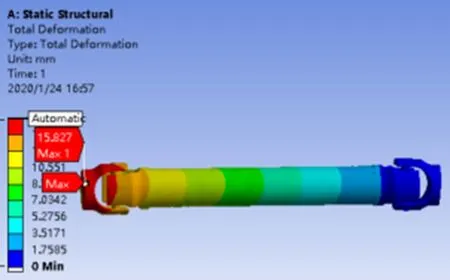
图6 最大位移云图Figure 6 Cloud chart of maximum displacement
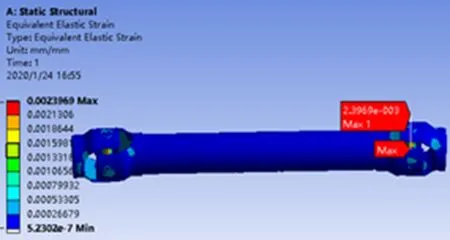
图7 最大应变云图Figure 7 Cloud chart of maximum strain
在ANSYS Workbench中采用静力学分析模块进行强度分析,在经典力学当中,物体的动力学通用公式为:
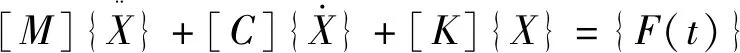
(1)

在静力学强度分析中,如不考虑随时间变化的载荷,则公式(1)简化为[2]:
[K]{X}={F}
(2)
3.2 强度分析
为了真实模拟十字轴式万向联轴器各个零部件的受力状况,对整个装配体进行有限元分析,这样在装配体环境下计算出来的各个零部件受力情况,比单个零件进行受力分析更加精确。为了模拟万向联轴器自身所受重力的影响,对模型整体施加重力加速度,大小为9.8066 m/s2,方向竖直向下。对电机输出端叉头施加扭矩,扭矩大小设置为8 kN·m,方向与电机转动方向相同。在万向联轴器输出端的叉头表面施加位移约束,其中X、Y、Z三个方向的位移约束均设置为0[3]。十字轴与叉头的接触类型设置为摩擦约束,摩擦系数为0.2,用于模拟十字轴与叉头间配合的滚针轴承。在计算求解时,将大变形打开,通过计算得出万向联轴器最大等效应力云图、最大轴向应力云图、最大径向应力云图、最大位移云图以及最大应变云图分别如图3~7所示。
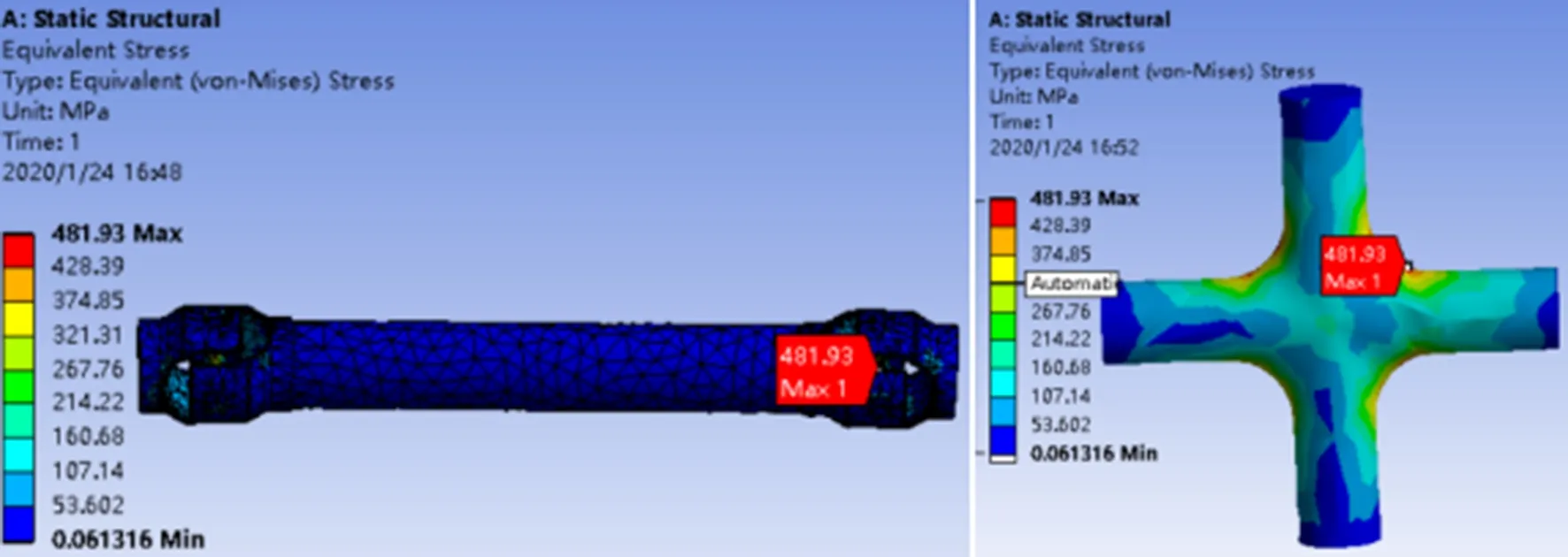
图3 最大等效应力云图Figure 3 Cloud chart of maximum equivalent stress
通过十字轴万向联轴器最大应力值云图得知,最大等效应力值为481.93 MPa,最大轴向应力值为136.95 MPa,最大径向应力值为423 MPa,其中最大等效应力值与最大径向应力值均出现在联轴器输出端十字轴轴颈过渡圆角处,最大轴向应力值出现在中间轴与十字轴连接处。根据机械材料四种强度理论可知,第一与第二强度理论适用于脆性材料,第三与第四强度理论适用于塑性材料。本次研究的十字轴万向联轴器强度分析中,所有零部件均属于塑性材料[4],所以研究采用第四强度理论,即:
(3)
式中,σ1、σ2、σ3分别为主应力;σs为材料屈服强度。
当σs除去安全系数s后,得到许用应力[σ],即[σ]=σs/s。
机械结构材料不被破坏,则其所受应力值应当小于其许用应力值。十字轴材料为42CrMo,其屈服强度值为950 MPa;中间轴材料为45钢,其屈服强度值为355 MPa。当安全系数s取1.9时,十字轴与中间轴的许用应力值分别为500 MPa和186.8 MPa,均大于万向联轴器各零部件所受最大应力值,表明万向联轴器满足强度使用要求。同时在最大位移云图中,最大位移值为15.8 mm,这是因为万向联轴器叉头与中间轴不在同一轴线,存在一定角度所致[5]。在最大应变云图中,最大应变值仅为2.39 μm,满足使用要求。
4 模态分析
模态分析是最简单的动力学分析,但具有非常重要的实用价值,可以帮助确定结构的固有频率和振型,从而使结构避免共振现象,并可预测结构在不同载荷作用下的振动形式[6],通过对十字轴万向联轴器进行模态分析,求解其固有频率与振型,分析其是否存在共振现象。
4.1 模态分析理论基础
当振动过程为无阻尼自由振动时,则公式(1)转变为无阻尼系数的微分方程,即:
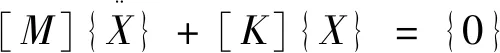
(4)
由于自由振动为简谐振动,则式(4)转变为:
([K]-ω2[M]){δ0}={0}
(5)
式中,{δ0}为自由振动总体振幅列阵;ω为固有频率。
4.2 模态分析
在ANSYS Workbench中采用Modal模块进行模态分析,模态分析过程与静力学分析过程相似,同样需要设置材料属性、零部件间接触类型、网格划分、施加约束等。在进行模态分析时,对万向联轴器两端叉头施加固定约束,模态提取方法设置为程序自动控制,其余材料属性、接触类型以及网格划分均与本次静力学强度分析相同。通过模态分析得出十字轴万向联轴器前五阶固有频率见表2,前四阶振型如图8所示。

表2 前五阶固有频率Table 2 Natural frequencies of the first five phases
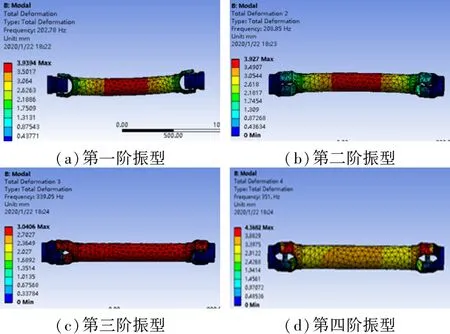
图8 十字轴万向联轴器前四阶振型Figure 8 Vibration shapes of the first 4 phases for cross shaft universal coupling
通常,稳定运行的电动机额定转速为1500 r/min,经过减速箱调速后,其转速一般在50~200 r/min之间,对应的转动频率为0.83~3.33 Hz,远小于万向联轴器的一阶固有频率202.78 Hz,因此不会发生共振现象。
5 结语
通过对十字轴式万向联轴器进行静力学强度分析与模态分析之后,得出如下结论:
(1)最大等效应力值出现在十字轴轴颈过渡圆角处,因为十字轴为万向联轴器中实现变角度以及传递动力的关键部件,最大应力值为481.93 MPa,小于其许用应力值。同时在十字轴轴颈处出现应力集中现象,与十字轴常见损坏部位相同。最大轴向应力与最大径向应力分别为136.95 MPa和423 MPa,均在许用应力范围之内,表明十字轴万向联轴器各零部件均满足强度要求。
(2)在整个十字轴万向联轴器装配体当中,受力最小的零部件为中间轴,表明中间轴有较多的冗余材料,可适当对中间轴进行优化设计,在满足强度使用要求下,节省中间轴材料,节约制造成本。在最大位移云图和最大应变云图中,最大位移值为15.8 mm,最大应变值为2.39 μm,均满足使用要求。
(3)通过对十字轴万向联轴器整体进行模态分析,得出其前五阶固有频率与前四阶振型,其中十字轴万向联轴器转动频率为0.83~3.33 Hz,远小于其一阶固有频率值,表明十字轴式万向联轴器不会存在共振现象。
