某电动SUV后扰流板气动特性的研究
2020-10-09李现今李喆隆
李现今,李喆隆
(北京新能源汽车股份有限公司,北京 100176)
前言
汽车在高速行驶中,来自空气的作用力会对汽车产生很大的影响,气动阻力影响汽车能耗,气动升力影响行驶稳定性。据统计,当车速达到80 km/h时,50%左右的动力输出用于克服空气阻力。通过降低风阻来降低能耗提高续航里程,对于电动汽车的意义尤其重大。另外,在高速状态下,如果气动外型设计不好,升力过大,将对汽车的行驶安全造成一定影响。之前,有很多关于汽车标模MIRA模型的气动力研究[1-6],但大多局限于对标模或者一般轿车的气动力研究,而缺乏对高速行驶的SUV车型的气动力研究。文献[7]中就面包车尾部造型对其气动特性的影响做了研究,文献[8]和文献[9]中对汽车底部流场做了研究,文献[10]和文献[11]中分别对俯仰运动和非定常运动对升力的影响做了研究,文献[12]中对汽车前、后轴的升力情况作了研究。本文中针对高速行驶的电动SUV的后扰流板上表面倾斜角度、开孔大小和形状对整车气动阻力和升力的影响进行了研究。首先,针对该电动SUV车型的基础状态,通过雷诺时均的Realizable k-ε、Standard k-ε、SST k-ω、Standard k-ω、Reynold stress和Spalart-Allramas等6种湍流模型,在车速为120 km/h的工况下进行整车外流场仿真分析,并将气动阻力系数和升力系数与等比例油泥模型风洞试验结果对比,结果显示Realizable k-ε湍流模型仿真和试验的差异最小。接着采用Realizable k-ε湍流模型对后扰流板气动性能进行仿真。针对该SUV的后扰流板上表面倾斜角度对整车气动升阻力系数的影响,优化了后扰流板的倾斜角度;并针对该SUV的5种后扰流板结构进行仿真分析,根据风阻系数和气动升力系数,得到最优状态的后扰流板结构。在验证试验中,优化后风阻系数下降了3.9%,升力系数有所上升,但在可接受范围内,有效地降低了整车能耗,提高了续航里程。
1 理论基础
1.1 计算模型与网格
计算模型为整车模型,含有平整的底盘护板,前机舱部件齐全,主动进气格栅处于关闭状态,模型如图1和图2所示。计算体网格采用Trim网格,边界层采用6层网格,总厚度2 mm,总网格量为3千万个。

图1 整车侧视图

图2 整车底视图
1.2 计算方法概述
对流场的仿真方法有:直接数值模拟(direct numerical simulation,DNS)、大涡数值模拟(large eddy simulation,LES)和雷诺平均数值模拟(Reynolds averaged Navier-Stokes,RANS)和格子玻尔兹曼方法(lattice Boltzmann method)等[13]。
1.2.1 DNS方法
由于N-S方程本身是封闭的,故从原则上可直接求解所有湍流问题。用DNS方法直接求解N-S方程,能获得最精细的流场信息。但该方法计算量特别巨大,对软硬件均要求较高,只适合简单的模型,对整车这样复杂的模型仿真无法实现。
1.2.2 LES方法
LES的基本思想是:把湍流瞬时运动通过某种滤波方法分解为大尺度运动和小尺度运动两部分。大涡运动通过直接求解N-S方程计算;小涡运动的影响概化为亚格子雷诺应力,须通过建立模型求解。
1.2.3 RANS方法
由于雷诺平均方程是不封闭的,故RANS的核心思想是建立雷诺应力封闭模型,使平均运动方程可解。目前比较常用的RANS模型有零方程模型、一方程模型、二方程模型和代数应力模型。RANS方法比前两种方法大大减小了对计算机硬件的要求,是目前车辆工程界处理湍流问题的最常用方法。
1.2.4 格子玻尔兹曼方法
从分子动力学的玻尔兹曼方程出发,可推导出空间和时间离散的格子玻尔兹曼方程,该方程的低阶形式收敛为Navier-Stokes方程。该方法直接模拟湍流的计算量也难以接受,而将格子玻尔兹曼方程同大涡模拟的方法相结合,能以可接受的计算资源量模拟湍流,并获得很高的精度。但目前该方法的商用软件十分昂贵,本文中不予采用。
2 湍流模型的确定及其仿真与试验
针对该电动SUV车型在车速为120 km/h工况,采用STARCCM+软件,通过有限体积的RANS方法,分别以Realizable k-ε、Standard kε、SST k-ω、Standard k-ω、Reynold Stress和Spalart-Allramas(SA)等6种湍流模型进行整车外流场仿真分析。Realizable k-ε计算结果的速度云图和速度等势面图如图3和图4所示。为验证仿真结果,同时进行了基础状态的等比例油泥模型风洞试验。

图3 速度云图(y=0)

图4 速度等势面图
2.1 气动阻力仿真结果
计算大约在2 000步时达到稳定,总共迭代3 000步,取2 500~3 000步的平均值作为气动系数。计算的风阻系数Cd结果见表1。
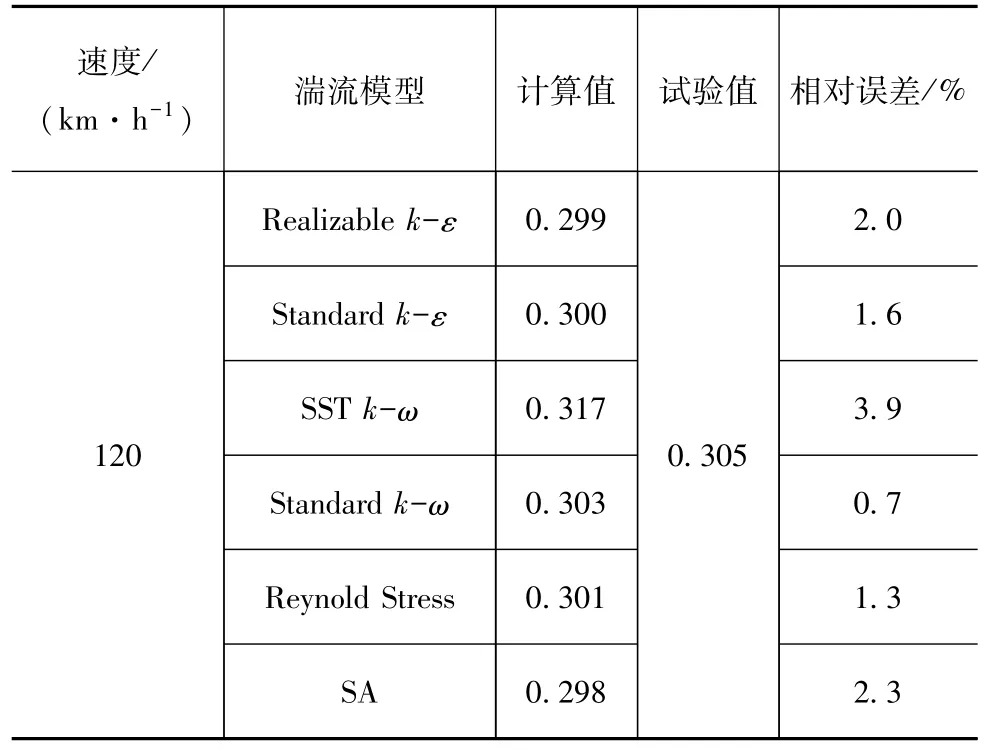
表1 C d计算与试验结果的比较
从表1可以看出,在阻力系数的计算中,SST kω的结果与试验的偏差略大,其它湍流模型所得仿真结果与试验值相对误差在2.5%以内。
2.2 气动升力仿真结果
气动升力系数Cl计算与试验结果的比较见表2。从表2可以看出,在升力系数的计算中,各种湍流模型所得仿真结果与试验值相对误差比阻力系数的大,最多相差40%。
综合表1和表2的结果看,采用Realizable k-ε湍流模型时误差较小。因此,后续的外流场仿真优化中采用Realizable k-ε湍流模型。
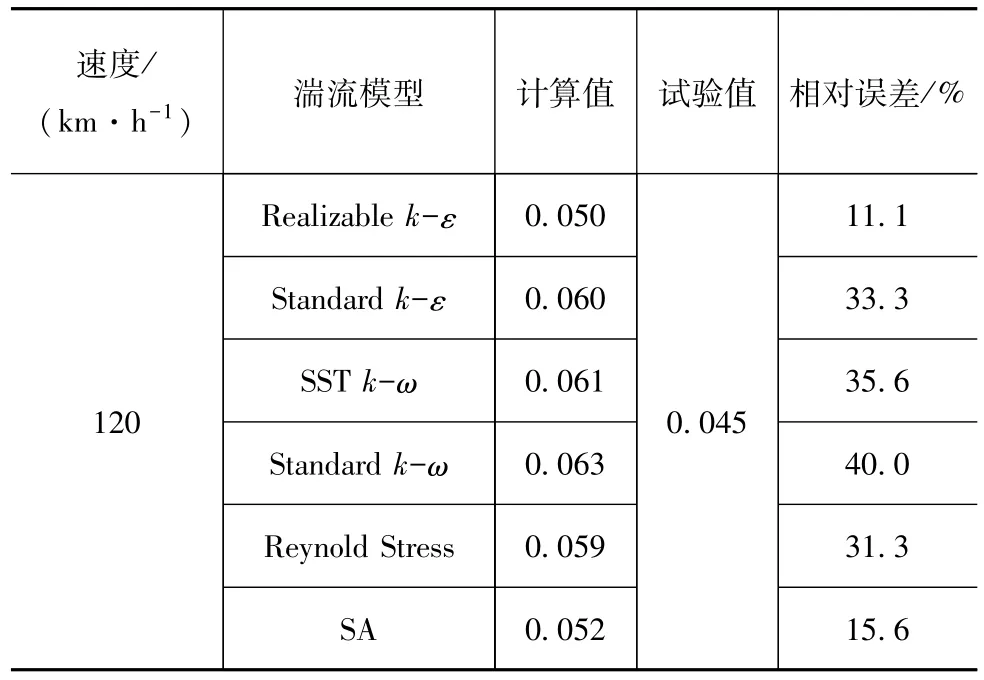
表2 C l计算与试验结果的比较
3 后扰流板的优化
3.1 后扰流板旋转方案优化
后扰流板的外观如图5所示,而图6则示出其对称截面中线形状和初始方位。该款SUV的后扰流板第1种优化方案是在图6所示初始方位的基础上,使后扰流板绕其前端中点而与车身常用坐标系的y轴平行的轴线旋转1°至6°,间隔1°,如图5所示,分别进行整车外流场仿真,观察其气动系数的变化,结果如图7所示。

图5 后扰流板外观图

图6 后扰流板对称截面中线形状及其初始方位
由图可见:随着后扰流板旋转角度的变化,阻力系数先降后升,在4°时达到最小值;而升力系数则先升后降,在4°时达到最大值。综合考虑升、阻力系数的变化,认为旋转4°时为最优的状态,风阻系数为0.294,通过速度云图(图8)可以看出,优化后气流从后扰流板分离后,沿着后扰流板上表面方向的低速气流延伸得更远,尾涡更加稳定,使整车风阻更低。

图7 后扰流板旋转角度示意图

图8 后扰流板旋转优化前(左)后(右)附近流场示意图
3.2 后扰流板开孔方案分析
第2种优化方案是在扰流板上开通孔。在最优的4°倾角的后扰流板基础上,设计了5种后扰流板开通孔方案,如图9所示。

图9 后扰流板5种开孔方案示意图
5种方案均具有两个对称的气流入口和出口。方案1和方案2的通道出口长度为265 mm,不同在于方案2的出口略微上抬。方案3、4、5的出口长度均为200 mm,方案3为在方案2的基础上,两入口Y向两侧各减小32 mm,方案4为在方案2的基础上两孔内侧减小65 mm,方案5为方案2出口200 mm,出口的上部不变,下部略微上抬。
后扰流板通孔和不通孔的差异,体现在图10和图8速度云图中后扰流板附近气流的差异。仿真的数据如图11所示。可以看出:阻力方面,由于后扰流板通孔后有气流补充进了尾涡区,加强了尾涡区空气的流动,空气受到的阻碍减弱了,5种通孔方式对应的风阻系数从通孔前的0.294减小了0.002~0.008,效果最好的方案5风阻降至0.286;升力方面,由于气流从通孔斜向下流动,说明这部分气流比没有通孔时的流动额外受到了向下的作用力,即汽车会受到空气向上的升力,从整体上看说明气流从车辆上方的绕流更多,也类似于机翼上升原理,翼型上方的绕流越多升力越大,因而通孔后的升力系数比通孔前0.06的水平显著提高了0.030~0.039。

图10 方案1(左)和方案2(右)的速度云图
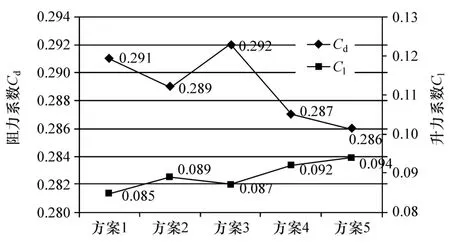
图11 5种通孔式后扰流板的风阻、升力系数对比图
不同形式通孔之间的差异,从图12和图10的速度云图可以看出:方案4、5的气流从后扰流板分离后,沿着后扰流板上表面方向的低速气流延伸得更远,低速区和上方高速区的边界更清晰光滑,尾涡更加稳定,使整车风阻更低;升力方面,由于通孔附近的气流方向为下后方,如果气流向后向下的局部流动得到加强,说明车辆向前向上的受力小幅增加,即风阻小幅减小,升力小幅增加。
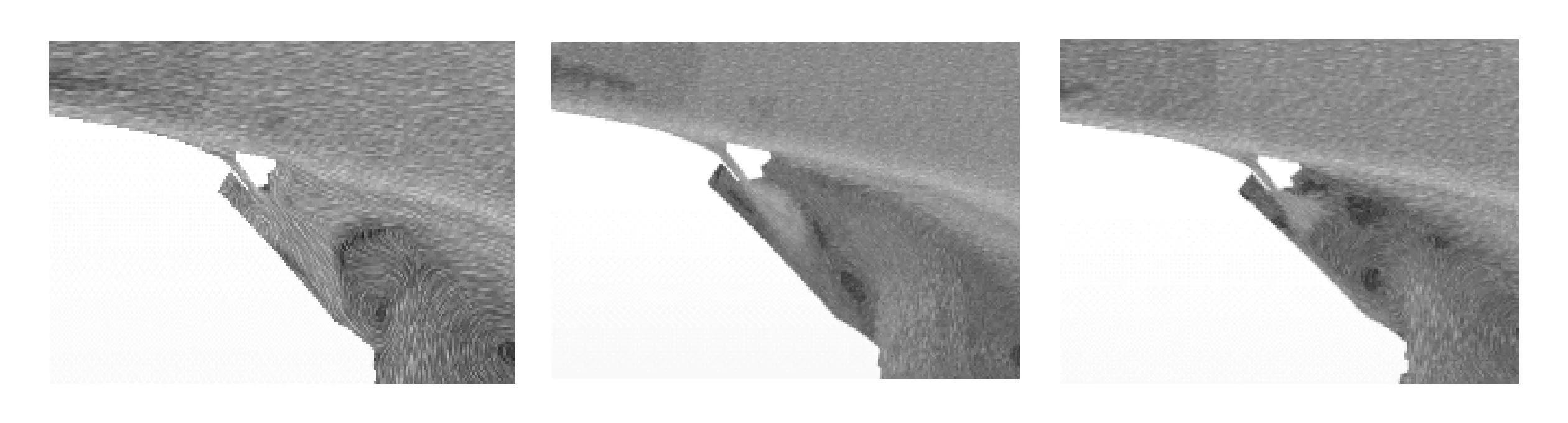
图12 方案3(左)、方案4(中)和方案5(右)的速度云图
通过仿真优化后的后扰流板,采用风阻最小的方案5在风洞中进行验证试验(图13)。测试结果:风阻系数为0.293,升力系数为0.083,如图14所示。风阻系数比优化前降低了约3.9%,升力系数大幅增加,约增大了84%,但仍在工程接受范围内;风阻系数仿真值比试验值约小2.4%,升力系数仿真值比试验值约大13%,吻合较好。说明仿真手段对于该电动SUV后扰流板的气动特性开发是有效的。

图13 后扰流板的风洞试验图
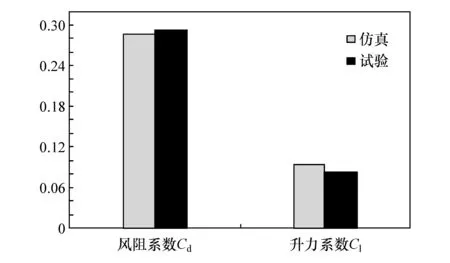
图14 升、阻力系数仿真与试验对比图
4 结论
本文中采用雷诺时均方法,对在120 km/h车速下某款纯电动SUV车型进行整车外流场仿真分析,得出如下结论。
(1)分析了该SUV的后扰流板上表面不同倾角对整车风阻系数、升力系数的影响,在基础状态上后扰流板上表面旋转4°时风阻系数最小。
(2)在最佳倾角的基础上,对后扰流板5种通孔方案进行对比仿真,结果第5种方案的风阻系数最小,故选取它为最优方案。
(3)以转角4°和第5个通孔方案为后扰流板的最优状态,在风洞试验中进行验证,结果表明气动阻力降低了3.9%,而升力系数虽有较大的增加,但仍在合理范围内。
