“顺”势而为，“破”而后立，让学习真正发生！<br/>——对“三角形三边关系”的教学思考

“顺”势而为，“破”而后立，让学习真正发生！
——对“三角形三边关系”的教学思考

2020-09-28江苏泰兴市黄桥小学教育集团十桥校区徐希浩

小学教学研究 2020年28期

江苏泰兴市黄桥小学教育集团十桥校区蒋娜徐希浩

一、“顺”学生思维，让学生研究指向更清晰

对于“能围成”与“不能围成”的呈现次序，我们数学团队也进行了讨论。部分教师觉得，应该先研究能围成的情况，因为学生学习知识，要先给他正确的。也有教师坚持认为，应该先研究不能围成的情况。只有弄明白为什么“不能围成”，学生的探索才会指向三角形三边的关系，从而真正理解为什么“能围成”。

为了厘清认识，研究小组的周老师和汪老师进行了同课异构的教学。为了便于比较，两节课堂上，均为学生提供2厘米、4厘米、5厘米、8厘米的小棒各一根，均采用小组合作的形式，任选3根小棒，围一围，再把每次围的情况记录在表格中。

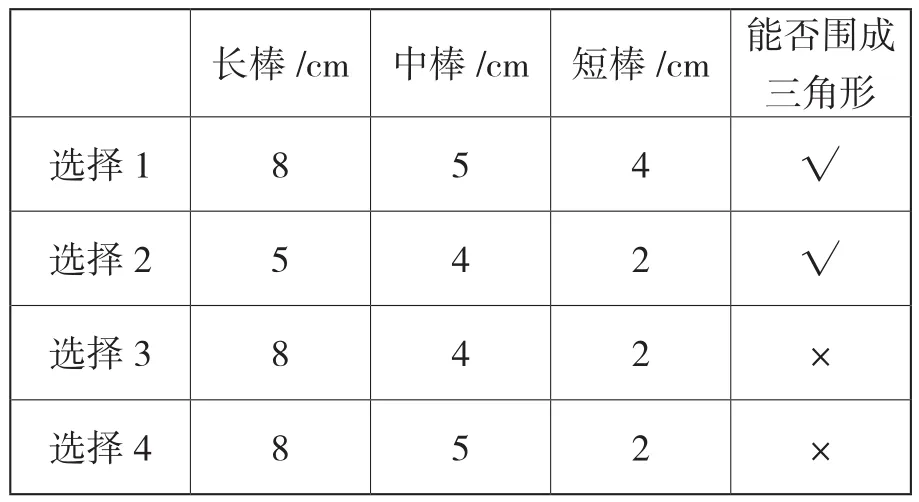
长棒/cm 中棒/cm 短棒/cm 能否围成三角形选择1 8 5 4 √选择2 5 4 2 √选择3 8 4 2 ×选择4 8 5 2 ×

【周老师课堂片段】

师：请同学们观察能围成的两种情况，它们为什么能围成三角形呢？

（学生一脸茫然，由于没有经验，他们根本不会想到把两边之和与第三边进行比较）

师（提醒）：你们可以把两根小棒的长度加起来与第三根的长度比一比，看看有什么关系。

（在教师的提点下，学生配合照做，但嘴里嘀咕声不停：这样比是什么意思？为什么要这样比呢？老师怎么想到的？学生虽然也在计算，也在操作，但脸上的茫然一直未消失）

……

这样教，也得出了“三角形两边之和大于第三边”的结论，但学生过于被动，过程牵强。

【汪老师课堂片段】

师：对于刚才围三角形的过程，你们有什么想问的吗？

生：为什么有的能围成三角形，有的却不能围成呢？

课件集中呈现不能围成的图形：

师：是呀，为什么有的情况围不成三角形呢？

生1：上面两条线段太短了，够不着。

生2: 2＋5＜8，2＋4＜8，两条边加起来都比8厘米短，所以围不成三角形。

师：要想能围成三角形，你能想出什么好办法？

生：可以把短线段加长一点！

（课件动态演示：将图①中的2厘米加长为3厘米）

师：根据你们的建议，把短线段加长了，现在能围成吗？为什么还是不能围成？

生：两条短线段的和刚好等于8厘米，这样就“拱不起来”，还是不能围成三角形，应该再加长一点。

（课件动态演示：3厘米继续加长为4厘米，能围成三角形了）

生3：老师，我还有方法能围成三角形。除了可以把上面两条短线段加长，还可以把下面一条长线段缩短。

（课件动态演示：把图①的8厘米缩短为6厘米，能围成三角形）

师：同学们通过观察和思考，发现了“从不能围”到“能围成”的解决方法，无论是把短线段加长，还是把长线段缩短，目的都是什么？

生：让上面两条线段的和大于第三条线段。

师：回顾刚才的过程，你们认为三条线段什么情况下不能围成三角形，什么情况下能围成三角形？

生：当两条线段之和小于或等于第三条线段时，不能围成三角形；两条线段之和大于第三条线段时，才能围成三角形。

……

对比两位教师的教学过程，我们认为第二种教法更符合学生的认知规律，更能顺应学生的思维递进，学生探究的欲望更强，理解更顺畅。面对能围成和不能围成，学生首先质疑的是：为什么有的不能围成三角形呢？通过观察，学生注意到，上面两条线段太短了，“够不着”，要把三条线段“拱起来”。围成三角形，得把上面的短线段加长，或把下面的长线段缩短。学生寻觅到了“不能围成”的根源，也就很自然地想到把上面两条短线段的和与第三条线段比较，完成了从“两根线段之间比长短”到“两条线段的和与第三条线段比大小”的思维跨越。

但教学到此，学生的思维也往往会停顿在“上面两条线段的和与下面线段的比较”上。不及时打破这种定式，把学生从局限中拉出来，学生会由于认识的片面、肤浅，从而无法完成对三角形三边关系的完整建构。