小学数学“解决问题”能力测评实证研究

浙江杭州市江干区教育发展研究院 潘红娟

解决问题究竟需要哪些能力？如何通过评价，使解决问题能力结构清晰化，是当前小学数学“解决问题”教学研究中亟待破解的重要命题。

前期，笔者团队以“解决问题能力测评与教学”为主题展开实证研究，试图通过对教材各年级“解决问题”的例题分析，对各年级理应达成的能力水平进行细化分解。从中观层面，对各年级学生解决问题能力水平进行测评，并借助测评为教学提供导向与参考。

一、命题设计与测评实施

1.测评框架与指标设计

依据解决问题的一般过程，我们可以理解为完整的解决问题是一个信息梳理、问题识别、关系表征、拟定计划、策略运用、方法确定和回顾反思的过程。既然学生需要经历这些步骤，那么，相应的能力便成为问题是否顺利解决的关键，也便成为“解决问题”测量与评价的重要指标。

我们参照人教版数学教材解决问题例题编写的三个模块，即“阅读与理解” “分析与解答”和“回顾与反思”，将这种过程性的能力转化为更具体的15个二级能力指标，然后对每一个指标的能力水平要求进行详细描述。这样的指标细化，不仅为能力测评提供较为明确的依据，也为能力培养提供了明确的方向。

2.试题编制与说明

依据下表中的能力要素进行试题编制，具体试题将在文中结合测试结果加以阐述。值得说明的是，在编拟试题时，考虑到“解决问题”内容所具有的综合性特征，每一个测评试题与能力指标间并不存在一一对应的关系，一般会有这样几种情况：①一个测试材料指向多个能力指标；②一个测试材料重点指向一个能力要点；③部分能力指标用多个材料测试；④测试材料并不覆盖解决问题能力体系的全部指标。

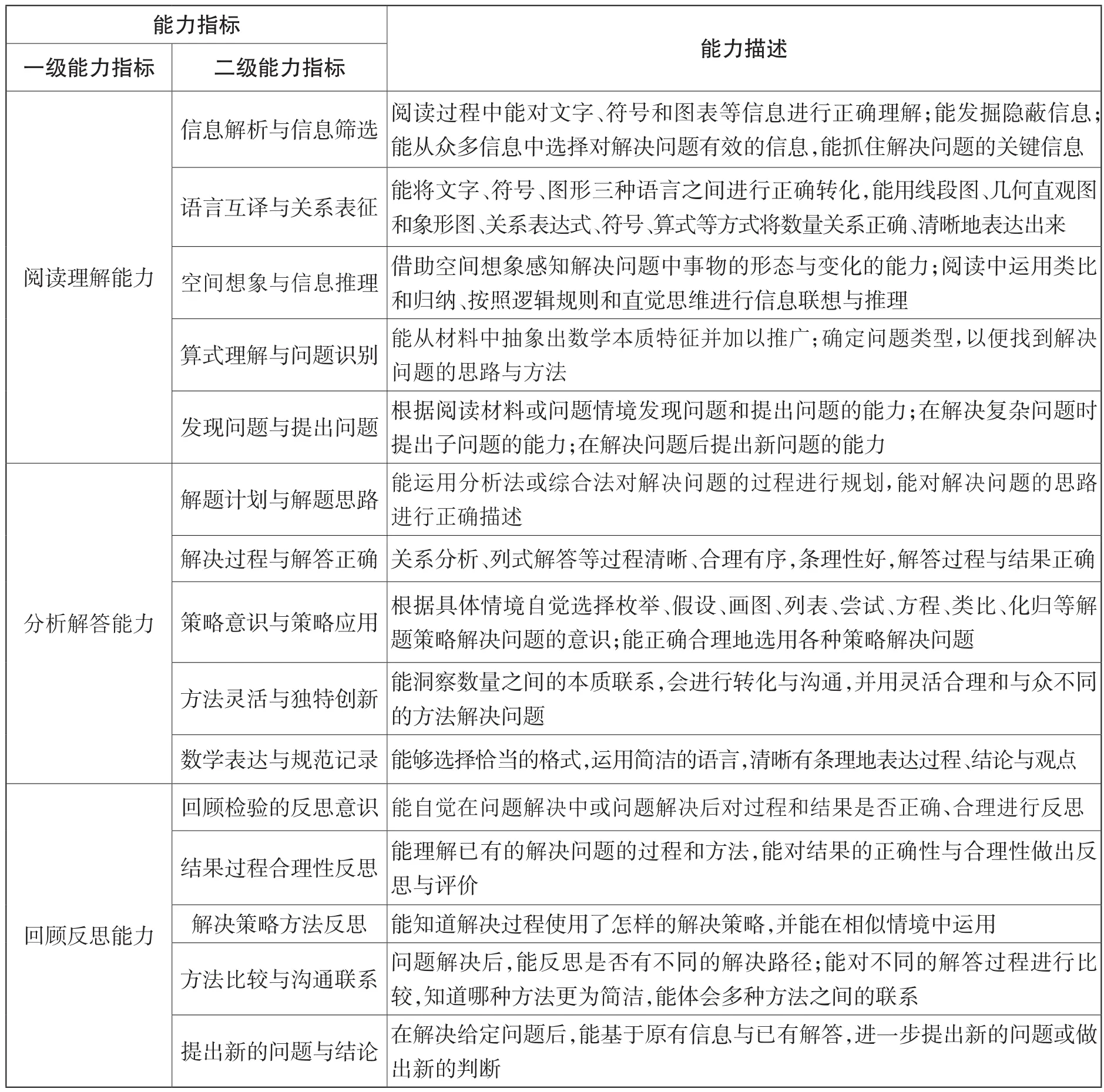
解决问题能力结构分解及其具体能力描述

3.测评样本与实施办法

本次测试对象为五年级学生，样本来自杭州市某区27所学校，样本类型涵盖农村学校、民工子弟学校和城镇学校，样本总量为6521人。

“解决问题”能力测评以人教版数学五年级上册教学内容为知识技能基础，主要内容包括：小数乘法、小数除法、简易方程、多边形面积、植树问题等。测试与阅卷由区教育发展研究院统一组织，测试组织严密，网络多轮阅卷，数据真实有效。

二、试题例举与情况分析

1.“阅读理解”能力情况分析

（1）信息解析与筛选整合

“信息解析与筛选整合”能力具体是指在阅读过程中能对文字、符号和图表等信息进行正确理解；能发掘隐蔽信息；能从众多信息中选择对解决问题有效的信息；能抓住解决问题的关键信息。

【测试材料1】据媒体报道：

2019年9月，各省猪肉价格大致相同，约为28元/千克。至2019年12月，我国猪肉价格持续上涨，华东地区大部分省份猪肉价格比9月上涨了6元/千克。其中浙江的涨幅更是逼近7元/千克，北方地区的陕西省涨幅为5元/千克。

杭州某小学食堂12月要购进猪肉40千克，如果按9月的猪肉价格，不改变预算，这笔钱能购进猪肉多少千克？

【测试材料2】下面是某专车的收费标准：

舒适型价格：14元（起步费）+2.6元/千米（里程费）+0.5元/分钟（时长费）

商务型价格：20元（起步费）+3.5元/千米（里程费）+0.8元/分钟（时长费）

李老师要坐该专车去某地，百度地图搜索信息如下：

如果按最省时的方案，李老师到达目的地至少需要付费多少元？

【分析】试题均给出信息多元、呈现方式多样的真实情境，考查学生能否获取有效信息，进行数学运算与问题解决。题1正确率为78%，区分度为0.54，题2正确率为68%，区分度为0.53。从结果可见，①学生具有较好的信息筛选意识；②与纯文本信息相比，对于用图、表、文字等综合文本呈现的真实情境，学生的解读与筛选能力较弱。

（2）语言互译与关系表征

问题表征是指问题解决者在阅读过程中将外部信息转化为内部信息，明确问题给定的条件、目标和允许的操作，是对具体的问题信息进行感知提取、理解内化、转换表达的认知过程。具体表现为能用线段图、几何直观图、象形图、关系表达式、符号、算式等方式将数量关系正确、清晰地表达出来。

【测试材料3】奇奇和格格玩游戏，奇奇在A处，格格在B处。游戏开始，他们分别从相距20米的A、B两地同时沿直线向同一个方向的终点跑去，20秒后奇奇追上格格，已知奇奇跑的速度是6米/秒，格格跑的速度是每秒多少米？（请用线段图表示题目的意思，并解答）

【测试材料4】微信朋友圈中有一个“一元钱去哪了”的小故事：

小明向爸爸妈妈各借钱50元，买书用了97元，剩下的钱，各还父母一元，还欠父母各49元，自己还剩下1元。他算了一下：49元+49元=98元，98元+1元=99元。小明觉得很奇怪，还有一元去哪了？

你觉得小明错哪了？根据这个故事情境，请你写出两个正确的等量关系：

向父亲借的钱+向母亲借的钱=买书的钱○ （ ）

欠父亲49元+欠母亲49元=（ ）○（ ）

【分析】试题3，给出教材不曾出现的行程问题类型，重点考查学生利用线段图进行关系表征的能力；试题4利用微信故事作为背景，考查学生用关系式进行问题表征的能力。“线段图表征”题得分率为62%，“关系式表征”题得分率为67%。从测试结果分析，在未曾见过的新问题解决中，学生无论是用直观图，还是用关系式表征题意的能力均有待加强。

（3）空间想象与信息推理

【测试材料5】右图四边形ABDE是一个直角梯形。

如果AE=x，DE=5，∠ABE=45°，CD=3，那么梯形ABDE的面积是（ ）。（用含有字母的式子表示）

【分析】本题考查信息筛选与信息推理的特征十分鲜明。难点一，“ED=5”是多余信息需要排除，难点二，高的长度需根据45°直角三角形推理获得。此题得分率仅为 56%，区分度为0.52。通过对学生的访谈我们发现，在图形问题的解决过程中，学生具有信息筛选的意识，但信息推理的能力相对较弱，学生对于高的信息的推理存在困难。

（4）算式理解与问题识别

“算式理解与问题识别”是指理解解决问题的思路和算式的意义，根据方案、算式等找到相应的具体问题。

【测试材料6】下面问题中，不能用算式“400-75×5”解决的问题是（ ）。

A．奇奇家和格格家相距400米，奇奇的速度是75米/分，格格的速度是65米/分，两人同时从自己家向对方家出发，5分钟后，奇奇离格格家还有多少米？

B．带400元钱去买球，足球单价75元。买了5个足球后，还剩多少元？

C．小明参加跳绳比赛，6次的总成绩是400个，其中前5次的平均成绩是75个。小明第6次跳了多少个？

D．要生产400个奥运会吉祥物，5天生产了75个。还剩多少个没有完成？

【分析】此题编拟了行程问题、购物问题、工作问题、平均数问题四个不同的情境材料，意在根据运算意义，找到与算式相符的应用情境。此题得分率仅为48%，区分度为0.59。A、B、C、D各选项比例分别为31.6%、2.66%、18.07%、47.67%，其中错误选项A的选中率高达31.6%，由此可见，学生算式理解与问题识别的能力有待提高。

2. “分析解答”能力情况分析

（1）策略意识与策略应用

问题解决的程序固然重要，但起关键作用的还是解决问题的策略。学生能否主动选择画图、方程、分类、化归、例举、逆推、列表等策略和方法，是解决问题能力高低的重要标志。

【测试材料7】爸爸皮夹里有一些100元和50元的人民币纸币，可可帮爸爸数了一下，发现皮夹里共有2000元，而且100元纸币的张数正好是50元纸币的2倍，爸爸皮夹里共有几张纸币？

【测试材料8】周长为300米的圆形池塘边均匀地栽了10棵柳树，在每两棵柳树之间均匀地栽了5棵桃树，每两棵桃树之间的距离是多少米？（建议画图）

【分析】材料7，重点考查学生在没有提示的前提下，能否自主运用方程来解决问题。此题得分率为65%，区分度为0.72，学校之间差异大，学校得分率最低的仅为51%。此题等量关系清晰，如若用方程解决，将会大大提高问题解决的成功率，而正确率不高的原因，主要是学生方程策略意识的薄弱所致。

材料8，“植树问题”的教学意义，不是一类问题的解决方法，而是几何直观的策略应用与模型思想。本题的核心宗旨正是考查学生能否运用“画图”分析问题，得分率仅为49%，区分度为0.59。说明教师在本内容的教学中，过于重视基本模型的获得与运用，忽略了“思想方法与策略应用”的目标定位与能力要求。

（2）方法灵活与独特创新

【测试材料9】2019年12月16日24时，油价调整最新消息。

浙江油价表如下：

89号汽油 92号汽油 95号汽油 0号柴油价格（元/升） 6.59 7.1 7.56 6.74

李师傅的车只能加92号汽油或95号汽油，如果李师傅加了36升汽油，付300元够吗？付250元够吗？

【分析】“油价问题”的正确率为93%，从学生答题情况分析，正确率高的同时，也反映出学生解决方法的多样性。

“方法灵活与独特创新”这一能力指标，并不依赖一个试题获得结果。上文材料7“皮夹中的纸币问题”中，解答情况也极好地彰显了学生个性化的思维与多样化的解决策略。

3.“回顾反思”能力测评与情况分析

（1）回顾反思意识

【测试材料10】王老师去超市买了0.84千克苹果，苹果单价是15.6元/千克，王老师实际付了（ ）元。

【分析】“求积的近似值”教学中，学生往往被明确指令“用四舍五入保留两位小数”，当这一指令不明确时，学生便显得无所适从。此题正确率为44.4%。从答题情况分析，反映出学生解决问题后“结果回顾”意识的缺失，缺少计算结果与问题解决（即实付金额）之间的转换。

（2）结果反思评价

【测试材料11】从A站到C站全程630千米。

求这个问题，乐乐是这样计算的：

乐乐做对了吗？请说明理由。

【分析】试题并没有用常规解决问题“条件—问题”的模式，而是给出解决问题的结果，让学生进行判断与说理。此题正确率为85%，学生能采用代入验算、估算检验、正确解答检验、关系说理等多种方法判断，从结果分析，学生能对情境和结果做出正确的判断与评价。

三、结论与启示

测评结果表明，学生解决问题能力中：1.面对有冗余信息的文本材料具有较好的筛选意识；2.在解决问题时策略的多样性方面表现较好；3.能对解决问题的结果进行合理地判断与评价。

测试也表明，学生在解决问题中表现出的能力弱项是：1.面对多样文本呈现的复杂情境，学生理解信息、筛选信息的能力较弱；2.解决图形问题时信息推理的能力有待加强；3.用图、表、关系式进行问题表征的能力有待加强；4.解决问题策略储备与经验缺乏，面对不同情境的问题主动选择有效策略的意识与能力较弱；5.对解决问题的结果进行回顾与反思的意识薄弱。

根据测试情况，教师有必要从以下方面予以重视与加强：

1.细化能力结构，将能力要素转化为具体目标导引教学

由于解决问题能力构成的复杂性、内隐性、过程性、综合性等特点，无论是教学评价还是教学本身都显得十分困难，难以把握。因此，将能力进一步分解细化，可以为教学提供具体方向。以“数学阅读理解能力”结构为例，可以细化为：概念理解、语言互译、抽象概括、空间想象、阅读推理、模式识别、阅读迁移、阅读元认知、信息筛选、信息整合等。只有将能力结构清晰化，才有助于目标的有效落实。数学阅读理解能力是这样，分析解答、回顾反思能力同样如此。限于篇幅，待后续讨论。

2.解读教材例题，在例题教学与能力培养之间建立深度关联

由于教材编写往往呈现内容显性、目标隐性的特点，导致教学中教师大多关注“短期目标”而忽视“长期目标”。从日常调研看，很多教师将会解这一类题作为最终目标，而并没有将解决问题能力培养作为目标加以重视。因此，教师有必要深入发掘每个例题所承载的能力目标点，只有在日常的例题教学与能力目标之间建立深度关联，能力培养才会落到实处。

3.梳理教材体系，蓄力完善解决问题能力培养的序列

我们发现，各版本教材虽已对解决问题教学十分重视，但尚无十分明确和完善的能力培养体系与序列。下图是人教版数学教材解决问题82个例题的分布情况，我们有必要分析思考。这些例题前后之间有怎样的递进与关联，是否存在基础性经验和策略性经验的断层，如何补上短板与断点，教学中如何依循能力结构中的每个能力点有序列地进行培养。

4.突破领域界限，关注其他领域学习对解决问题能力培养的作用

解决问题活动虽是一个相对独立的活动系统，但由于解决问题本身的开放性特点，决定了问题解决是否成功一定与问题解决者的数学基础知识、具体经验基础、数学思维基础、非认知因素基础等其他因素高度相关。因此，学生解决问题的能力发展并不完全依赖于“解决问题”领域内容的学习。教师有必要将“问题解决”教学与概念、法则、公式、定律等其他内容的学习紧密关联，一方面，深度理解这些知识以利于有效迁移应用；另一方面，以“问题解决”作为这些新知学习的驱动性任务和应用性任务，将解决问题能力培养浸润至数学学习的全部领域与内容之中。

5.深化课程理解，“解决问题不仅是一个领域，更是课程目标与理念”

据浙江省 2018 年小学教育质量监测数学学科能力测试的教师问卷统计，认为“新课程中的解决问题就是原来的应用题”，完全同意的教师比例占5.7%，比较同意的占29.6%；认为“解决问题的回顾与反思就是代入计算”，完全同意的占2.3%，比较同意的占10.6%，不确定的占8%。这些数据说明，教师对解决问题的课程理解尚待提升，教研部门、学校教研组有必要加强“解决问题”教学相关的项目研修，促进教师对这一领域课程目标的理解与教学策略研究。