基于SOLO分类理论的数学学习评价——以“整体建构”专题为例

江苏海安市城南实验小学 唐小琴 许卫兵

就小学数学学习评价现状而言，主要依据还是考试成绩，虽然在不少的学校也会考查学生的数学能力（如口算、操作、阅读等），但总体上，“一张试卷说了算”的情况还是比较普遍的。

本质上，“教—学—评”具有目标一致性。数学教育的基本目标是帮助学生学会思维，即我们应当通过数学帮助学生学会更清晰、更深入、更全面、更合理地思考。由于思维的内隐性比较强，因此，要考量思维发展的水平，则需要通过一定的形式将其“外显”，即通过外化行为洞察内在思维。这方面，SOLO分类理论为我们提供了一个很好的研究视角。

一、SOLO分类理论：可观察的学习成果结构

皮亚杰认为，儿童的认知发展有阶段性，从低到高依次为：

皮亚杰认知阶段理论重在表明：随着年龄的增长，人的认知结构会发生质的变化，年龄大的学生学习方式、思维水平在质上更加优异。

然而，有研究者提出，“上述有关发展阶段的假设并不成立”“仅仅是一个天才的假设”，原因是，“学生的表现不一定按这一顺序发展。……有的学生对某些问题的回答已经表现为形式运算，几个星期之后，对同样的问题却又表现为中级具体运算。”“哈勒姆（Hallam，1967）报告说，在历史科，心理年龄为10岁的学生对问题的回答有90%表现出前运算，也就是典型的5岁或6岁儿童所处的智力发展阶段。布莱克（Blake，1978）对一批澳大利亚的教育学院学生进行调查，发现其中有30%的学生在回答科学问题时的运算阶段和10岁的儿童一样”。

由此，彼格斯教授认为，“一个人在回答某个问题时所表现出来的思维结构，与这个人总体的认知结构是没有直接关联的。一个人总体的认知结构是一个纯理论性的概念，是不可检测的，是一种‘假设的认知结构’（Hypothetical Cognitive Structure），英文缩写为HCS。而一个人回答某个问题时所表现出来的思维结构却是可以检测的，称之为‘可观察的学习成果结构’（Structure of the Observed Learning Outcome），英文缩写为SOLO。因此，尽管很难根据皮亚杰的分类法认定学生处于哪一个发展阶段，但却可以判断学生在回答某一具体问题时的思维结构处于哪一个层次。”

SOLO分类理论由此产生。彼格斯提出思维分类结构也是一个由简单到复杂、由低级到高级的层次模型，共有五个层次：前结构、单点结构、多点结构、关联结构和抽象扩展结构。简单地讲，就是给学生一个问题，我们可以从学生的回答中看出他们的思维属于哪个层级。

相关层级结构的评定依据：

前结构（最低）：回答问题时，问题线索和解答混淆，逻辑混乱，或同义反复，拒绝、转换或跳跃到个别细节上，甚至连问题是什么都没有弄清楚。

单点结构（低）：回答问题时，只能联系单一事件，只接触到某一个点就立即跳到结论上去。

多点结构（中）：回答问题时，只根据几个有限的、孤立的事件进行“概括”，但由于基本上只注意孤立的素材，而使回答收敛太快，未形成相关问题的关系网络。

关联结构（高）：回答问题时，能够联想多个事件，并能将多个事件联系起来，建立起网络结构。

抽象扩展结构（最高）：回答问题时，能够进行抽象概括，结论具有开放性，使得问题本身的意义得到拓展。

这样的一种思维分类结构，和皮亚杰的认知发展各阶段的行为表现有很大的相似性。比照皮亚杰的认知发展阶段，就形成了SOLO分类层次表（见下页）。

需要特别注意的是，表中比照只是表明SOLO分类层次结构跟皮亚杰的发展阶段类似，体现了点、线、面、立体、系统的发展过程，思维结构越复杂，思维能力的层次就越高，但如果将二者等同起来就发生根本性错误了，其本质上的区别在于：认知发展阶段是就时间跨度而言的，而SOLO分类层次是针对某一个时间点而言的。此外，SOLO分类层次结构的研究更多用于开放式情境（问题），焦点集中在学生回答问题的“质”，而不是回答问题的“量”。传统的评价方式中，我们习惯把答案细分为若干个“采分点”来评分，“定量”评价的色彩更浓一点；SOLO评价不拘泥于学生答对了多少个与标准答案相近的字眼，更不局限在学生写出了多少个字，而是力求从学生的回答中分析出他能够达到哪一个思维层次。

二、SOLO分类评价的课例研究

整体性、结构性是数学学科的基本特点。近年来，我们努力通过整体建构教学来帮助学生完善认知体系，发展思维能力，培育思维素养，进而更好地理解数学，爱上数学，轻松地学好数学。那学生思维发展水平到底怎么样呢？如何评定呢？我们尝试着应用SOLO分类评价进行课例研究。

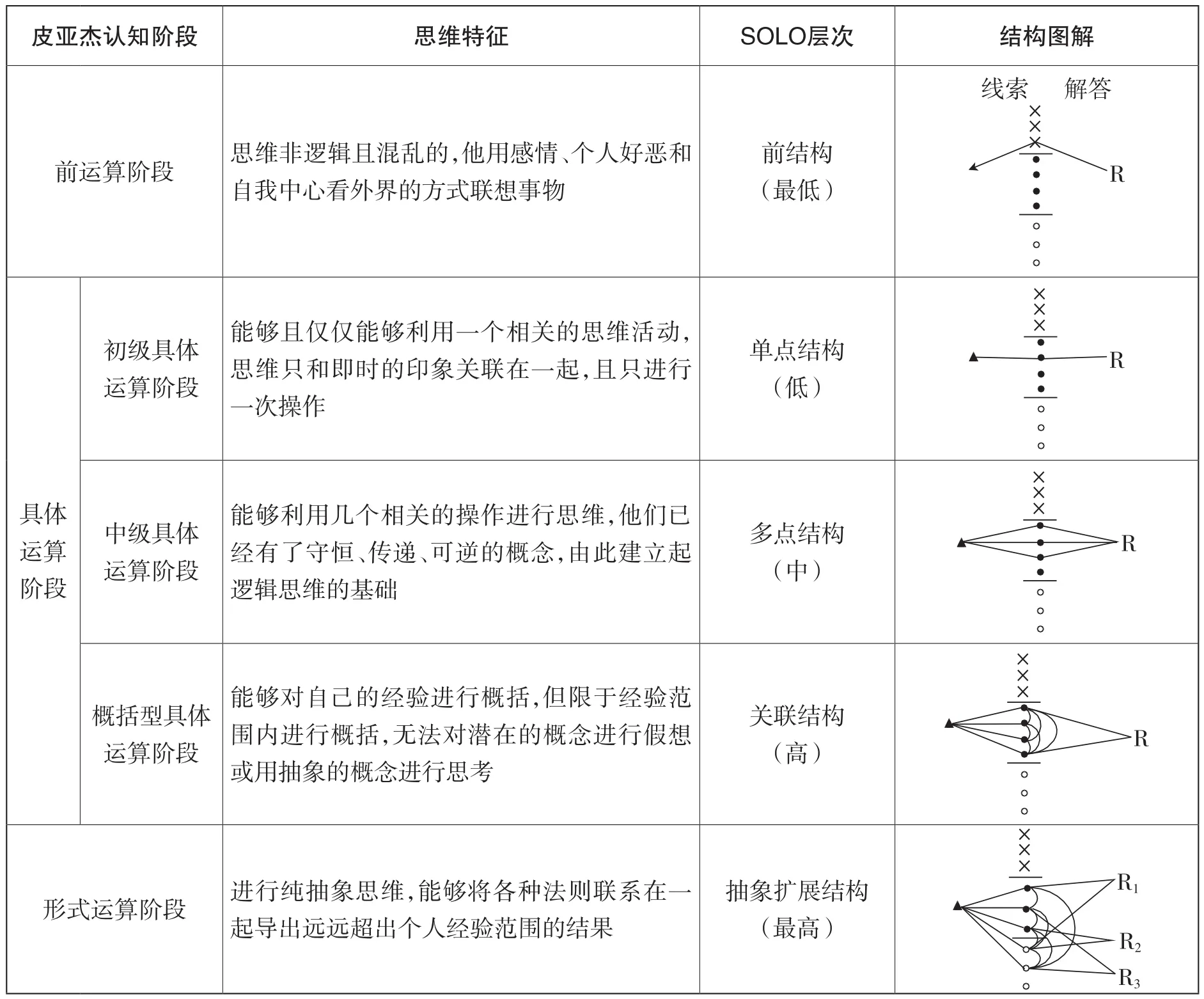
SOLO分类层次表

案例1：四年级《认识多位数》

1.教学描述

彼格斯教授指出，如果不熟悉学习过程、最初的意向和教学场景，评估者是不能做出判断的。因此笔者先借助板书，简单介绍这节课是如何整体建构的。

首先，从我们已经学过的计数单位导入，抓住十进制的关键——“满十进一”，从已学的“个”“十”“百”“千”自然生长出“万”“十万”等更大的计数单位。第二，根据学生的认数经验整体建构认数的研究方法：从数、读、写、组成这几个方面展开研究。第三，经历由繁到简的聚合性过程。学生一位一位地读写大数时普遍感到很麻烦，遵循“东西一多就要分类”的数学原理，学生围绕“怎么分”这一核心问题展开探究，最终确定“个、十、百、千”这四个计数单位是基本数级，“万、十万、百万、千万”好似复制出来的更高数级。“分级”使数的读写化繁为简。

2.样题设计

彼格斯教授发现，SOLO分类理论对开放题评分的信度高，能更准确、更客观地评价开放题，这也是SOLO分类评价理论获得广泛认同的根本原因。基于这样的指导思想，我们设计了如下检测单：

3.SOLO分类评价

被调查对象62人，对问题1的回答进行SOLO分类评价，思维结构呈现以下的情况：前结构2人，单点结构9人，多点结构41人，关联结构10人，抽象扩展结构0人；对问题2的回答进行评价，思维结构呈现以下情况：前结构0人，单点结构13人，多点结构42人，关联结构6人，抽象扩展结构1人。我们发现，大部分学生对这两个问题的回答在同一个或相邻的思维结构水平，只有极少数学生对这两个问题的回答思维结构水平相差较大。下面具体对学生第二个问题的回答进行SOLO分类评价分析。

（1）单点结构（13人，占比20.9%），如：

“汽车123500元，它是一个比一万还大的数。”

“长江长6397000米，读作六百三十九万七千米。”

这一类回答，结论只来自一个线索，他们觉得较大数就是比一万还大的数或者认识这个数只要会读就可以了。

（2）多点结构（42人，占比67.7%），如：

“我家装修用了34万元，34万写作340000，这是一个较大的数，如果我们要读出这个数，可以先分级，读作三十四万，末尾的四个0不要读。”

这个学生的回答，不仅关注了读数、写数，还关注到了0的读法，涉及多个方面，但这几个方面都没有建立关联，显得比较零散。

（3）关联结构（6人，占比9.7%），如：

“我家房子花费1250031元，首先这个数怎么读呢？也许你会读一百万、二十万、五万零三十一，这样一位一位地读非常麻烦，其实我们可以‘一级一级’地读，用小竖线在个级和万级之间分开，就是一百二十五万零三十一，这样就非常简便了。写数和读数一样都是从左往右。”

与多点结构回答相比，这个回答已经开始结合具体的问题情境，他不仅读出这个数，而且把一位一位地读和一级一级地读进行比较，由繁到简，这是一次概括。另外他还将读数和写数的顺序又进行了一次概括。

（4）抽象扩展结构（1人，占比1.6%）：

“我找到的数是100006，我从读、写、组成几个方面来介绍。首先这个数比较大，我们在读和写的时候要先分级，个、十、百、千属于个级，万、十万、百万、千万属于万级，读和写都是按照从左往右的顺序，读作十万零六（每一级末尾的零不读，中间的3个0只读一个零），写作100006，它是1个十万和6个一组成的。同学们，记住了吗？如果有一个更大的数100000006，该怎么读怎么写呢？同学们试一试。”

这一回答有如下特征：①整体把握研究认数的几个方面（读数、写数和数的组成等）这一概括性的认知可以运用各种数的认识；②根据已有的认知经验将较大的数进行了再一次扩展，当学生对较大数的理解发展到很高水平时，思维就会发生质的飞跃。

案例2：四年级《单式折线统计图》

1.教学描述

课始，教师创设检测保温杯效果的情境，让学生收集不同时刻的水温数据，整理成统计表，将统计表与制成的条形统计图进行比较，感受表与图各自的特点与联系；接着提问“除了用直条可以清楚直观地表示出某一个时刻的水温，你还能想到更简洁的方法吗？”学生通过点和线，经历由条形图生成折线图的过程；最后通过数据的分析，再次勾连、对比统计表和条形统计图以及折线统计图的特点与联系。整节课，抓住统计与概率的核心——用数据来“说话”，让学生经历了收集数据、整理数据、描述数据、分析数据的全过程。

2.样题设计

下面两幅都是2016年昆明市12个月的月平均气温统计图。比较这里的两幅折线统计图，它们有什么不同？想一想，气象台和旅游局为什么要分别用这两种折线统计图来表达数据呢？

3. SOLO分类评价

通过统计，调查对象共62人，运用SOLO分析理论分析学生解答问题时的思维结构呈现出以下四种情况（未出现抽象扩展结构）：

（1）前结构（1人，占比1.6%），如：

“因为我们这里下雨。”

这种回答是学生没有读懂问题的意思。

（2）单点结构（8人，占比12.9%），如：

“第一幅有数据，第二幅没有数据；第一幅左下角有锯齿，第二个没有；第一个让人看懂，第二个可以判断。”

这位学生的回答至少与问题相关，虽然回答的观点之间有重复，或很不一致甚至不正确，但还显示了一种低层次的浅表性思维结构。

（3）多点结构（45人，占72.6%），如：

“气象台一格是1℃（除了0～20），旅游局每格是5℃；气象台的折线上标了数据，旅游局的没有；两幅折线画的不同；气象台的折线忽高忽低，旅游局的折线基本是一条水平线。”

在多点结构的回答中，学生找出许多相关点。此时他们已经能从整体把握两幅折线统计图，感受到折线变化的程度不同，也看到了纵轴上一个单位长度表示的数量不同，但没有将这些相互联系起来看，更没有分析联想到气象台和旅游局采用这两种折线统计图呈现数据背后的原因。

（4）关联结构（8人，占比12.9%），如：

“第一个用1℃做一格的，第二幅用5℃做一格；第一幅0～20中的数都省略了，而第二幅没有；第一个看起来幅度较大，第二个看起来幅度较小；因为气象台数据要准确，是给市民用的，准确而且幅度大，可以更加提醒市民注意天气，旅游的人是看天气的好坏来旅游的，幅度小可以让游客放心。”

处于这一思维结构的学生在将分析的所有方面连贯成一个整体之后，还能做出关联性的分析判断，基于问题的背景下得出一个相关的结论。

综合以上两个案例分析，参照“认知发展的基本阶段和SOLO回答层次描述表”，10～11岁学生正常应处在多点结构思维水平，对照以上两个班级学生回答的SOLO分析数据，大部分学生均属于这一思维水平，还有近13%学生超过了正常水平，达到了关联或抽象扩展思维结构，这是一个不错的成绩。

当然，我们除了像上面这样通过对某一问题集体书面回答分层评价，也可以通过个体口头测试。相对而言，口述时学生会更加放松，语言表述也会较为自由，个体测试水平也会高于群体测试。

三、SOLO分类评价的反思

（一）收获

1.SOLO评价让教师的评价视角更开阔

很长一段时间以来，受分数定量评价影响，我们评价的视角比较单一，总喜欢把目光聚焦学生的错误回答，竭尽全力分析每一个错误回答背后的原因。然而在正确答案面前，很多时候却是答对即止，导致学生思维不深入，碎片化、单一化的回答比比皆是。SOLO质性分类评价提供一种新视角，促使教师将以评价对错为重心转移到学生回答的思维结构水平上，这对指导教学和评价学生的数学思维具有重要的现实意义。

2. SOLO评价让师生的整体建构更主动

教师借助SOLO评价结果可以有针对性地改进自己的教学，比如本班单点结构回答偏多，教师就会引导学生在多点结构层次获得更多更深的体验。为了使学生回答水平进一步向关联结构水平递进，教师在课堂上会主动尝试将多个事件关联起来，实现整体建构教学。作为学生，把他的回答和其他同学比较时，他们会寻找差距，找到自身回答存在的问题，并努力让自己达到更高层次的回答。这样看来，SOLO分类评价促进师生共同成长，整体建构意识也会进一步提升。

（二）挑战

SOLO分类评价指向于学生思维结构水平，测试题是否具有一定的开放性，是否能融知识、能力、思维、素养于一体，至关重要。像“4+3=？”这样直接得出一个结果，且所需要的工作记忆容量较少的，很具“单点结构”特质，检测效度就不高；像（4×2）□3=2，可以有多种思考方向，且运算过程前期得出的结果会影响后续的运算，就具有“关联结构”的特征。

SOLO分类各结构类型具有一定的特征，但区分的标准和界限并不十分清晰。因而，在面对同一问题的个性化且区分度不大的回答时，通常只能做一个大致的比较和相对划分，这也正说明SOLO分类评价存在局限性。为了提高准确性，我们需要设计与问题相匹配的要素表，把握不同要素的权重，并赋予不同分值，即将量化研究和质性研究相结合。

人的成长具有阶段性和规律性，同一年龄段的学生虽然在回答同一问题时会体现出思维水平的差距，但思维发展总体状况应该跟这个年龄段的儿童智能发展相吻合。因此，在进行SOLO分类评价研究时，也要考虑皮亚杰的认知发展阶段的相关理论常识，检测题的难度和开放度等也要与之相适应。

数学表达不仅是促使数学理解、数学思考走向深入的有效途径，更是深度学习的重要支撑，承载着分享观点、提升认识、发展能力的重要使命。但数学表达能力并不是天生的。我们应将“学生数学表达能力的培养”看作数学教育的基本目标之一，或看作努力提升学生必须具备的一种核心素养。因此，在学习中学会表达，在提升中发展思维，是我们应该坚守的初心。