基于Elman神经网络和Copula函数的多维装备效能评估模型

杨梓鑫，薛源，孙畅，徐浩军，韩欣珉

(1.西昌卫星发射中心，四川 西昌 615000；2.西北工业大学 航空学院，陕西 西安 710072；3.空军工程大学 航空工程学院, 陕西 西安 710038)

0 引言

空战装备作为空中作战体系的重要组成部分，合理准确地对其进行效能评估不仅可以反映武器装备实际使用效果，对开发论证起到辅助作用[1]，还可以推动航空装备研制技术的不断发展，为有关工业部门和战略决策层提供参考信息，因而一直是各国装备工作的重点[2]。但随着当代航空装备复杂度和空战信息化程度的不断提升，评估数据也逐渐呈现出非线性、多维性和耦合性等特征[3-4]。

针对评估数据的非线性特征，当前主流处理方法是以经典统计学理论将其简化至线性问题后进行求解，此种方法在数据量较大时会导致预测结果的波动性较大，对评估结构中的多动态性拓扑问题解决效果并不明显，当预测参数发生变化时，该方法过度关注系统局部特征而忽略预测趋势的缺陷开始逐渐凸显，预测精度也随之下降。近年来随着人工神经网络的兴起，将机器学习引入到对军事决策的分析中，从而获取待测装备关键指标权重的方法发展迅速。刘蜻等[4]通过建立径向基函数(RBF)模糊神经网络对某型装备进行效能评估；赵日强等[5]使用神经网络模型对装备费用效能不能定量描述的问题进行建模分析。但上述方法仅对一维的效能评估模型有所考虑，在面对多维耦合特性的评估数据时，尚有一定局限性。

而针对多维耦合特性数据的预测方法，军地双方学者取得了诸多研究成果。如：运用自组织映射(SOM)网络对不同型号的装备建立了效能评估分析模型[6]；通过提出敏感阈值、敏感后坐冲量两个评估概念建立多因素的机枪评估模型[7]；以北京市强降水频率尝试建立强降水致灾因素的多维变量联合分布模型[8]。这些文献从不同角度对多维耦合变量的预测评估问题进行了研究，但上述方法仍存在限制条件较多的问题，如需满足独立性假设、各变量服从相同边缘分布、多变量的联合分布服从正态分布或可以转化为正态分布等。

针对上述方法的缺陷，本文提出了一种基于Elman人工神经网络与Copula函数模型相结合的空战装备效能评估模型。针对现代化空中作战的特点，将空战过程划分为超视距和视距内两个阶段，并以此在文中构建了空战装备效能评估指标体系。利用神经网络分别对二者趋势进行预测后，针对其间的强耦合关系，运用Copula函数模型对变量间相关性结构进行构造，最终建立了空战装备效能的联合分布模型。并以Quantile Scoring(Q-S)方法和Central probability interval(CPI)指标为依据将本文提出的预测方法与传统方法进行对比，模型较原始方法精度有所提高，且无需对边缘分布类型加以限制，对武器装备效能的评估问题具有一定的参考价值，可为装备组合及新装定型提供分析和检验依据。

1 空战装备效能的边缘分布预测模型

1.1 空战装备效能的指标体系构建

本文空战装备效能指标体系以系统效能作为主要评估依据，在众多系统效能的评估分析方法中，选用20世纪60年代武器系统效能工业咨询委员会(WSEIAC)为美国空军量身定制的效能计算方法[9]，该方法规定系统效能E可以看作是可用性A，可靠性D以及系统能力C的函数：

E=A·D·C.

(1)

由于该方法透明性好，便于计算与理解等的特点，因此本文选取ADC法作为后续分析和评估的依据。

1.1.1 可用性A

可用性是对装备工作时间进行描述的特征参数，根据实际情况的不同有着不同的度量方式。使用可用性Ao对固有可用性和可达可用性进行了综合考虑，可以较好地反映航空装备在实际使用条件下的可用程度，故文中选用，其表达式如下：

(2)

式中：TBF为平均故障间隔时间；TTR为平均修复性维修时间；TMD为平均延误时间。

1.1.2 可靠性D

可信度是某一时间间隔内，任务成功的条件概率矩阵，即

(3)

式中：dij表示任务开始时装备处于i状态，经过预期任务时间装备处于j状态的概率，i,j=1,2,…,n.

由于航空装备任务期间一般是无法维修的，即任务维修度为0. 因此可认为此时可信度就是任务可靠性，即

(4)

式中：t为本次任务执行时间。

1.1.3 系统能力C

系统能力是装备在给定的条件下，达成任务目标的概率矩阵，即

C=[c1,c2,…,ci,…,cn]T，

(5)

式中：ci表示装备处于i状态时达成任务目标的概率。

现代化的空中作战是敌我双方在各自地面指挥所、空中预警指挥部、电子信息干扰机等模块所提供的信息和火力支援下，由多机群联合开展的作战行动[10]。本文研究对象以航空兵部队中歼击机、歼击轰炸机、歼击直升机等攻击型装备为主，所承担任务主要包括拦截敌空中飞行目标、保卫地面(海面)目标、与敌升空拦截我方的歼击机进行空战、掩护对地攻击飞机的突防等。构建的效能评估指标体系以装备的机动性、杀伤性、电磁对抗性等攻击性指标为主。

纵观当前空战模式，主要以超视距和视距内作为主流作战划分阶段。作战过程变化催生了体系对抗强度增大、空战节奏加快、机动性需求俱增、电磁对抗程度趋于白热化等特点[11]。基于此，本文将空战装备效能指标体系细化为超视距打击能力和视距内作战能力。

超视距打击能力应具备以下4点特征：

1)空- 空导弹具备一定的超视距杀伤力；

2)机载雷达应具备一定的电子对抗性；

3)载机信息系统应具备从外部获得信息支援的能力；

4)载机具备良好的隐身性。

视距内作战能力具备以下3点特征：

1)近距武器具备较强的杀伤力，能够达到快速瞄准的目的；

2)载机具备一定的抗击打能力；

3)作战飞机具备较为优秀的机动性，可在极限状态下摆脱敌方。

综上所述，本文所构建的空战装备效能指标体系如图1所示。

1.2 空战装备体系能力指标项计算

结合战场环境仿真与信息化空中对抗体系的仿真模型与武器装备的试验数据，共提取得到10 000组数据(图1中的最底层战术技术指标数据)。通过不同方法定量计算(评估)得出超视距杀伤力、电子对抗能力、态势感知能力、隐身性、近距离火力参数、生存性和敏捷性共7项指标能力的结果，限于篇幅原因，在此以超视距打击能力为例对文中计算(评估)过程进行说明。

超视距状态下的空战装备以中远距离空- 空导弹为主，需要在导弹动力装置、制导系统和战斗部的共同作用下达到毁伤效果。由于中远程导弹主要遵循“先敌发现，先敌打击”的攻击原则，在普通空- 空导弹的火力计算模型基础上，本文还对导弹的最大实际射程和导弹制导类型进行了考虑，计算公式如(6)式所示。

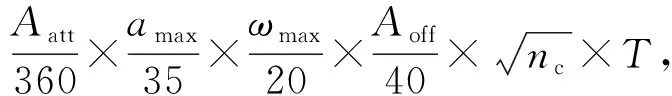
(6)

式中：nm为同类中远程导弹挂点数量；ΔH为允许发射的总高度差；Ps为单发弹杀伤概率；Aatt为发射包线总攻击角；amax为导弹最大过载；ωmax为导弹最大跟踪角速度；Aoff为超前及滞后离轴角之和；nc为同类导弹挂载数量；T为导弹制导的可操作程度，导弹制导类型按照操纵类型可分为主动和半主动两类，主动弹T取1.2～1.5，半主动弹T=1.0.

由于空战装备的效能评估工作是对底层指标的综合评估，图1中第3层的指标能力评估(计算)结果，均可由最底层指标通过不同方法定量得出，在此不再赘述。同时，为确保各底层指标项在单位和采样上的差别不会对信息在转移和汇聚过程中造成影响，本文计算(评估)所得的效能指标能力值均为标量，以此最大限度保证所得结果不会受到由于数据单位和评估方式的不同对信息造成的严重损失，同时也为后续神经网络模型的输入端口统一了标准，降低了由于聚合方法不同导致聚合结果的差异，进而影响神经网络模型的训练效果。表1及表2给出了部分样本数据集。

1.3 基于Elman神经网络的效能边缘分布预测结果

人工Elman神经网络作为一种典型的局部回归网络模型，它在逆向传播(BP)人工神经网络基本结构的基础上，通过存储内部状态具备了映射动态特征的功能，从而使系统具有一定的变特性能力[12]。其主要结构包括输入层、结构层、隐含层和输出层。隐含层的作用是反馈连接层神经元信号并接受输入层神经元的输入，结构层则可以储存之前隐含层神经元的输出[13]。与其他人工神经网络相比，Elman神经网络以结构层为基础形成的局部反馈效果可以记忆过去的状态，并在下一时刻与输入层一同作为隐含层的输入，因此对于动态非线性系统具有较强的适应性。此外，Elman神经网络的反馈机制使得较少的系统输入对预测结果影响并不明显，每一层的输入为上层节点的加权和，因此可以减少网络输入层的单元数，其结构如图2所示，其中：k为神经网络的迭代次数，k=1,2,3,…,K；y(k)为输出层m维的输出向量；x(k)为n维中间层节点的单元向量；u(k)为r维输入向量；ω1、ω2、ω3则分别为结构层与隐含层，输入层与隐含层、隐含层与输出层之间的连接权值矩阵。预测流程步骤如图3所示。

图1 空战装备效能评估指标体系Fig.1 Effectiveness evaluation index system of air combat equipment

表1 超视距样本数据集

表2 目视内样本数据集Tab.2 Visual sample data set

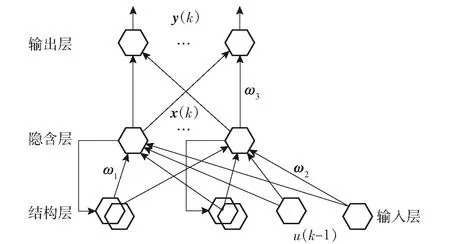
图2 Elman神经网络结构图Fig.2 Structural chart of Elman neural network

图3 Elman神经网络预测步骤图Fig.3 Flow chart of Elman neural network prediction

Elman神经网络的非线性状态空间表达式如(7)式所示：

(7)

式中：xc为n维反馈状态向量；g(*)为输出层神经元的传递函数，可看作是隐含层的线性组合输出；f(*)为神经元的传递函数。权值的修正采用BP算法进行，学习指标采用的误差平方和函数如(8)式所示：

(8)

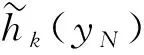
对表1和表2中数据进行归一化处理后，以前2 000组数据作为超视距打击能力和视距内作战能力的神经网络训练数据，其中超视距打击能力的输入端为4，输出端为1；视距内作战能力的输入端为3，输出端为1；通过设定隐含层神经元个数、训练函数以及指定延迟，得出二者的Elman神经网络训练模型。需要说明的是，由于底层指标采样结果单位不同的原因，难以将底层指标直接作为神经网络的输入项，故未选用其作为网络的输入项指标进行训练，而是通过计算(评估)后将结果转化为标量。以该模型对余下8 000组数据进行预测分析，分别得到了超视距打击能力R及目视内作战能力S的模型预测值(下文简称R值和S值)，选取部分如表3所示。以二者预测结果为基础，结合任务过程中装备的可靠性和可用性，计算得出的该型武器装备超视距和视距内的系统效能值，数据散点图如图4所示。

图4 超视距- 目视内模型预测值散点图Fig.4 Predictive scatter plots of over horizon-intra visual model

观察散点图数据分布，发现R值与S值呈现出一定的正相关性，这种非线性变量间的相关程度，通常可由Kendall秩相关系数τ进行描述[14]。表3中第4列列出了以Kendall秩相关系数对“R”、“S”二者预测值之间的相关系数评价，计算公式如(9)式所示：

τ=P[(X1-X2)(Y1-Y2)<0]-
P[(X1-X2)(Y1-Y2)>0]，

(9)

式中：(X1,Y1)和(X2,Y2)为分别为独立同分布的随机变量，P[(X1-X2)(Y1-Y2)>0]为X和Y相一致的概率，说明X和Y的单调性相同；P[(X1-X2)(Y1-Y2)<0]为X和Y不一致的概率，说明了X和Y的单调性反向。Kendall秩相关系数τ不随X和Y的边缘分布单调性的变化而变化。

表3 部分预测值及其相关系数Tab.3 Partial predicted values and correlation coefficients

当τ>0时，X1和X2呈正相关；当τ<0时，X1和X2呈负相关；当τ=0时，X1和X2的相关性不能确定，需要借助其他方法判断。通过观察表3中的相关系数τ，发现R值和S值之间存在明显的正相关性，忽略这种相关性将使得所构建的评估模型精度大幅降低，难以推广使用。

2 Copula函数模型的择优

通过上文所述，由于R值和S值之间具有的相关性结构，使得一维模型的整体构建方式并不能照搬到多元情形中去，主要原因是多维变量的联合分布除了与边缘分布有关之外，更重要的是与变量间相关性密切相关。对多变量联合分布模型进行建模的最关键步骤就是构造变量间的相关性结构，如近些年比较流行的支持向量机模型，其实质就是构造二维变量相关性的核函数，本文选用的Copula函数亦是采用同样的思维方式。在判断出变量之间明显的相关性后，本文采用Copula函数模型的主要建模分析步骤如下及图5所示，图5中，A-D法为Anderson-Dareling检验法，Q-Q图检验法为Quantiles-Quantiles检验法。

步骤1对数据模型间的相关性进行计算；

步骤2判断边缘分布类型；

步骤3列举适当的Copula函数备选；

步骤4对Copula函数进行未知参数估计；

步骤5对Copula函数模型进行拟合优度检验；

步骤6绘制变量的联合分布模型；

步骤7结合优度检验结果和数据分布情况，选取最优Copula函数模型。

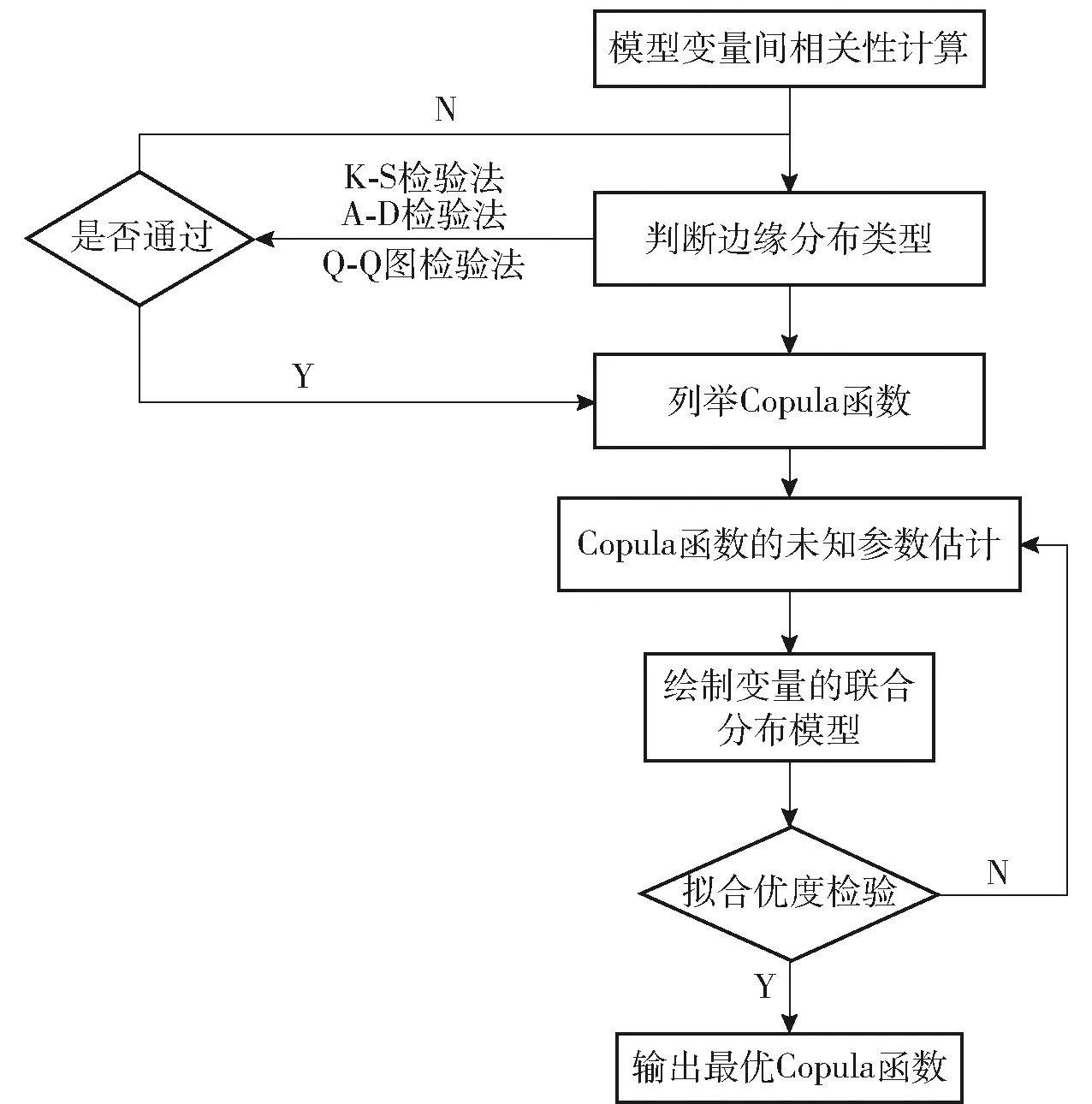
图5 Copula函数模型的择优步骤图Fig.5 Construction flow chart of Copula function model

2.1 二元Copula函数模型

Copula函数作为一种分析函数相关性并进行多元统计的处理方法，可以看作是一种连接一元边缘分布和其多元联合分布的特殊函数。

依据Sklar定理[15]可知，若F为具有连续边缘分布F1(x1),F2(x2),…,FN(xN)的联合概率分布函数，则存在一个唯一的Copula函数C，满足

F(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN))，

(10)

式中：C为与F1(x1),F2(x2),…,FN(xN)对应的Copula函数。同理，通过Copula函数C的概率密度函数c和边缘分布F1(x1),F2(x2),…,FN(xN)可以求出N元分布函数F(x1,x2,…,xN)的概率密度函数：

(11)

式中:f(x1,x2,…,xN)是边缘分布F1(x1),F2(x2),…,FN(xN)的概率密度函数。通过(10)式，Copula函数可以在不对各变量边缘分布加以限制条件下求得变量的多维联合分布，且对非线性、非对称性的变量预测具有良好适应性，使得构建多维概率模型的建模与相关性分析可以分开进行，建模难度大大降低。

2.2 边缘分布类型的判断

首先筛选5种具有代表性的一维分布类，分别为标准正态分布、指数分布、对数正态分布、威布尔分布和伽马分布。以上文的Elman神经网络效能预测结果，采用A-D检验法与Q-Q图检验法相结合的方法对上述5种待选分布类型的形状参数、尺度参数和位置参数进行拟合[16]，判断边缘分布类型。

A-D检验法的计算公式如(12)式所示。

(12)

式中：K为样本数量；GK(x)为经验频率分布；G(x)为待验函数的分布形式；ω(x)为权重函数，计算公式为

ω(x)=[G(x)(1-G(x))]-1.

(13)

A-D检验法拟合结果的优度检验值如表4、表5所示，表中P值为当原假设为真时所得到的样本观察结果或更极端结果出现的概率：P值越大表示拟合程度越高；当P值越小，拒绝原假设的理由越充分，即说明该种分布越不适于拟合样本的数据。

表4 超视距样本拟合优度检验值Tab.4 Goodness of fit test value R

表5 目视内样本拟合优度检验值Tab.5 Goodness of fit test value S

由于标准正态分布与威布尔分布的A-D检验值均高于其他分布，通过Q-Q图继续对比仿真数据和待选分布的拟合度。理论上，当二者的分位数分布大致相似时，Q-Q图应为一条直线，反之当仿真数据分位数与中心线偏离较大时，则表明所选分布与仿真数据并不匹配。图6和图7中：威布尔分布的比例参数为1.3，形状参数为5.2；威布尔分布相比于标准正态分布而言，对于与仿真数据的分位数拟合度更胜一筹，亦表明二者有着近似相同的分布类型。

图6 超视距打击能力与威布尔分布、标准正态分布 的Q-Q检验拟合图Fig.6 Q-Q fitting test chart of R and Weibull distribution and normal distribution

图7 目视内作战能力与威布尔分布、标准正态分布 的Q-Q检验拟合图Fig.7 Q-Q fitting test chart of S and Weibull distribution and normal distribution

为保证所选边缘分布类型的正确性，继续做出样本分布的概率密度图，同时画出威布尔分布、对数正态分布、指数分布3种分布的概率密度曲线，拟合结果如图8和图9所示。通过图8和图9观察发现威布尔分布对二者的拟合结果最为准确，这也验证了Q-Q图和A-D检验法结论的正确性。

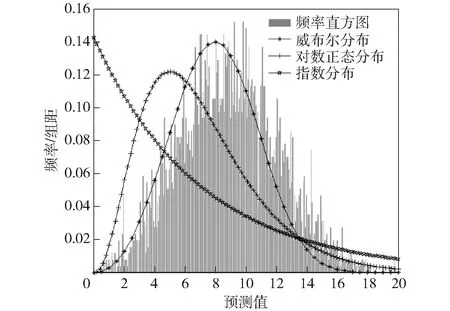
图8 3种分布样式在超视距的概率密度拟合图Fig.8 Fitting map of probability densities for three distribution patterns and value R

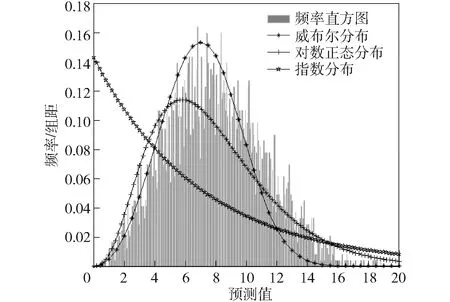
图9 3种分布样式在目视内的概率密度拟合图Fig.9 Fitting map of probability densities for three distribution patterns and value S

综上所述，可以得出空战装备效能指标体系中的二级子式均符合威布尔分布的结论。

2.3 Copula函数模型的择优

针对2.2节判断所得的边缘分布类型，选取5类常见Archimedean Copula函数，分别为Gumbel Copula函数、Clayton Copula函数、T-Copula函数、Frank Copula函数和Joe Copula函数，具体见表6.

5种Copula函数模型中，选取基于最大似然函数的AIC准则、贝叶斯信息BIC准则、χ2检验以及K-S检验4种方法对函数进行拟合优度检验[17]，具体结果见表7.

4种判别准则中，AIC和BIC准则的判别原理基本相似，均是利用Copula函数的似然函数作为判断拟合效果优劣的依据，待判定Copula函数的AIC值和BIC值越小，就越符合原始样本数据。

表6 本文所用到的Archimedean Copula函数Tab.6 Archimedean Copula function used in the present paper

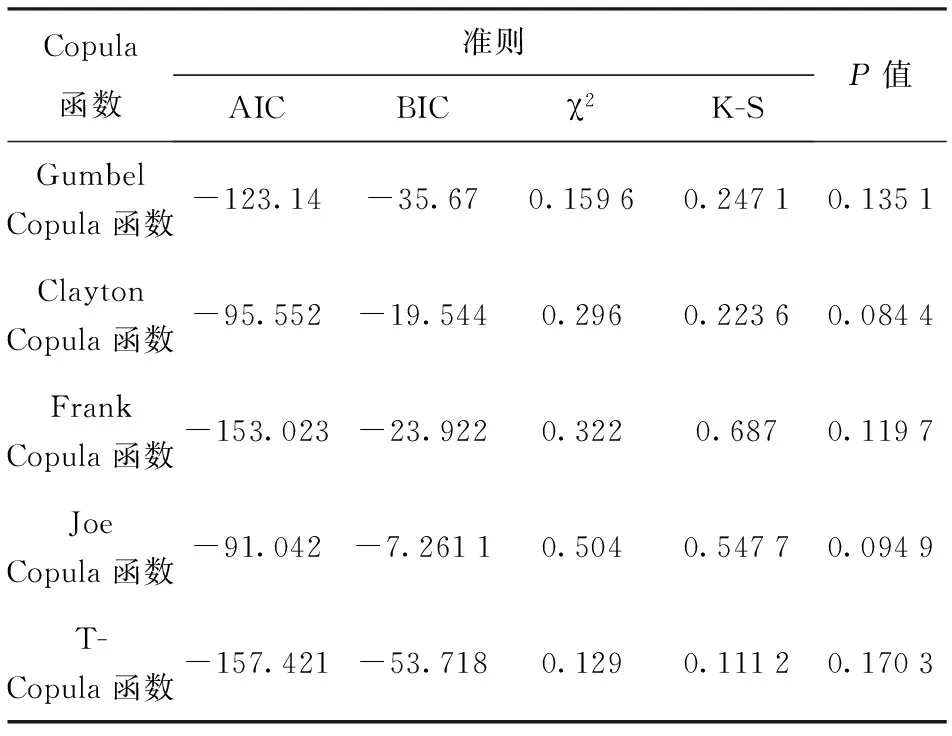
表7 不同Copula模型的拟合优度检验Tab.7 Goodness of fittest values of different Copulafunctions

假设(x1,y1),…,(xK,yK)是极值样本，F1和F2是边缘分布函数，记ui=F1(xi)，vi=F2(yi)，i=1,…,K. AIC和BIC公式如(14)式和(15)式所示，待测Copula函数如(10)式所示，其中kC表示Copula模型中未知参数的数目。

(14)

(15)

(16)

式中：p为概率。

χ2检验法的公式为

(17)

式中：Oi表示极值样本点xi的观测累积概率；Ei是由具体分布函数求出的xi的期望累计概率，极值样本点按照升序排列x1

K-S检验法的基本思路是通过计算比较极值样本点的经验概率与理论概率的差值来判断拟合优度[18]，统计量公式为

(18)

式中：DK为Kolmogorov统计量[19]。根据所提取的数据样本，求得取值范围内的HK(x)与H0(x)，而后计算统计量DK，并以样本容量K和显著性水平α，查询DK(α)；通过对比二者之间的关系，即可得出对原假设接受或拒绝的结论。

表7中，5种Copula函数模型的K-S检验P值均大于0.05，表明在95%置信水平下，5种模型均能满足要求。继续观察，发现T-Copula函数模型的AIC准则、BIC规则最小，由于这两种准则的判别原理是以Copula函数的似然函数为优劣依据，因而其值越小，表明模型越符合原始样本数据，拟合精度越高。而T-Copula函数的χ2值和K-S检验值最小也同样印证了相比于其他Copula模型,T-Copula模型对变量分布的描述精度最高。

3 空战装备效能的多维联合分布模型

3.1 基于Copula函数的空战装备效能联合分布

通过观察，表6中所列Copula函数均含有未知参数θ，在构建基于Copula函数的联合分布模型前，务必对未知参数θ值进行估计。本文采用极大似然估计(MLE)方法[20]对参数θ进行估计，MLE可根据分布函数的概率密度导数构建对数似然函数，如(19)式所示，而后通过求解对数似然函数的最值来计算未知参数的估计值。为进一步对2.3节结论进行验证，表8中列出了上述5种Copula函数对参数θ的拟合结果。

(19)

图10 5种Copula函数的效能体系分布图及T-Copula函数的等高线图Fig.10 Five copula function probability density maps and T-Copula function contour maps

基于表8中对参数θ的估值，做出了基于5种Copula函数的空战装备效能联合分布图，如图11(a)～图11(e)所示。其中U和V分别是超视距打击能力和目视内作战能力预测值，Z是所需预测的装备效能的联合预测值。

表8 5种Copula函数的参数θ估计值Tab.8 Parameter θ estimates of five Copula functions

图10中，T-Copula函数所具备的厚尾特性使得其能够较好捕捉到二者在尾部的相关性关系，等高线图10(f)中的数字表示该点装备效能的联合预测值，由于等高线同线等高的特点，其疏密程度反映了坡度的陡缓情况，亦与图10(e)以及图4中散点图的数据分散情况相一致。其余4种Copula函数中：Gumbel Copula函数对左右数据尾部特征的描述能力并不一致，右侧数据的描述能力明显优于左侧，这与图4中散点图的数据分布相悖；Clayton Copula函数反映左侧尾部数据特征描述效果较好，但对右侧尾部数据特征却几乎不具备描述能力；Joe Copula函数对右尾数据特征描述较好，但几乎没有对左尾数据的描述能力；Frank Copula函数具备对中心分布数据的描述能力，但由于其尾部相关系数为0，更加适合尾部相关性为0的数据，故与本文数据特征不符，均排除。

综上所述，T-Copula函数模型能够较为准确的描述变量间相关性特征，基于此所构建的效能分布图与表7中拟合优度检验结果相吻合，与图4中散点图数据分布相一致，故可得出选择T-Copula函数模型作为空战装备效能预测分布的描述模型较为合理的结论。

3.2 联合分布模型的指标评估

联合分布模型的优劣评价指标通常包括预测的准确度、锐度等。为验证模型的准确性，采用概率统计中常用的Q-S方法[21]和Central CPI指标[22]对模型进行评价。评价维度主要包括预测的校准性(用来评价预测分布的形状与实际概率分布的近似程度)、锐度(用来评价预测概率的集中分布程度)等，原理大致如下。

3.2.1 Q-S方法

通过目标联合概率分布划分为99个分位点并计算得出该点的预测值和实际值，可以得出该方法的关键指标Q(wi,zi)，它表示了模型预测值与实际值间的误差，具体表达式为

(20)

式中：wi(i=1，2，3,…,99)为第i个分位点的实际值；zi为该对应点的理论值。

当预测的区间中未能包含理论值zi时，分位点的实际值wi与理论值zi差距也会增大，评价指标Q(wi,zi)会随之升高。当实际值wi的置信区间过大时，虽然能将实际值包含在内，但由于在区间内大多数实际值wi和理论值zi都会有一定距离，因此评价指标Q(wi,zi)也会升高。

综上所述，Q(wi,zi)的值越小说明预测值和实际值越近，预测精度越高。

3.2.2 CPI指标

指标连续分级概率评分可用于检验连续变量概率预测中的连续性，具体定义如下：

(21)

式中：H(F,zi)的值越小，预测结果越精确。

表9中将本文所提方法与经验分布法、参数估计法等传统预测方法以及效能评估中所常用的SEA计算法进行对比验证，运用Q-S方法和CPI指标对4种方法进行评估。其中SEA方法是美国麻省理工学院信息与决策系统实验室所提出的一种系统效能分析方法。该方法的核心思想是通过确定两个系统的属性空间，其中一个是原始参数映射的属性空间，另一个是由原始参数映射的属性空间。对系统能力和使命要求在相同的使命空间进行相互比较，由此计算出系统的效能值。表10展示了4种不同方法在85%和95%置信水平下的置信区间。

表9 概率预测评估结果Tab.9 Evaluated results of probability prediction

表10 预测区间平均宽度Tab.10 Average width of prediction intervals

3.3 指标评估结果分析

观察表9发现，无论是采用Q-S方法还是CPI指标，本文所提方法在4种方法中评价值均为最小值，即预测精度最高。而观察表10，本文方法在85%及95%置信区间下的宽度均为最窄，同样优于其他预测方法。综上所述，可得出本文所提方法所构建的空战装备效能预测模型精度高于其他方法的结论。

4 结论

本文针对传统装备效能评估模型对多维变量间相关性构造困难、联合分布对边缘分布限制过多、非线性数据拟合能力弱等问题进行研究分析，充分利用神经网络模型对非线性数据的良好拟合性以及统计学中常用Copula函数对变量间耦合性描述的优势，较为准确地构造了多维装备效能评估模型，并通过统计学中Q-S值和CPI值对模型精度进行检验，得出以下结论：

1)综合考虑效能评估指标体系的多方面因素，对现有空战武器装备的评估指标进行筛选，凸显现代化的空中作战特点，构建了分层级的空战装备效能指标体系，对效能评估领域的其他工作具有一定借鉴意义。

2)针对信息化条件下空战过程中的不确定性和非线性特点，引入对非线性数据预测具有良好效果的Elman神经网络模型，同时利用其动态反馈机制，构建了在较少的系统输入状态下能够有效工作的4层Elman神经网络模型，对非线性数据的预测评估工作具有一定促进作用。

3)针对传统分析方法中对二维变量相关性描述不足且困难的问题，将统计学中常用的Copula函数引入武器装备的效能评估中，利用其在构建联合分布模型时无需限定边缘分布类型这一特点，较为便捷地构造了效能指标间的相关性结构。

4)将传统神经网络方法与多元Copula函数相结合，提出了一种具有较强适应性和较高精度的武器装备效能联合分布模型构造方法，通过对比模型概率图与仿真数据的散点图，二者分布基本相似，验证了模型的合理性。

5)采用概率预测中常用的Q-S方法和CPI指标对模型的优劣进行评估，并以经验分布、参数估计正态分布和效能评估中常用的SEA方法等4种方法作为对照组。通过计算，本文所用方法的Q(wi,zi)值和H(FC,zi)值均低于传统预测方法，而在同等置信水平的前提下本文方法的平均置信区间为4种方法中最窄，说明本文方法在精度上均优于传统预测方法。

下一步的研究工作将进一步完善指标体系的规模，扩大数据获取渠道。并在此基础上，适度增加Copula函数的选择范围，构建更加完善的评估模型。