基于拓扑势的作战体系网络节点重要度评估方法

王超，郭基联，符凌云

(空军工程大学 航空工程学院，陕西 西安 710038)

0 引言

近年来，随着复杂网络理论研究不断深入，其在基础设施[1]、交通网络[2]、生物医疗[3]、社会结构[4]等工程领域的应用不断增多，其中复杂网络系统结构关系[5]是人们关注的热点。在军事作战体系中引入复杂网络理论可以有效展示出体系作战实体的结构、功能、行为和交互过程，对现实世界实体事件、行为和过程进行具体和抽象描述，为战争行动体系构建和指挥控制提供参考。

体系作战是指由一个或多个兵种的多型装备作战力量在统一部署指挥下，为完成作战任务而实施的复杂联合作战[6]。体系作战联合情报通信、预警指挥、支援保障和作战打击等多种不同功能装备，在统一决策部署下进行。作战体系网络中担任不同角色、具有不同能力属性的装备，在体系中的关键程度有所不同。装备重要度能够折射出其在作战体系网络中的关键程度，可为装备管理优先级评估提供重要依据。

利用图论[7]这一基础工具，各领域学者提出许多基于不同指标的网络节点重要度评估方法[8-11]。以下列举出评估复杂网络中节点重要度的4条常用基本规则。

规则1在复杂网络中，与节点a相连的边的个数称为节点a的度(Degree)，节点的度是描述节点重要性的重要概念，节点度越大，表明该节点与其他节点交互越紧密，重要性越明显[12]。记节点a的度为DE(a)，即

DE(a)=∑δ(i,a)，

(1)

这种评估规则具有较大的片面性，某些重要的核心节点可能度数较小，例如对连接两个网络团的桥节点而言，其度数往往不大，但其对于网络整体结构却十分重要。

规则2文献[13]中提出介数(Betweenness Centraly)判断准则，指出网络中两两节点间经过节点a的最短路径越多，节点a越重要，记节点a的介数为BE(a)，即

(2)

式中：B(i,j)为节点i和节点j之间的最短路径数；B(i,a,j)为节点i和节点j之间的最短路径中经过节点a的数目。

计算节点介数的过程非常复杂，且单一介数指标无法全面描述节点对网络整体结构的重要度。

规则3一个节点越接近网络的中心，它就越重要[14]。表示节点中心性的接近度(Closeness)是一个合适的度量指标，若节点a的接近度大于节点b，则节点a比节点b重要。记节点a的接近度为CL(a)，则

(3)

式中：V为复杂网络中的节点集；vj为V中节点；dij为节点i和节点j之间的最短路径长度。

规则4若一个节点拥有更大影响力的邻居节点，则该节点更重要[15]。即若节点a的邻居节点影响力大于节点b的邻居节点，则节点a比节点b重要。可采用邻居节点的拓展度函数——邻居指数(Neighbor Index)来度量节点的重要性。记节点a的邻居指数为NE(a)，则

(4)

式中：Nb(a)为节点a的直接邻居节点集，即与节点a有且仅有一跳的节点集合；nk为邻居节点影响力裁定系数，nk越大，度数较大的邻居节点对节点a所起的影响作用越强。

基于上述规则，根据如下关系进行重要度排序：

规则1：DE(a)≥DE(b)⟹a≥b；

规则2：BE(a)≥BE(b)⟹a≥b；

规则3：CL(a)≥CL(b)⟹a≥b；

规则4：NE(a)≥NE(b)⟹a≥b.

以上评估方法采用不同方式融合个体与网络结构的关系，采用度、介数、接近度、邻居指数等指标评估节点相对于网络整体结构的重要度。但由于以上4种方法采取单一评估指标，局限性较强，无法综合全面反映出作战网络节点间的拓扑结构演化行为。随着网络科学的发展，有主体行为能力的个体之间依托通信和交互所形成的复杂网络演化行为越来越受到关注[16]。

深入分析作战体系复杂网络的演化行为与组织原则，需要构建从个体到网络整体结构之间的映射模型，本文结合数学中的拓扑学[17]和物理学中的场论[18]思想，提出基于拓扑势的重要度排序方法。在评估节点重要度的过程中，由于各项规则着眼于不同的评估指标，最终产生的重要度排序亦可能不同。为度量拓扑势排序算法的有效性，本文提出覆盖率计算方法，为复杂网络节点重要度排序算法提供量化评估指标。最后通过一个算例对本文所提方法进行分析验证。

1 基于拓扑势的节点重要度排序

1.1 拓扑理论分析

根据拓扑几何理论[19]，将网络G视为由n个节点及其相互作用组成的抽象系统，节点自身会在网络中形成一个势场，网络中节点对其他节点产生作用的同时也受到其他节点的共同作用。节点间的相互作用通过边来传递，作用效果由节点属性指标及节点间的网络距离决定。

1.2 势场描述

给定网络G=(V,E)，其中，V={v1,…,vn}为节点的非空有限集，E∈V×V为节点偶对或边的集合。

作战体系网络具有任务单元与模块化特性，节点间的相互作用效果具有一定的局域限制。

结合势函数理论，节点vi∈V的拓扑势可表示为

(5)

节点的属性指标mj在现实网络中具有不同的含义，如电力网络中的电站发电能力、物流系统网络中的仓库储备能力等，在作战体系网络中可以视为装备的作战能力指标。若不考虑节点之间的固有属性差异，将网络中的所有节点均视为同质节点，拓扑势公式(5)式可简化表示为

(6)

1.3 运算方法

拓扑势指标可以从整体结构上对网络节点间的相互作用进行描述，能够刻画其在网络结构中的拓扑位置差异和节点自身属性反映出的重要度。基于拓扑势的作战体系网络节点重要度评估算法按如下步骤进行：

1)确定影响因子σ. 引入拓扑势熵H优化σ值：

(7)

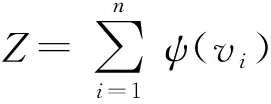
2)将σ优化值代入(6)式，计算作战体系网络中所有节点的拓扑势值。

3)按照拓扑势值大小对节点进行排序，评估节点的重要度。

2 运用覆盖率评估算法性能

网络节点经不同的评估方法进行重要度排序后会生成不同的排序序列。为评价各重要度排序方法所得结果的差异程度，引入覆盖率度量指标。

2.1 覆盖率定义

两个序列间的距离可作为序列相似度的度量指标。将两个序列间存在的一个基础差异看成一个单位距离，进而可以得到序列间的整体距离，即各排序序列相互之间的差异。获得排序序列间的距离后，即可得出不同排序结果的相似度比率。本文采用覆盖率表示序列相似度比率，用相邻元素交换数表示序列间的距离，即需要经过多少次相邻元素的交换操作可使得两个序列排序一致。

定义1邻居交换。给定两个序列a=(a1,a2,…,an)和b=(b1,b2,…,bn)，若∃i∈[1,n]，使得ai=bi+1，bi=ai+1，且∀j∈[1,n]，j≠i∧j≠i+1，aj=bj，则将序列a转换为序列b所需进行的邻居交换次数NS(a,b)记为1，即NS(a,b)=1.

定义2两个序列的距离。给定两个序列a和b，若存在使得k最小的序列集Sk={s1,s2,…,sk},s1,s2,…,sk为满足以下条件的k个序列，即：NS(a,s1)=1，NS(sk,b)=1且∀j∈[1,k-1]，NS(sj,sj+1)=1，NS(sk,b)=1，则NS(a,b)=k+1，即a和b的距离d(a,b)=k+1. 其中，NS(sj,sj+1)表示使sj转化为sj+1需要进行的邻居交换次数。

定义3序列到序列集的距离。给定一个序列a和一个序列集S，则从a到S的距离为

d(a,S)=min {NS(a,i)|i∈S}.

(8)

在重要度排序过程中，可能出现具有等价节点的序列。对于一个给定网络，当排序指标相同时，重要度排序可能不同，将比较序列可能构成的序列集合记为S，将被比较序列可能构成的序列集合记为P，将所有可能序列构成的序列集合记为Q. 进而可将覆盖率表述为

(9)

式中：s表示序列集S中的序列；m、n表示序列集Q中的序列。

2.2 覆盖率数值计算方法

通过计算序列与序列、序列与序列集和序列集与序列集之间的距离，可以得到各个方法排序结果之间覆盖率，即排序的相似度，进而直观反映出各排序方法之间的差异。

1)计算s和P之间的距离d(s,P)。在计算d(s,i),i∈P的过程中，直接计算最小邻居交换数NS(s,i)较为复杂，在此引入一个简单直观方法解决此问题：每个节点有两个属性值，一个是在给定序列s中的序号，一个是在比较序列i中的序号，因此可得到由两个序号集组成的序列x和y，则序列x与y的最小邻居交换次数NS(x,y)即是序列s与序列i的距离d(s,i)。

2)计算全部序列最大的可能距离dmax最直接的方式是构造所有可能序列后，计算最大邻居交换数，此过程存在一个简单方法：假设节点被分割成NE个重要度等级并记为E1，E2，…，ENE，各重要度等级的大小为|E1|,|E2|,…,|ENE|。将序列中元素个数记为N，则任意序列间的最大距离是N(N-1)，每个重要度等级Ei将导致|Ei|(|Ei|-1)个减除，于是有

(10)

3 仿真示例分析

3.1 作战想定

通过结合体系作战相关理论[20-21]与作战实例研究，给出一个空战网络体系作战想定设计，建立指挥体系模型，如图1所示。

图1 指挥控制体系模型图Fig.1 Model of command and control system

以作战指挥部(节点1)为中心，两架预警机(节点2、节点6)为指挥中介，形成作战指挥网络。在指挥网络的控制指挥下，节点2预警机下辖2个战斗机群(节点10～13、节点14～17)，节点6预警机下辖2个战斗机群(节点18～20、节点22～25)，且这两架预警机对每个战斗机群的长机(节点10、节点18、节点14、节点22)直接指挥，战斗机群之间僚机与长机、僚机与僚机之间可相互传递战场信息及指挥指令，由于战斗机装备性能存在差异，指挥体制各有区别。两架预警机(节点2、节点6)分别指挥3架侦察机(节点3～5、节点7～8)，且侦察机信号可与作战指挥部产生交互。地空雷达(节点29)可与预警机(节点2、节点6)、作战指挥部(节点1)、具有先进航电系统的战斗机(节点14)之间进行侦查信息共享。

提取该空中作战体系网络中的装备实体，依据指挥信息传递交互关系对该体系采用复杂网络分析Gephi软件以图论的方式建模，如图2所示。

3.2 常规重要度评估方法排序结果

经过计算，得到基于引言中所列4种常规重要度评估规则的作战网络节点重要度排序。如表1～表4所示。

表1 以度为指标的重要度排序Tab.1 Importance ranking based on degree

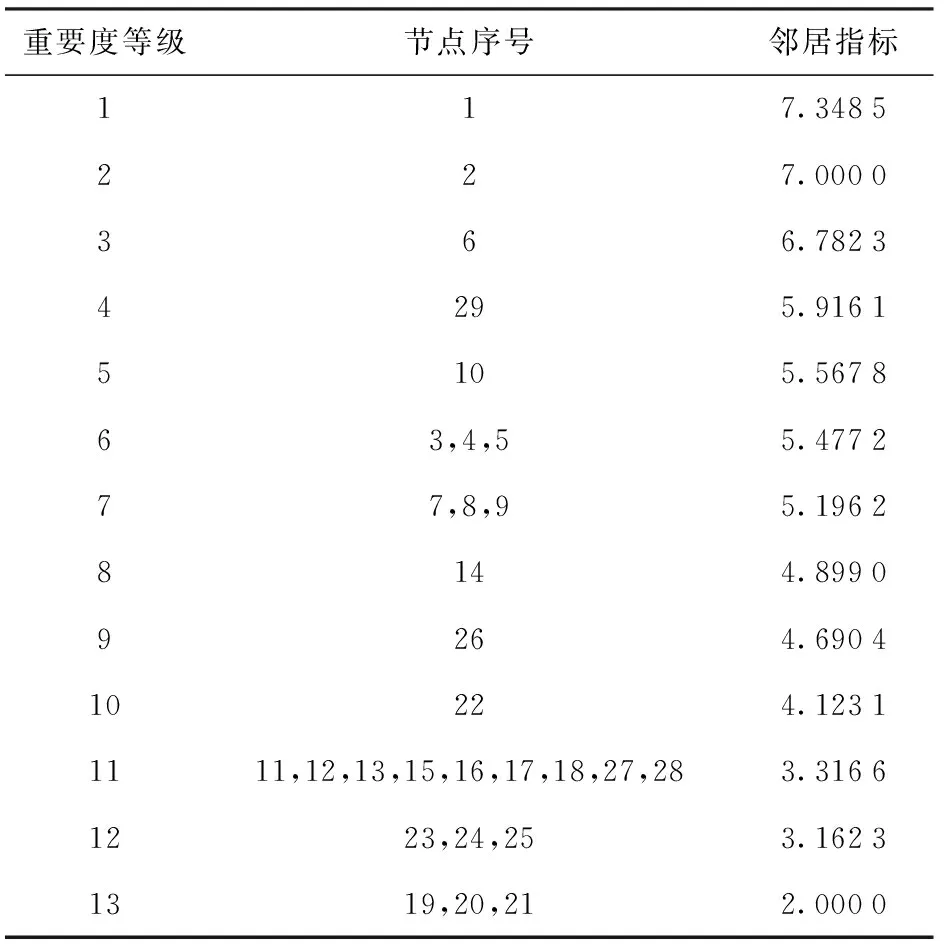
表2 以邻居指数为指标的重要度排序Tab.2 Importance ranking based on neighbor index

表3 以接近度为指标的重要度排序Tab.3 Importance ranking based on closeness

表4 以阶数为指标的重要度排序Tab.4 Importance ranking based on between ness Centrality

从表1～表4的排序结果可以看出，引言中所列4种常规方法可以明确辨别出易于识别的关键装备节点的重要度等级，虽然不同的评价角度相应带来了不尽相同的评估结果，但对关键节点的评估结果较为符合客观实际。而基于度、阶数、接近度和邻居指数的常规重要度排序方法，由于指标选取表征不全面，在对非关键节点的排序中，仍存在重要度等级混淆、多数装备节点重要度无法明确排序的问题。

3.3 覆盖率度量排序方法的性能

针对此作战体系网络，将在不同影响因子σ条件下的拓扑势排序结果分别与度、阶数、接近度和邻居指数的排序结果进行对比，对比结果如图3所示。图3中，Cb表示拓扑势排序对阶数排序的覆盖率，Cd表示拓扑势排序对度排序的覆盖率，Cc表示拓扑势排序对接近度排序的覆盖率，Cn表示拓扑势排序对邻居指数排序的覆盖率。

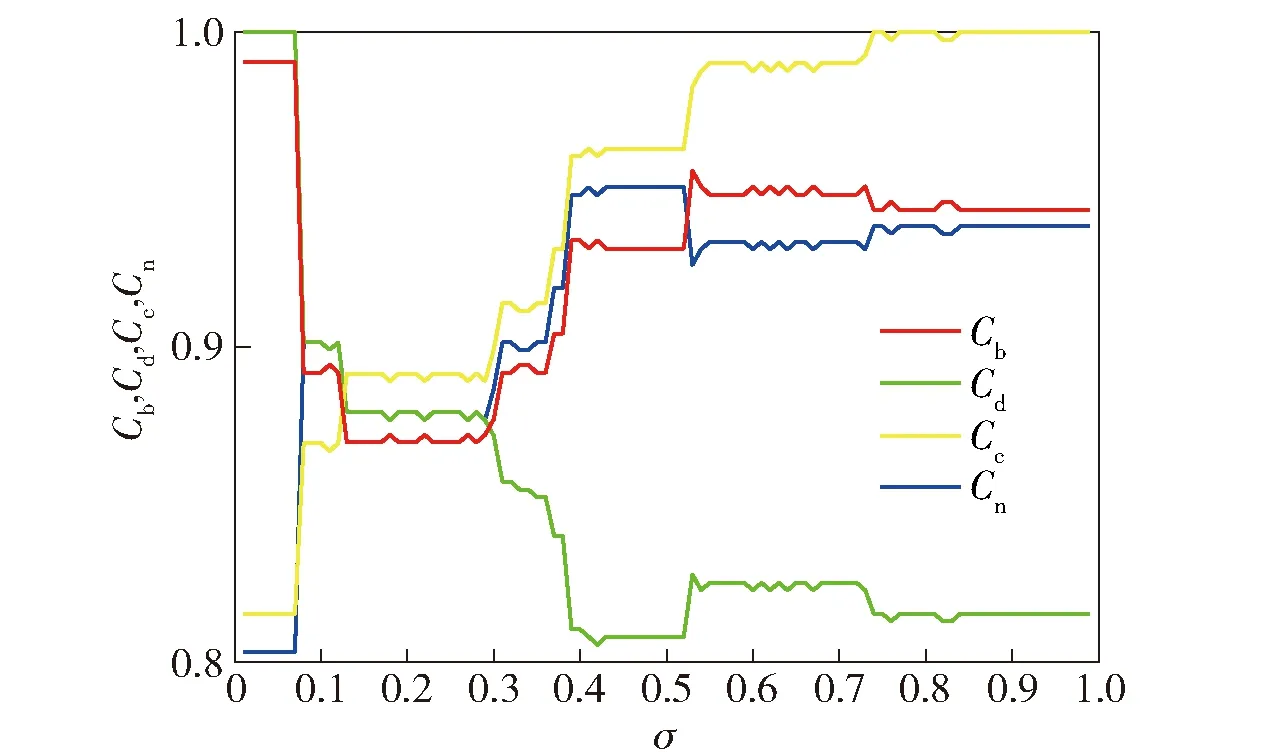
图3 覆盖率随影响因子的变化Fig.3 Change of coverage with impact factors

通过图3可以看出：当0<σ≤0.07时，拓扑势排序算法的排序结果与度排序算法的排序结果完全相同，表明在此范围内，拓扑势排序算法退化为度排序算法，节点的度对重要度排序产生的效应最强；当0.08<σ≤0.29时，拓扑势排序算法的排序结果与度排序算法、介数排序算法、接近度排序算法、邻居指数排序算法的排序结果覆盖率大致相等，表明在此阶段拓扑势排序算法处于这4种算法的均衡状态；当0.29<σ≤0.52时，拓扑势排序算法的排序结果与阶数排序算法、接近度排序算法和邻居指数排序算法的排序结果覆盖率逐渐提高，表明在此过程拓扑势排序算法的排序结果逐渐趋向于这3种算法；当σ≥0.54时，拓扑势排序算法退化为接近度排序算法，节点的接近度对重要度排序产生的效应最强。

由(7)式计算得出此作战体系网络中最优影响因子σ=0.38. 此时，基于拓扑势的作战体系网络节点重要度计算结果如表5所示。

表5 σ=0.38条件下各节点的拓扑势及排序Tab.5 Topological potentials and ranking of nodes forσ=0.38

图4所示为σ=0.38条件下各节点的拓扑势值。从图4中可以看出：节点1作为作战指挥中心，其影响力最大，拓扑势值最高；节点2预警机和节点6预警机作为指挥信息传递的重要中介，重要度排序分别位列第2、3位；各战斗机群长机(节点10、节点14、节点18、节点22)作为骨干火力打击及信息传输共享节点，在作战网络结构中的影响力也较大，拓扑势值高于其余歼击机；节点29地面预警雷达，在体系结构构建及指挥信息传递中发挥重要作用，其拓扑势值也较高；而其余作为非核心节点的作战末端装备，拓扑势值均处在较低水平。从评估结果可以看出，运用拓扑势方法计算的节点势值重要度排序符合客观实际。

图4 σ=0.38条件下各节点的拓扑势值Fig.4 Topological potentials of nodes for σ=0.38

通过(9)式计算可得，当σ=0.38时，拓扑势排序算法的排序结果相对于度、邻居指数、接近度、阶数排序算法的排序结果覆盖率分别为Cd=0.840，Cn=0.902，Cc=0.913，Cb=0.889. 由此可见，基于拓扑势的重要度排序方法以作战体系网络结构中的装备协同作战关系为重心的同时，也较为符合其他常规评估规则。

在基于拓扑势的节点重要度排序算法中，可以结合作战体系网络中不同装备所存在的性能差异，进一步将装备节点的能力指标引入评估过程中，综合分析各装备节点在作战体系网络中的结构以及自身作战能力指标的差异，结合影响作战体系作战能力的各方面因素对装备节点重要度进行评估。

4 结论

本文从节点的重要度概念入手，分析了作战体系网络节点的指挥拓扑结构，提出基于拓扑势的节点重要度测度方法，准确地解决了作战体系网络节点的重要度评估问题。得出主要结论如下：

1)通过示例分析中的评估结果可以看出，运用拓扑势方法计算的作战体系网络节点重要度排序结果符合实际情况，且此方法能够克服常规方法评估指标的片面性，评估结果客观可靠。

2)本文方法将节点拓扑结构影响贯穿于计算过程中，对于不同作战体系网络中的不同装备节点，只需根据其作战能力大小，代入替换不同的节点固有属性值参数即可对网络节点重要度进行评估。

3)基于拓扑势的重要度排序算法与常规重要度排序方法的相似程度较高，排序在综合考虑作战体系网络中装备实体的协同作战关系和装备作战能力的同时，也贴合其他常规评估指标。拓扑势可以自底向上地从网络结构位置和节点属性差异出发，更加全面地评估作战体系网络中装备节点的重要度，能够体现网络的结构特性，相对其他通过片面指标评估节点重要度的方法，此方法更加精确合理。

体系作战是信息化时代背景下的主要作战样式。本文所提方法从装备自身属性能力指标和网络拓扑位置出发评估装备节点在作战体系网络中的重要度，综合分析了不同装备对作战体系网络构建和任务完成能力的支撑效应，能够精确合理地定量计算武器装备对体系作战能力的影响作用，能够更加系统地反映出网络的整体特性，值得在体系作战理论中推广应用。