基于概率假设密度滤波与无迹Kalman滤波的多目标跟踪与识别
2020-09-28邹汝平刘建书
邹汝平,刘建书
(西安现代控制技术研究所, 陕西 西安 710065)
0 引言
现代导弹利用导引头测量信息进行目标检测、跟踪与识别,根据所接收的目标信息进行分析处理以获得所需的目标运动参数(高低角、方位角、径向速度与导弹与目标(简称弹目)相对距离等)[1]。随着导引头技术发展与应用,敌方目标对导引头的欺骗技术也在相应地不断发展,欺骗式干扰目前主要包括:距离欺骗(导引头测量的距离为虚假值,速度为真实值)、速度欺骗(导引头测量的弹目径向速度为虚假值,距离为真实值)以及距离- 速度联合欺骗(距离与速度均为虚假值,但是距离的变化率与测量的径向速度信息呈相关性)[2-3],因此,针对距离- 速度联合欺骗干扰模式下的目标识别面临很大的技术难题。
在抗干扰技术方面,目前已有较多的研究成果。根据目前的研究成果,主要分为两大部分:基于频域、时域、空域及联合域的抗干扰技术;基于目标航迹特性的抗干扰技术。文献[4]提出了基于时空信息处理的目标抗干扰技术。文献[5]详细介绍了一种基于子空间投影的空时自适应处理算法。根据线性代数和三维几何,如果将一个值域空间投影到一个由线性无关向量张成的子空间上,可以抑制垂直于该子空间的数据。在基于子空间的方法中,将接收到的数据投影到与杂波子空间正交的子空间中去除杂波。根据该原理,从而实现了对杂波抑制的抗干扰技术。文献[6]考虑了空间相干有源无源双基地雷达(BSR)在强干扰背景下对非辐射目标观测基线小的特点,根据信号最优检测分辨率统计理论的结论,提出了信息完备性原理。给出了该方法在BSR有源和无源信道间的信息交互组织和目标与干扰器之间的坐标信息获取方面的实际应用。文献[7]分析了各种有源欺骗干扰的基本原理,建立了基于速度- 角度以及距离- 角度的系统跟踪模型,结合无迹Kalman滤波(UKF)算法实现了对目标的抗干扰识别,但是该方法只是针对二维平面模型,未给出在三维空间下的目标识别技术。文献[8]针对距离- 速度联合拖引欺骗干扰下的机动目标跟踪问题,研究了利用接收机自动增益控制电压和目标个数突变信息的干扰判决方式,最后利用UKF实现对目标跟踪。文献[9]根据UKF得到的目标速度、加速度、角加速度、过载等信息进行目标识别,且较好地实现了对干扰目标的识别。
虽然上述文献在抗干扰方面取得了部分研究成果,但是,导引头在进行测量时,回波信息中包含大量的杂波信息,如果在滤波前不进行杂波剔除与点迹航迹关联,则在进行滤波时,在部分点迹航迹关联错误时,滤波器将呈现发散状态,无法实现对干扰目标的识别。
针对上述文献存在的缺陷,本文针对欺骗式干扰中的距离- 速度拖引式干扰,建立了联合拖引干扰及三维目标跟踪模型,通过概率假设密度(PHD)滤波与UKF算法实现对目标跟踪与目标航迹滤波,根据PHD滤波估计的目标位置与速度信息,建立目标航迹,进而根据UKF技术实现对多目标的识别,最后通过仿真实验验证了本文方法的可行性与正确性。
1 距离- 速度联合欺骗干扰模型
针对导引头检测的目标回波信号,距离- 速度联合欺骗干扰模型可用(1)式[7-9]进行表示:
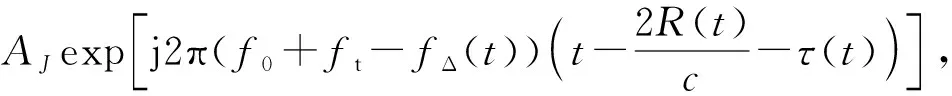
(1)
式中:J(t)为距离- 速度联合欺骗干扰脉冲;t为仿真时间;AJ为干扰脉冲幅值;f0为雷达发射脉冲信号的中心频率;ft为目标脉冲信号的多普勒频移;fΔ(t)为干扰脉冲相对于目标脉冲的多普勒频率偏移量;R(t)为雷达到目标之间的距离;τ(t)为距离拖引引起的时延函数;c为光速。多普勒频移量fΔ(t)和时延函数τ(t)在拖引期必须满足
(2)
(3)
(4)
式中:a为拖引加速度;λ为波长;t1、t2、tJ均为设计参数,满足t1 基于上述距离- 速度联合欺骗干扰原理,图1给出了在拖引加速度为10 m/s2下的目标轨迹。图1中:红色曲线为真实目标轨迹,绿色曲线为距离- 速度在拖引加速度(即(3)式和(4)式中的a)大于0 m/s2时的假目标轨迹(距离- 速度前拖),蓝色曲线为距离- 速度在拖引加速度小于0 m/s2时的假目标轨迹(距离- 速度后拖)。如图1所示,在目标施加拖引干扰后,假目标与真目标的轨迹发生了较大变化,因此,本文针对目标轨迹的空间变化进行目标识别技术研究。 图1 距离- 速度拖引三维目标航迹Fig.1 Range-velocity simultaneous pull-off three-dimensional target track (5) 式中:Fk、Vk、h(·)、Wk+1、Zk+1分别为状态矩阵、过程噪声、测量方程、观测噪声和观测值。其中,Fk的表达式为 (6) 式中:T为采样周期;选取Zk+1=[θ,γ,v,d]为观测量,θ、γ为导引头的框架角,v为弹目径向速度,d为导弹与目标的相对距离。根据导引头的测量原理,可得如下测量方程: (7) 为能有效实现目标识别,把(7)式所示的测量方程写为如下形式(距离滤波与速度滤波): (8) (9) 下面给出本文用到的相关坐标系转换矩阵,导引头坐标系S到天线坐标系A的转换矩阵为 (10) 式中:弹体坐标系P到导引头坐标系S的转换矩阵为 (11) 式中:λ为导引头滚转角。惯性系I到弹体系P的转换矩阵为 (12) 式中:ϑ、ψ、ζ分别为导弹姿态的俯仰角、偏航角和滚转角。上述坐标系的详细定义及转换矩阵请参见文献[10]. 基于PHD滤波的多目标跟踪技术是目前较为成熟的目标跟踪技术。因此,本文在进行目标跟踪时,采用PHD滤波器,同时,通过高斯混合(GM)技术,得到GM-PHD滤波器。基于GM-PHD滤波的多目标跟踪技术[11-13]主要包括如下步骤。 1)目标状态预测。根据k-1时刻导引头的采样值,目标可能的后验目标强度满足(13)式: (13) Dk|k-1(xk|Z1:k-1)=DS,k|k-1(xk|Z1:k-1)+ (14) 式中:DS,k|k-1(·)、Dβ,k|k-1(·)、γk(xk)分别为目标存活强度、衍生目标强度和新生目标强度。 2)目标状态更新。如果k时刻目标状态预测PHD满足下列形式: (15) 则k时刻目标可能的后验PHD也满足下列形式: (16) 式中:pD,k为目标检测概率。 3)相似航迹合并与假目标剔除。随着导引头采样时间的推进,GM-PHD滤波器针对导引头测量数据GM项不断增长。因此,根据相似航迹合并与假目标剔除的思想,删除权重较小的假目标航迹,对相似航迹进行合并。 4)获取目标状态。首先,根据(17)式计算测量数据中可能的目标个数,即 (17) (18) 众所周知,著名的Kalman滤波技术是针对线性系统,而对非线性系统则显得较为乏力。根据前面建立的系统模型可知,本文的滤波模型属于非线性模型,因此,本文将采用UKF实现对系统状态滤波。UKF方法的主要过程[9,14]如下。 1)滤波模型初始化: (19) 式中:x0为初始状态;0为初始状态估计;P0为初始协方差。 2)对于所有的采样时刻k=1, 2,3,…等进行迭代计算。 ①根据Sigma点计算公式,对系统状态量进行UT变换。 ②根据系统模型计算目标轨迹预测值为 χi,k+1|k=f(χi,k), (20) 式中:χi,k为当前时刻状态值;f(·)为目标状态函数;χi,k+1|k为下一时刻的目标状态。基于无损变换(UT)得到目标状态预测值: (21) 式中:ωi为状态权重;n为UT点数。 计算预测方差,得到一步预测方差阵: (22) 通过测量方程对各个sigma点进行测量值计算: i,k+1|k=h(χi,k+1|k), (23) 通过UT的权重系数加权求得预测测量值: (24) ③更新方程。计算理论的信息方差得到 (25) 式中:Pzz,k+1|k为估计的观测值与真实值之间的协方差矩阵;Rk+1为k+1步的滤波方差。 计算协方差得到 (26) 计算UKF增益矩阵得到 (27) 更新误差协方差得到 (28) 更新滤波状态值得到 k+1|k+1=k+1|k+Kk+1[Zk+1-k+1|k]. (29) 以上即为UKF的主要过程。 本文针对目标匀速直线运动与匀速转弯运动(包括匀速直线与匀速转弯两种运动,目标被导引头锁定前为匀速直线运动,目标被锁定后,目标采用匀速转弯运动进行逃逸。本文在进行仿真时,在施加第一次干扰时,目标开始以转弯角频率0.05 rad/s的机动方式进行匀速转弯机动)验证本文方法的有效性,仿真参数同文献[9]所示,具体如下。 1)初始弹目距离为30 km. 2)目标飞行状态:速度为260 m/s、弹道倾角为0°、弹道偏角为170°(向X轴负向飞行,便于目标轨迹观测);导引头初始框架角为30°(高低角)、5°(方位角);目标实施的4次干扰施加时间:开始时间为[9 s;14 s;18 s;23 s],结束时间为[20 s;25 s;30 s;35 s]。 3)噪声方差Q=diag[0.05 m;0.01 m/s;0.000 1°],距离滤波方差σR=diag[152m2;1 m2/s2;0.000 1°;0.000 1°],速度滤波方差σv=diag[52m2;1 m2/s2;0.000 1°;0.000 1°]。 根据上述仿真参数,针对目标作匀速直线运动,目标跟踪结果如图2所示。 图2 多目标跟踪结果Fig.2 Multi-target tracking results 图2为采用5次蒙特卡洛仿真得到的仿真结果。由图2可知,在绝大多数测量时间内,PHD滤波得到的目标个数与真实目标个数相同。通过统计,准确跟踪(PHD滤波识别的目标个数等于真实目标个数)目标的概率为80.23%,目标误识别概率(识别的目标个数大于真实目标个数)为14.2%,目标漏识别的概率(识别的目标个数小于真实目标个数)为5.57%. 从工程可靠性角度分析,目标误识别概率对实际工程具有一定的积极作用,误识别的目标可以通过航迹维持等消除,但是漏识别目标,可能会造成真实目标的丢失。因此,基于PHD滤波的目标可靠识别概率为94.43%,基于PHD滤波的目标跟踪技术能够很好地实现多目标跟踪。 在目标跟踪的基础上,采用本文的目标识别方法实现对真实目标的识别,仿真结果如图3~图5所示。 图3 距离- 速度拖引三维轨迹(目标匀速直线运动)Fig.3 Range-velocity simultaneous pull-off three-dimensional target track (uniform rectilinear motion of target) 图4 距离- 速度拖引速度曲线Fig.4 Range-velocity simultaneous pull-off velocity curves 图5 距离- 速度拖引加速度曲线Fig.5 Range-velocity simultaneous pull-off acceleration curves 图3为目标匀速直线运动时根据PHD滤波跟踪的真实目标与距离- 速度拖引三维航迹(图中红色曲线为真实目标轨迹,蓝色曲线分别为施加的4次拖引轨迹)。由图3可知,目标作匀速直线运动,4次拖引中前拖和后拖各施加了两次。对比滤波结果与真实目标轨迹,PHD滤波的位置均方根误差(RMSE)为11.25 m,速度RMSE为4.57 m/s. 图4为采用UKF航迹滤波的距离- 速度拖引速度曲线,图5为采用UKF航迹滤波的距离- 速度拖引加速度曲线。通过图4与图5可知:针对目标作匀速直线运动,目标在施加距离- 速度拖引后,根据UKF得到的速度与加速度曲线很容易判断真实目标与虚假目标;施加拖引后拖引的速度与加速度均在短时间之内发生了较大改变,速度迅速超出设定的阈值,加速度信息在拖引发生时发生突变,而目标的速度与加速度均能维持在稳定状态。联合速度和加速度信息,在拖引施加1 s之内即可实现对假目标的识别。因此,通过获得的目标速度和加速度信息能够很好地实现对目标的识别。 针对目标作匀速转弯运动,仿真结果如图6~图8所示。 图6 距离- 速度拖引三维轨迹(目标匀速转弯运动)Fig.6 Range-velocity simultaneous pull-off three-dimensional target track (uniform turning motion of target) 图7 距离- 速度拖引速度曲线Fig.7 Range-velocity simultaneous pull-off velocity curves 图8 距离- 速度拖引加速度曲线Fig.8 Range-velocity simultaneous pull-off acceleration curves 图6为目标匀速转弯运动时根据PHD滤波跟踪的真实目标与距离- 速度拖引三维航迹(图中曲线的具体含义同图3,红色曲线为真实目标轨迹,蓝色曲线分别为施加的4次拖引轨迹),对比滤波结果与真实目标轨迹,PHD滤波的位置RMSE为14.25 m,速度RMSE为6.12 m/s. 同时,也可以看出,在目标机动后,PHD滤波的精度有所下降。 图7为采用UKF航迹滤波的距离- 速度拖引速度曲线,图8为采用UKF航迹滤波的距离- 速度拖引加速度曲线。通过图7与图8可知:针对目标做匀速转弯运动,目标在施加距离- 速度拖引后,拖引1、拖引2与拖引3根据速度曲线很容易能够判断出真实目标与假目标,对于拖引4,滤波得到的目标拖引速度与真实目标速度比较接近;但是通过加速度曲线可以看出,拖引4的加速度比真实目标的加速度大很多,即通过加速度曲线能够进一步识别真假目标。联合速度和加速度信息,在拖引施加1.3 s之内即可实现对假目标的识别。因此,在目标作匀速转弯运动时,联合UKF航迹滤波得到的速度与加速度信息,能够完成对多目标的识别。 为有效提高导引头末制导阶段抗干扰技术水平,本文提出了基于PHD滤波的目标跟踪与基于UKF滤波的目标识别方法。根据导引头量测数据,基于PHD滤波实现对多目标跟踪,在此基础上,通过UKF滤波提取目标的速度和加速度信息(利用距离滤波与速度滤波),通过目标速度和加速度信息的变化特征,能够实现对真假目标的识别,仿真结果进一步验证了本文设计方法的有效性和可行性。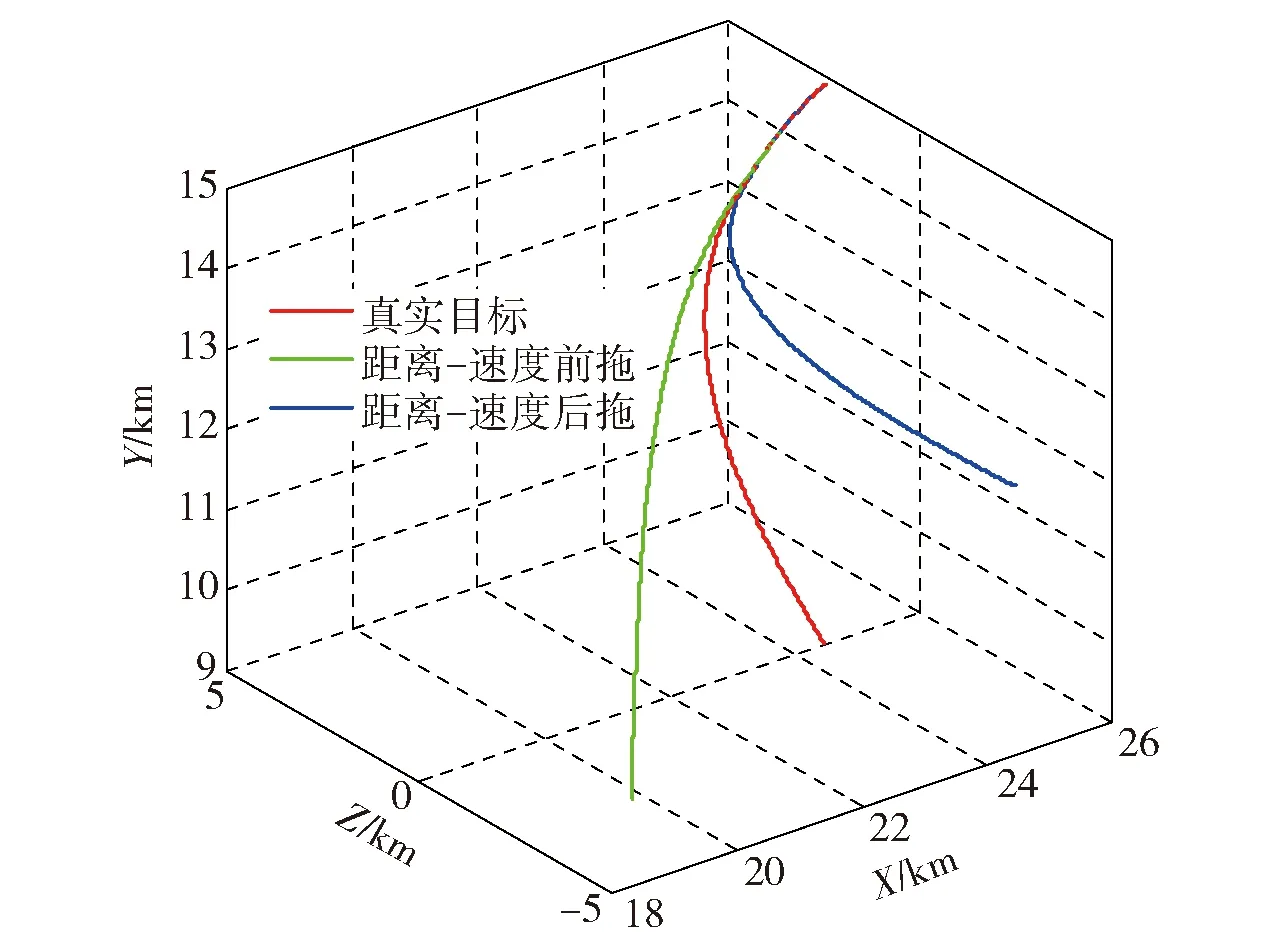
2 系统跟踪模型建立
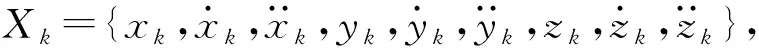
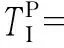
3 基于高斯混合PHD滤波器的目标跟踪


Dβ,k|k-1(xk|Z1:k-1)+γk(xk),

4 UKF主要过程



5 仿真分析







6 结论
