([0,1]，[0,1])-模糊拟阵的基和秩函数

代恩华，修振宇

(1.聊城大学东昌学院数学与信息工程系，山东 聊城 252000;2.成都信息工程大学应用数学学院，四川 成都 610000)

拟阵是图和矩阵的推广，在数学中扮演着重要的角色,尤其是在应用数学中，正是简单有效的贪婪算法所要求的结构[1].1988年,Goetschel等[2]定义了有限集E上的模糊拟阵.Shi[3]提出了L-拟阵，其中L为完全分配格.Huang等[4]证明了完备的[0,1]-拟阵等价于模糊拟阵.在L-拟阵的理论框架下，基、圈、秩函数和闭包算子等概念被广泛研究[5-10].Shi[11]提出一种新的拟阵的模糊方式，即，M-模糊化拟阵，其中M为完全分配格；又定义了M-模糊化秩函数，并证明了M-模糊化秩函数和M-模糊化拟阵是一一对应的.Yao等[12]定义了基映射和圈映射并证明了模糊化拟阵可由这两个映射刻画.关于M-模糊化拟阵的研究，还有很多概念，诸如M-模糊化相关集[13],M-模糊化α-平坦族[14]和M-模糊化闭包算子[13],都可以等价刻画M-模糊化拟阵.

Shi[3]提出了更为宽泛的模糊拟阵，即，(L,M)-模糊拟阵，其中M和L都是完全分配格，这是L-拟阵和M-模糊化拟阵的逻辑推广.有关L-拟阵和M-模糊化拟阵的基和秩函数的研究都取得了不少成果[4,10-12].而目前关于(L,M)-模糊拟阵的研究并不多，这促使我们来探究(L,M)-模糊拟阵中基和秩函数的情况.在本文中，当M和L都取为[0,1]时,给出闭的完备的([0,1],[0,1])-模糊拟阵的概念，并建立相应的基公理和秩函数公理.

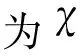
A=B};

A=B}.

定义1[16]设A∈[0,1]E且a∈[0,1].定义模糊集A的截集如下：

A[a]={e∈E:A(e)≥a},A(a)={e∈E:A(e)>a}.

定理1[16]对∀A∈[0,1]E和a∈[0,1],A(a)=∪b∈(a,1]A[b]=∪b∈(a,1]A(b).

定义2[3-4]设A∈[0,1]E，N表示自然数集.称映射|A|:N→[0,1]是A的模糊势，若对∀n∈N,|A|(n)=∨{a∈[0,1] : |A[a]|≥n}.

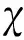
定义4[11]称逆序映射λ:N→[0,1]是一个模糊自然数，若它满足λ(0)=1,∧n∈Nλ(n)=0.所有的模糊自然数记为N([0,1]).

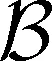
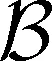
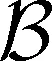
(i) 对∀A∈[0,1]E,0≤R(A)≤|A|;

(ii) 若A,B∈[0,1]E和A≤B，则R(A)≤R(B);

(iii) 对∀A,B∈[0,1]E,R(A)+R(B)≥R(A∧B)+R(A∨B);

(iv) 对∀a∈(0,1]和A∈[0,1]E，R(a∧A[a])[a]=R(A)[a].

1 模糊基的模糊族

借助定理3和分层思想，可以将[0,1]-拟阵中的模糊基族推广如下：

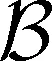
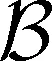
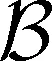
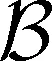
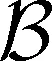
a}.

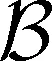
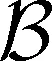
证明由定理7,8和定理1可得，

根据定理8和9,可得下面的结论：

定理10模糊基的模糊族和闭的完备的([0,1],[0,1])-模糊拟阵是一一对应的.

2 模糊秩函数

如定理5，闭的完备的[0,1]-拟阵可由[0,1]-模糊秩函数等价刻画.本节将给出闭的完备的模糊拟阵的秩函数公理.基于定理5和分层思想,可以推广[0,1]-模糊秩函数如下：

证明由定理11,12和定理1可得，

根据定理12和13,可得下面的结论：

定理14模糊秩函数和闭的完备的([0,1],[0,1])-模糊拟阵是一一对应的.