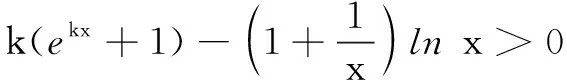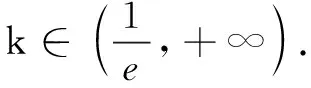同构法求参数取值范围
2020-09-27陶兴红
陶兴红
(安徽省六安市第二中学,237005)
分类讨论、数形结合和分离参数是求参数取值范围的常规方法,但对指数与对数混合题型,用这三种常规方法很难凑效.此时,若用同构法,先通过变形将原式拆分成结构相同的两个式子,再构造函数,利用函数的单调性便能使问题迎刃而解.
例1设k>0,若存在x>0,使log2x-k·2kx≥0成立,求k的取值范围.
解当x>0时,log2x-k·2kx≥0等价于log2x≥k·2kx,即xlog2x≥kx·2kx,亦即log2x·2log2x≥kx·2kx.
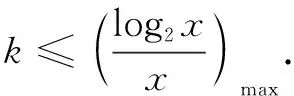
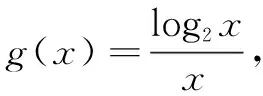
例2已知函数f(x)=ex-aln(ax-a)+a(a>0),若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
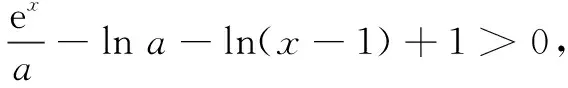
令g(x)=ex+x,易知g(x)在R上单调增,故f(x)>0等价于g(x-lna)>g[ln(x-1)],可得x-lna>ln(x-1),即-lna>ln(x-1)-x.
由常见不等式lnt≤t-1(t>0),得ln(x-1)-x≤x-2-x=-2,所以-lna>-2,即0 例3若对任意x∈(0,+∞),不等式2e2x-alna-alnx≥0恒成立,求a的取值范围. 易知(2x-lnx)min=1+ln 2,故a≤2e.注意到a>0,得a∈(0,2e]. 解法2原不等式可化为2e2x≥alnax,即2xe2x≥(lnax)eln ax. 设g(x)=xex,则g(x)在(0,+∞)单调增.由g(2x)≥g(lnax),得2x≥lnax,即a≤ 解不妨设x1>x2,则由条件可知a≥0,且原不等式等价于f(x1+a)-f(x2+a)>3x1-3x2,即f(x1+a)-3x1>f(x2+a)-3x2在(0,+∞)恒成立. 设g(x)=f(x)-3x,则问题等价于g(x1+a)>g(x2+a)在(0,+∞)恒成立.由x1>x2>0,知x1+a>x2+a>a,于是问题进一步等价于g(x)在(a,+∞)单调增,即g′(x)≥0在(a,+∞)上恒成立. 综上,实数a的取值范围为[2,+∞).