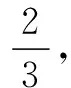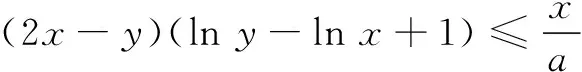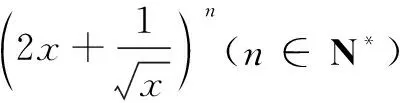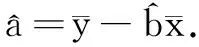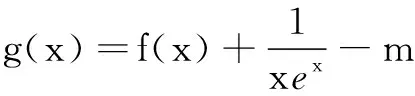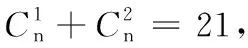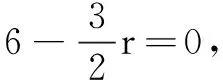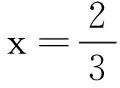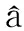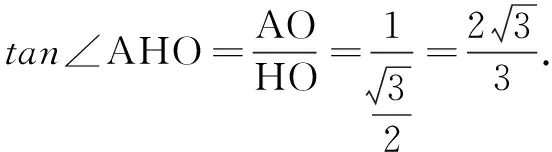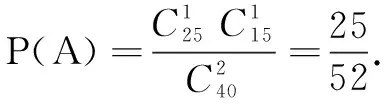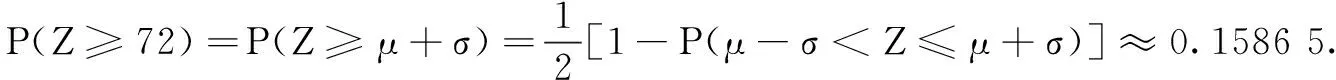高二数学测试

一、单项选择题(本大题共9小题,每小题5分,计45分.在每小题给出的四个选项中,只有一项符合要求)

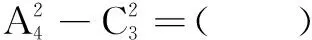
(A) 3 (B)9 (C)12 (D)15

2.下列结论中正确的是( )

(B)若y=(2x+1)3,则y′=3(2x+1)2

(C)若y=x2ex,则y′=2xex

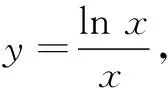
3.将2封不同的信投入3个不同的信箱,不同的投法种数为 ( )

4.若复数z满足z(3-i)=8-6i(i为虚数单位),则z的虚部为 ( )

(A) 1 (B) 3 (C)-1 (D)-3

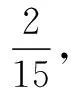
6.为全面贯彻党的教育方针,落实立德树人的根本任务,某学校积极推进教学改革,开发了10门校本课程,其中艺术类课程4门,劳动类课程6门.小明从10门课程中任选3门,则出现艺术类课程的概率为( )

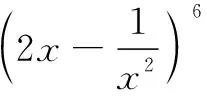
(A)展开式中二项式系数之和为32

(B)展开式中各项系数之和为1

(C)展开式中第3项的二项式系数最大

(D)展开式中系数最大的项为第4项

8.某省新高考方案规定的选科要求为:学生先从物理、历史两科中任选一科,再从化学、生物、政治、地理四门学科中任选两科.现有甲、乙两名学生按上面规定选科,则甲、乙恰有一门学科相同的选科方法有( )种

(A)24 (B)30 (C)48 (D)60

9.若集合A={1,2,3,4},B={1,2,3,4,5},从集合A中任取3个不同的元素,其中最小的元素用a表示,从集合B中任取3个不同的元素,其中最大的元素用b表示,记X=b

二、多项选择题(本大题共3个小题,每小题5分,计15分.在每小题给出的四个选项中有多项符合要求,全部选对的得5分,选对但不全的得3分,有选错的得0分)

10.已知i为虚数单位,则下列选项中正确的是 ( )

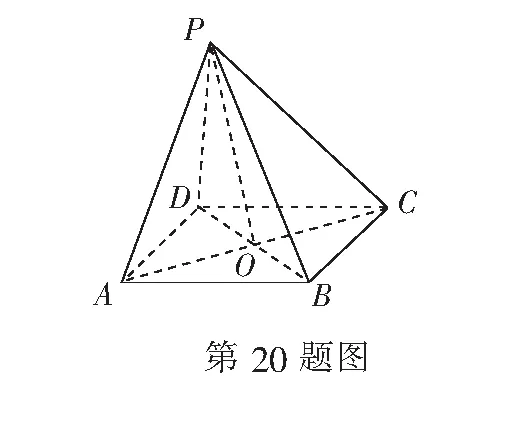
(A)复数z=3+4i的模|z|=5

(C)若复数(m2+3m-4)+(m2-2m-24)i是纯虚数,则m=1或m=-4

(D)对任意的复数z,都有z2≥0

11.已知随机变量ξ的分布列是

ξ-101P121-p2p2

随机变量η的分布列是

η123P121-p2p2

则当p在(0,1)内增大时,下列选项中正确的是( )

(A)E(ξ)=E(η)

(B)V(ξ)=V(η)

(C)E(ξ)增大

(D)V(η)先增大后减小

12.已知函数f(x)=xex,若x1

(A)(x1-x2)]f(x1)-f(x2)]>0

(B)x1f(x2)>x2f(x1)

(D)f(x1)-f(x2)

三、填空题(本大题共4小题,每小题5分,计20分)

13.若随机变量X～N(2,32),且P(X

15.如图,在长方体ABCD-A1B1C1D1中,若AB=2,AD=AA1=1,则点B1到平面D1BC的距离为______.

四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

(1)求n的值;

(2)求展开式中的常数项.

18.(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在点P(1，3)处的切线方程为y=3x,且函数f(x)在x=-2处取得极值.

(1)求f(x)的解析式;

(2)当x∈[-3,1]时，求f(x)的最大值.

19.(本小题满分12分)新冠肺炎疫情防控时期,各级各类学校组织师生开展了“停课不停学”活动.为了解班级线上学习情况,某位班主任老师进行了有关调查研究.

(1)从班级随机选出5名同学,对比研究了线上学习前后两次数学考试成绩,如下表:

线上学习前成绩x1201101009080 线上学习后成绩y145130120105100

求y关于x的线性回归方程;

(2)针对全班45名同学(25名女生,20名男生)的线上学习满意度调查中,女生满意率为80%,男生满意率为75%,填写下表,判断能否在犯错误概率不超过0.01的前提下，认为线上学习满意度与学生性别有关.

满意人数不满意人数合计 男生 女生 合计

参考公式和数据:

20.(本小题满分12分)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,AC∩BD=O,∆PAC为正三角形,AC=2.

(1)求直线PA与平面PBD所成角的大小;

(2)若∠BPO=30°,求二面角A-PB-D的正切值.

21.(本小题满分12分)某市举办了一次“诗词大赛”,分预赛和复赛两个环节.已知共有20 000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下的统计数据.

得分(百分制)[0,20)[20,40)[40,60)[60,80)[80,100]人数1020302515

(1)规定预赛成绩不低于80分为优良,若从样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;

(2)由样本数据分析可知,该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组数据的中间值代替),且σ2=361.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于72分的人数;

(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:

① 参加复赛的学生初始分都设置为100分；

② 参加复赛的学生可在答题前自己决定答题数量n,每一题都需要“花”掉一定分数来获取答题资格(即用分数来买答题资格),规定答第k题时“花”掉的分数为0.2k(k=1,2,…n);

③ 每答对一题得2分，答错得0分；

④ 答完n题后参赛学生的最终分数即为复赛成绩.

已知学生甲答对每道题的概率均为0.75,且每题答对与否都相互独立.若学生甲希望获得最佳的复赛成绩,则他的答题数量n应为多少?

参考数据:若Z～N(μ,σ2),则P(μ-σ

(1)若b=0,求f(x)的单调区间;

参考答案

一、单项选择题

1.B；2.D；3.C；4.C；5.C；6.A；

7.B；8.D；9.A；

二、多项选择题

10.AB； 11.BC； 12.BCD.

三、填空题

四、解答题

18.(1)f′(x)=3x2+2ax+b,由题意得

解得a=2,b=-4,c=4.故f(x)=x3+2x2-4x+4,经检验符合要求.

=1.15，

=5.

所求线性回归方程为y=1.15x+5.

(2)列表如下:

满意人数不满意人数合计 男生15520 女生20525 合计351045

H0:假设学生线上学习满意度与学生性别无关,计算得

因为K2≈0.161<6.635，所以在犯错误概率不超过0.01的前提下，不可以认为线上学习满意度与学生性别有关.

20.因为四边形ABCD是菱形,所以AC⊥BD,且O是AC,BD的中点.

(1) 因为AC⊥BD,AC⊥PO,PO⊂平面PBD,BD⊂平面PBD,PO∩BD=O,所以AC⊥平面PBD.

所以PO为PA在平面PBD内的射影,∠APO即为直线PA与平面PBD所成的角.

在正三角形PAC中,PO是AC边上的中线,所以∠APO=30°.

因为AO⊥平面PBD,PB⊂平面PBD,所以AO⊥PB.

又AO∩OH=O,AO⊂平面AOH,HO⊂平面AOH,所以PB⊥平面AOH.

因为AH⊂平面AOH,所以PB⊥AH；又OH⊥PB,所以∠AHO即为所求二面角A-PB-D的平面角.

所以，全市参加参赛的全体学生中成绩不低于72分的人数大约为20 000×0.158 65=3 173.

(3)以随机变量ξ表示甲答对的题数,则ξ～B(n,0.75),且Eξ=0.75n.

记甲答完n题所加的分数为随机变量X,则X=2ξ,EX=2Eξ=1.5n.

依题意，为了获取答n题的资格,甲需要“花”掉的分数为0.2×(1+2+3+…+n)=0.1(n2+n).

设甲答完n题的分数为f(n),则f(n)=100-0.1(n2+n)+1.5n=-0.1(n-7)2+104.9.

由于n∈N*,故当n=7时,f(n)取最大值104.9,即复赛成绩的最大值为104.9.

所以，若学生甲期望获得最佳复赛成绩,则他的答题量n应该是7.

当a≤0时，f′(x)>0,f(x)在(0,+∞)单调增；当a>0时，f(x)在(0,a)单调减，在(a,+∞)单调增.

又x0ex0=1，得ln(x0ex0)=0，即lnx0+x0=0,故g(x0)=1-m.由g(x)有且只有2个零点，得g(x0)=1-m<0,即m>1.

下面用零点存在性定理证明：当m>1时，函数g(x)有且只有2个零点.

令φ(m)=em-2m(m>1),则φ′(m)=em-2>0,φ(m)在(1,+∞)单调增，得φ(m)>φ(1)=e-2>0.

又g(x0)=1-m<0,g(x)在(0,x0)连续且单调减，故g(x)在(0,x0)有且只有1个零点.

综上，得m>1.